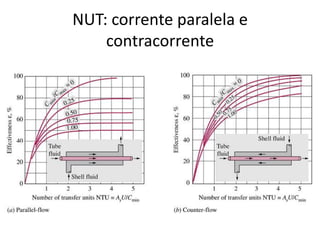
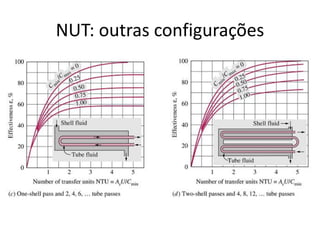
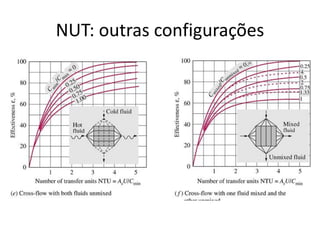
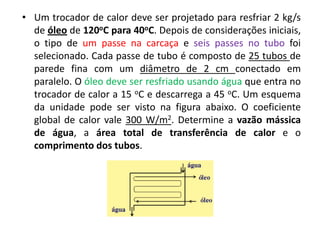
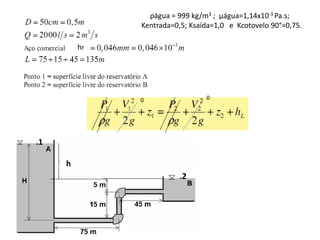
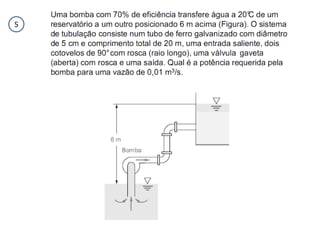
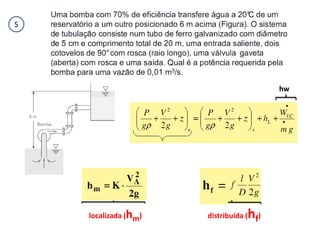
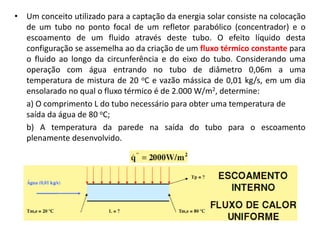
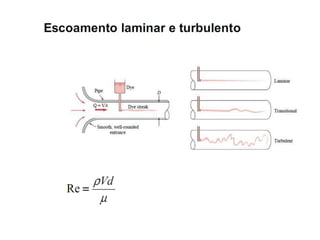
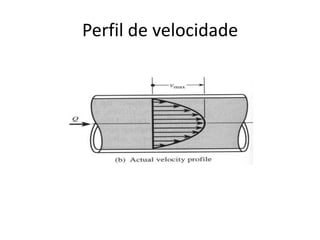
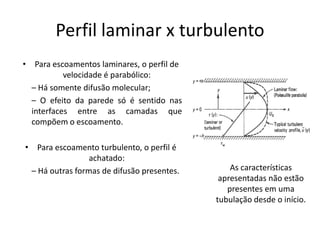
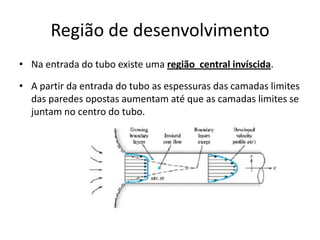
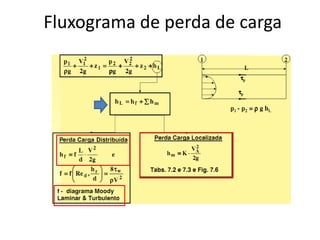
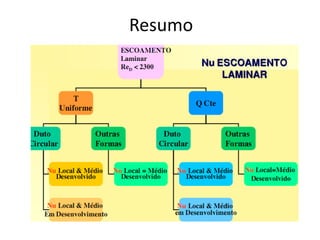
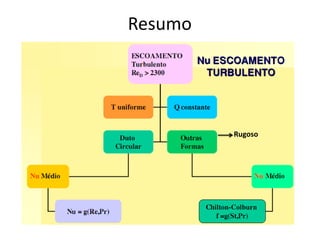
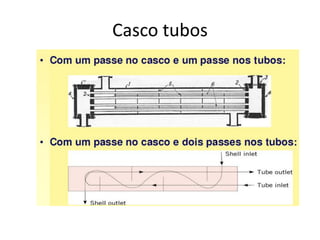
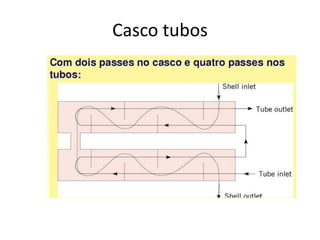
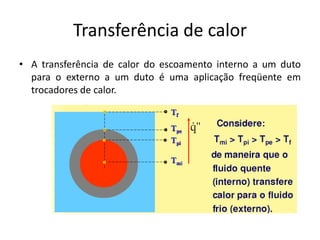
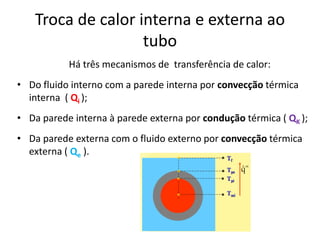
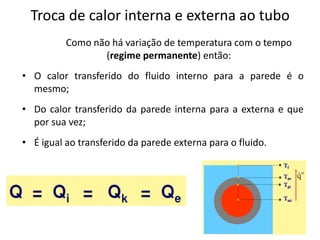
O capítulo resume os principais conceitos do escoamento interno de fluidos em tubulações, incluindo o perfil de velocidade laminar e turbulento, o desenvolvimento do escoamento, a perda de carga distribuída e localizada, e a transferência de calor entre o fluido e a parede da tubulação.





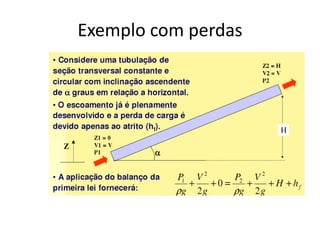


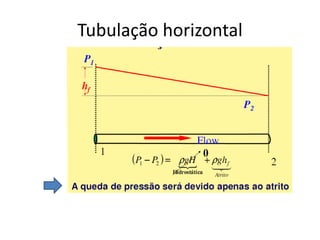
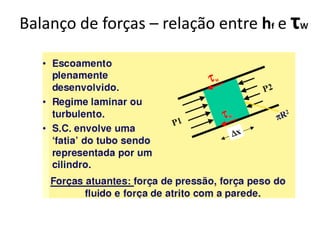
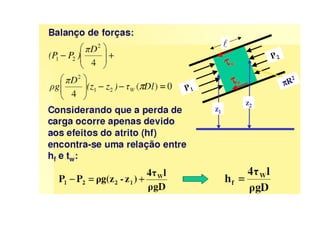























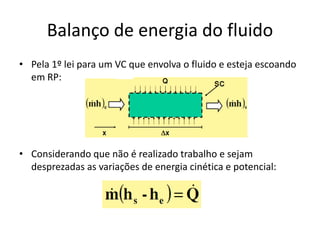



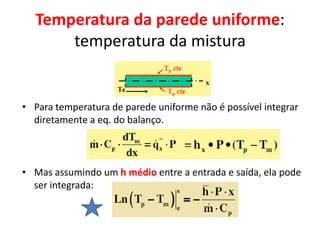
























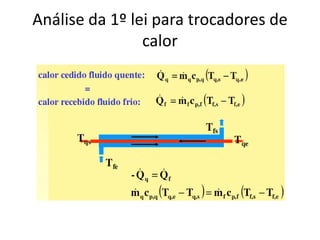
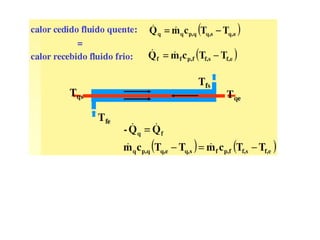
![Análise da 1º lei para trocadores de
calor
• O produto da vazão mássica com o calor específico é conhecido
como Capacidade Térmica do fluxo de fluido - C [W/ºC]:
Fluido quente está perdendo calor.](https://image.slidesharecdn.com/captulo7-111026071939-phpapp02/85/Capitulo-7-113-320.jpg)