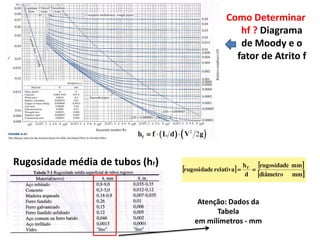
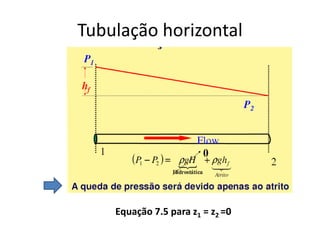
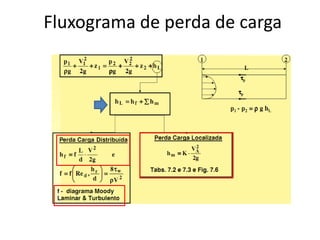
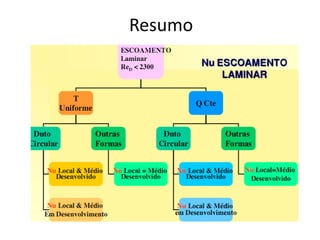
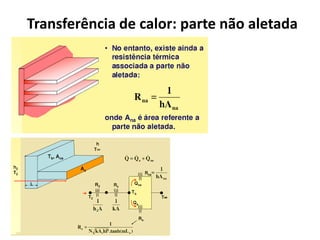
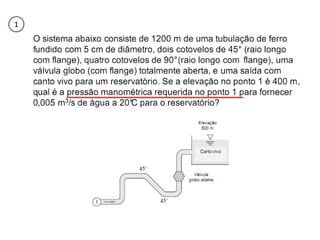
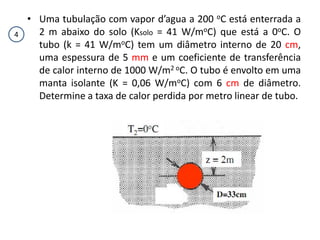
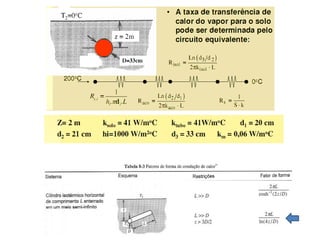
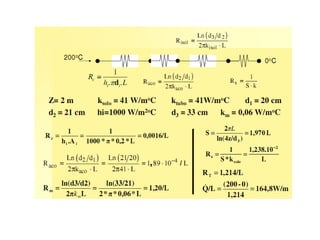
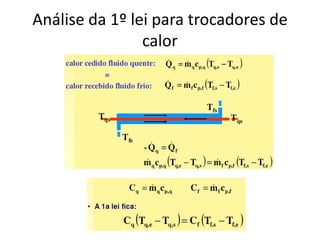
O documento discute escoamento interno de fluidos, perda de carga em tubulações e trocadores de calor. Ele descreve como calcular perda de carga considerando atrito, como determinar taxa de transferência de calor em aletas e a importância do número de unidades térmicas e da efetividade para o projeto de trocadores.

1. Revisão e Exercícios P3

2. Escoamento interno
• O fluido está completamente confinado por uma superfície
sólida.
• Representa o escoamento de um fluido em um duto ou tubo.
• Assim como no escoamento externo, no interno há dois
regimes distintos: Recr = 2300
– Laminar: Re < 2300
– Turbulento: Re > 2300
• Nesse caso o número de Reynolds é ligeiramente distinto,
sendo definido como:
Sendo “D” o diâmetro
interno do tubo

3. Perda de carga (hL)
• Representa as perdas irreversíveis de energia do escoamento:
– Quando o fluido se dirige de um ponto ao outro da tubulação.
• Sua origem é o atrito que a parede da tubulação exerce sobre o
fluido.
• Reflete em uma variação de pressão ao longo do escoamento.
• A perda de carga pode estar distribuída (hf) ao longo de toda
tubulação e/ou localizada (hm) em um acessório (curva, restrição,
válvula, etc):
localizada (hm) h
distribuída ( f)

4. Como Determinar
hf ? Diagrama
de Moody e o
fator de Atrito f
Rugosidade média de tubos (hr)
Atenção: Dados da
Tabela
em milímetros - mm

5. Tubulação horizontal
Equação 7.5 para z1 = z2 =0

6. Fluxograma de perda de carga

7. Resumo

8. Resumo

9. Resumo
Rugoso

10. Condução de calor unidimensional em RP
• O fluxo de calor pode ser calculado através da Lei de Fourier
como:
Fluxo de
Calor

12. Condução de calor unidimensional em RP
• No caso de parede compostas, o conceito de resistência
térmica pode ser utilizado de forma análoga a circuitos
elétricos série/paralelo

13. Resumo
(Isolante)

14. Aleta finita e ponta isolada
• Analisando através do circuito térmico, a resistência térmica
da aleta:
onde N é o número de aletas
fixadas à superfície.
• A taxa de transferência de calor da aleta pode ser
determinado como:
• Onde:

15. Transferência de calor: aleta finita e
condição de convecção
• Caso exista uma condição de contorno de convecção na
extremidade da aleta (com transferência de calor para o
ambiente, por exemplo), o comprimento da aleta precisa ser
alterado:
• Para o caso de uma aleta cilíndrica com diâmetro D, a correção
do comprimento da aleta será:
• Este novo comprimento de aleta (Lc) será usado no cálculo da
resistência térmica da aleta:

16. Transferência de calor: parte não aletada

17. Fator de forma de condução
• Considerando que a geometria contém somente DUAS superfícies
ISOTÉRMICAS, T1 e T2, e que o material é homogêneo:
• Onde S é o fator de forma de condução e tem dimensão de
comprimento (m).
• Comparando esta equação com a das placas planas infinitas
(unidimensional) pode-se determinar que o seu fator de forma de
condução é:
Tabela 8-3.
Páginas 312 a 314

18. Resumo: Condução Transiente
• Bi <0,1 Análise Concentrada: “Corpo qualquer”
• Unidimensional. Bi>0,1 Sólido semi-infinito: 3
condições de contorno (Mudanças súbitas em: Ts, Q,
T): “Fórmulas erf (X)”
• Unidimensional. Bi>0,1 Placa infinita , Cilindro
Infinito: “Gráficos” Lc = L/2
• Configurações multidimensionais:
“Produto das Tadimensionais” Lc = L

19. 1

21. 2

24. .
Q

26. • Uma tubulação com vapor d’agua a 200 oC está enterrada a
4 2 m abaixo do solo (Ksolo = 41 W/moC) que está a 0oC. O
tubo (k = 41 W/moC) tem um diâmetro interno de 20 cm,
uma espessura de 5 mm e um coeficiente de transferência
de calor interno de 1000 W/m2 oC. O tubo é envolto em uma
manta isolante (K = 0,06 W/moC) com 6 cm de diâmetro.
Determine a taxa de calor perdida por metro linear de tubo.

30. Tc=49,04oC

31. • Um processo para tratamento de um material especial deve ser avaliado. O
material, uma esfera com raio 5 mm, encontra-se inicialmente em equilíbrio a
400 oC no interior de um forno. O material é repentinamente removido do forno e
submetido a um processo de resfriamento em duas etapas.
Etapa1: resfriamento ano ar a 20oC (ha = 10 W/m2 K) por um período de tempo
ta até que a temperatura do centro atinja um valor crítico igual a 335oC.
Etapa 2: Resfriamento em um banho agitado de água a 20oC e hb = 600 W/m2 K.
1. Calcule o tempo requerido para a Etapa 1 do processo de resfriamento se
completar (ta).
2. Calcule o tempo requerido para a Etapa 2 do processo (tb), para que o centro da
esfera se resfriar de 335oC (condição final da Etapa 1) para 50oC.
As propriedades termofísicas do material são:
20 3000 1000
6,66

32. 1 Lc = V/A = r/3
Bi= h x Lc / k = 10 x 0.005 / 3 x 20 = 8,33 x 10 -4 < 0,1
t = 3000 x 0,005 x 1000 x ln (400-20/335-20)
t = 94s
2
Bi= h x Lc / k = 6000 x 0.005 / 3 x 20 = 0,5 > 0,1
Portanto não pode usar o método da Capacitância Global.
Problema sem solução.

33. Análise da 1º lei para trocadores de
calor

34. Método da efetividade (ε)
• A efetividade de um trocador de calor é a razão entre a taxa
de calor que ele troca pela máxima taxa de calor que ele
pode trocar:
• onde Q max é igual ao produto da menor capacidade térmica
entre os dois fluidos pela máxima diferença de temperatura
possível no trocador de calor (entrada):

35. Como calcular a efetividade
• A efetividade de um trocador é uma função:
• 1. do Número de Unidades Térmicas:
• 2. da razão entre Capacidades Térmicas:
• 3. da Configuração do Trocador.
* NTU: representa um índice da
Gráficos 7.21 a 7.26 dimensão do trocador.
No projeto de um trocador de calor é
necessário estabelecer condições que
resultam em valores moderados de
NTU, de modo a não subdimensionar
nem superdimensionar o
equipamento.