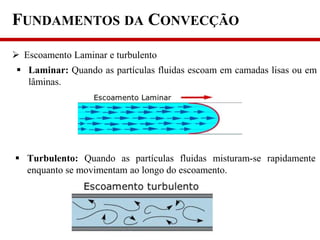
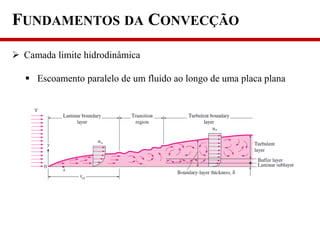
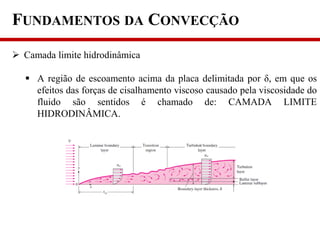
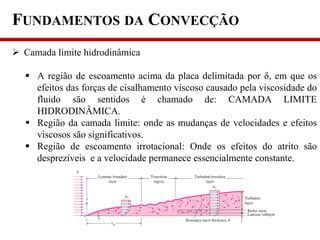
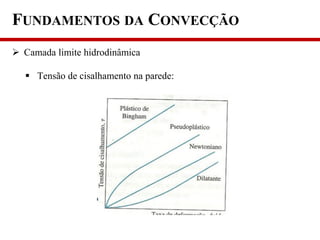
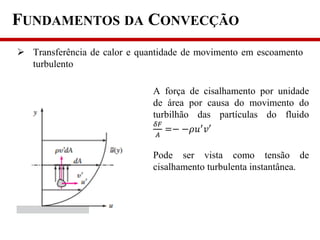
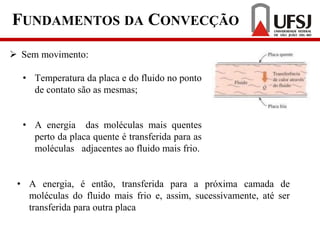
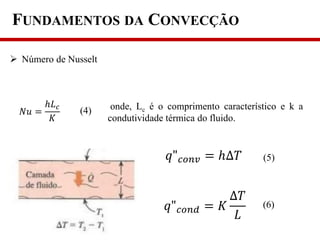
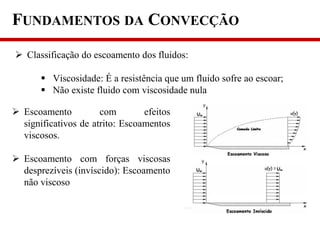
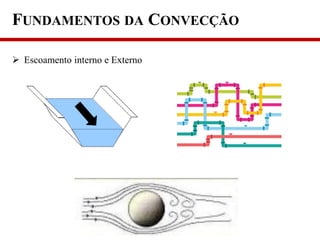
1) O documento discute os fundamentos da convecção, incluindo os mecanismos de transferência de calor, classificação da convecção e propriedades que afetam a taxa de transferência de calor; 2) A convecção ocorre quando um fluido está em movimento e transfere calor, diferente da condução que ocorre em fluidos estagnados; 3) A taxa de transferência de calor depende de propriedades do fluido e da velocidade, geometria, tipo de escoamento e diferença de temperatura.

1. FUNDAMENTOS DA CONVECÇÃO

2. FUNDAMENTOS DA CONVECÇÃO
 Mecanismos de transferência de calor:
• Condução
• Convecção
• Radiação
Transferência de calor através de um sólido: Condução
Transferência de calor através de um líquido ou um gás:
Em movimento - convecção
Sem movimento - condução
Semelhantes

3.  Classificação da convecção:
• Convecção forçada: O fluido é forçado a escoar sobre a superfície ou
dentro de um tubo por meios externos, como um ventilador ou uma
bomba.
• Convecção Natural: Qualquer movimento do fluido é causado por
meios naturais como o efeito do empuxo, que se manifesta com
fluidos quentes subindo e fluidos frios descendo.
• Convecção Externa: O fluido escoa sobre uma superfície.
• Convecção interna: O fluido escoa dentro de um tubo.
FUNDAMENTOS DA CONVECÇÃO

4.  Sem movimento:
• Temperatura da placa e do fluido no ponto
de contato são as mesmas;
• A energia das moléculas mais quentes
perto da placa quente é transferida para as
moléculas adjacentes ao fluido mais frio.
FUNDAMENTOS DA CONVECÇÃO
• A energia, é então, transferida para a próxima camada de
moléculas do fluido mais frio e, assim, sucessivamente, até ser
transferida para outra placa

5. FUNDAMENTOS DA CONVECÇÃO
 A T. de calor por convecção depende fortemente das:
 Propriedades do Fluido.
 Viscosidade dinâmica;
 Condutividade térmica;
 Massa específica;
 Calor específico;
 Da velocidade do fluido.
 Da geometria e rugosidade do sólido.
 Do tipo de escoamento do fluido.
 Laminar;
 Turbulento

6.  Proporcional a diferença de temperatura;
 Lei de resfriamento:
𝑞 = ℎ 𝑇𝑠 − 𝑇∞ (W/m2) (1)
𝑄 = ℎ𝐴 𝑇𝑠 − 𝑇∞ (W) (2)
FUNDAMENTOS DA CONVECÇÃO

7.  A propriedade do fluido responsável pela condição de não deslizamento
e pelo desenvolvimento da camada limite é a viscosidade.
 Outra condição de não deslizamento é o arrasto na superfície.
FUNDAMENTOS DA CONVECÇÃO

8.  A implicação da condição de não deslizamento é que a transferência de
calor a partir de uma superfície sólida para a camada de fluido adjacente
à superfície ocorre por condução pura.
𝑞 𝑐𝑜𝑛𝑣 = 𝑞 𝑐𝑜𝑛𝑑 = −𝐾𝐹𝑙𝑢𝑖
𝑑𝑇
𝑑𝑦
y=0
(W/m2) (2)
 Igualando Eq. (1) e (2):
ℎ =
−𝐾 𝑓𝑙𝑢𝑖 𝑑𝑇 𝑑𝑦 𝑦=0
𝑇𝑠−𝑇∞
(W/m2.K) (3)
FUNDAMENTOS DA CONVECÇÃO

9. onde, Lc é o comprimento característico e k a
condutividade térmica do fluido.
(4)𝑁𝑢 =
ℎ𝐿 𝑐
𝐾
𝑞" 𝑐𝑜𝑛𝑣 = ℎ∆𝑇
𝑞" 𝑐𝑜𝑛𝑑 = 𝐾
∆𝑇
𝐿
(5)
(6)
FUNDAMENTOS DA CONVECÇÃO
 Número de Nusselt

10.  O n° de Nusselt representa o aumento da transferência de calor através da
camada de fluido como resultado da convecção em relação à condução
do mesmo fluido em toda camada.
 Quanto maior o n° de Nulsselt, mais eficaz será a convecção. Para Nu=1
a transferência de calor é por condução pura.
𝑞" 𝑐𝑜𝑛𝑣
𝑞" 𝑐𝑜𝑛𝑑
=
ℎ∆𝑇
𝑘∆𝑇/𝐿
=
ℎ𝐿
𝐾
= 𝑁𝑢 (7)
FUNDAMENTOS DA CONVECÇÃO

11. FUNDAMENTOS DA CONVECÇÃO
Exemplo: Durante um fluxo de ar
𝑇∞ = 20 °𝐶 sobre a superfície de uma
placa mantida a uma temperatura de
𝑇𝑠 = 160 °𝐶, o perfil de temperatura
adimensional dentro da camada de ar
sobre a placa está determinado para
ser:
𝑇(𝑦) − 𝑇∞
𝑇𝑠 − 𝑇∞
= 𝑒−𝑎𝑦
Na qual a = 3200 m-1 e y é a distância vertical medida a partir da superfície
da placa em m. determine o fluxo de calor na superfície da placa e o
coeficiente de transferência de calor por convecção.

12. FUNDAMENTOS DA CONVECÇÃO
 Classificação do escoamento dos fluidos:
 Viscosidade: É a resistência que um fluido sofre ao escoar;
 Não existe fluido com viscosidade nula
 Escoamento com efeitos
significativos de atrito: Escoamentos
viscosos.
 Escoamento com forças viscosas
desprezíveis (invíscido): Escoamento
não viscoso

13. FUNDAMENTOS DA CONVECÇÃO
 Escoamento interno e Externo

14. FUNDAMENTOS DA CONVECÇÃO
 Compressível: Há variação da massa específica ao longo do
escoamento, é muito comum com gases.
 Incompressível: Não Há variação da massa específica, ocorre
com a maioria dos líquidos
 Escoamento Compressível e Incompressível

15. FUNDAMENTOS DA CONVECÇÃO
 Escoamento Laminar e turbulento
 Laminar: Quando as partículas fluidas escoam em camadas lisas ou em
lâminas.
 Turbulento: Quando as partículas fluidas misturam-se rapidamente
enquanto se movimentam ao longo do escoamento.

16. FUNDAMENTOS DA CONVECÇÃO
 Escoamento Laminar e turbulento
 O regime de escoamento, se laminar ou turbulento, é determinado pela
seguinte quantidade adimensional, chamada de número de Reynolds:
𝑅 𝑒 =
𝜌𝑣 𝑑
𝜇
Onde:
𝜇 = viscosidade
d = diâmetro
v = velocidade
Re < 2300 (R. Laminar)
2000 < Re < 2300 (Transição)
Re > 2300 (R. Turbulento)
* Verificar no livro

17. FUNDAMENTOS DA CONVECÇÃO
 Escoamento Natural e forçado
 Escoamento forçado utiliza bombas
 Escoamento natural, ocorre por meios naturais. Como por exemplo
correntes convectivas.

18. FUNDAMENTOS DA CONVECÇÃO
 Escoamento Regime permanente e Regime não-permanente
 Regime permanente: as propriedade do escoamento não variam com o
tempo.
 Regime não permanente: as propriedades do escoamento variam com o
tempo.
𝑑𝑛
𝑑𝑡
= 0
𝑑𝑛
𝑑𝑡
≠ 0

19. FUNDAMENTOS DA CONVECÇÃO
 Escoamentos uni, bi e tridimensionais
 Escoamento uni, bi e tridimensional varia a velocidade em um, duas e
três dimensões respectivamente.
 V (x, y, z): Coordenadas cartesianas
 V(r,𝜃, z): Coordenadas cilíndricas

20. FUNDAMENTOS DA CONVECÇÃO
 Camada limite hidrodinâmica
 Escoamento paralelo de um fluido ao longo de uma placa plana

21. FUNDAMENTOS DA CONVECÇÃO
 Camada limite hidrodinâmica
 As velocidades das partículas do fluido da primeira camada adjacente à
placa torna-se nula em virtude da condição de não deslizamento
 A presença da placa é sentida até alguma distância normal δ a partir da
placa.
 O componente x da velocidade U varia de 0 em y=0 para quase v em
y= δ

22. FUNDAMENTOS DA CONVECÇÃO
 Camada limite hidrodinâmica
 A região de escoamento acima da placa delimitada por δ, em que os
efeitos das forças de cisalhamento viscoso causado pela viscosidade do
fluido são sentidos é chamado de: CAMADA LIMITE
HIDRODINÂMICA.

23. FUNDAMENTOS DA CONVECÇÃO
 Camada limite hidrodinâmica
 A região de escoamento acima da placa delimitada por δ, em que os
efeitos das forças de cisalhamento viscoso causado pela viscosidade do
fluido são sentidos é chamado de: CAMADA LIMITE
HIDRODINÂMICA.
 Região da camada limite: onde as mudanças de velocidades e efeitos
viscosos são significativos.
 Região de escoamento irrotacional: Onde os efeitos do atrito são
desprezíveis e a velocidade permanece essencialmente constante.

24. FUNDAMENTOS DA CONVECÇÃO
 Camada limite hidrodinâmica
 Tensão de cisalhamento na parede:

25. FUNDAMENTOS DA CONVECÇÃO
 Camada limite hidrodinâmica
 Tensão de cisalhamento na parede:

26. FUNDAMENTOS DA CONVECÇÃO
 Camada limite Térmica

27. FUNDAMENTOS DA CONVECÇÃO
 Número de Prandtl :
A espessura relativa das camadas limite hidrodinâmica e térmica é mais
bem descrita pelo parâmetro adimensional número de Prandtl

28. FUNDAMENTOS DA CONVECÇÃO
 Número de Prandtl :
O número de Pr para gases é cerca de 1, o que indica que tanto a
quantidade de movimento quanto o calor dissipam-se através do fluido
mais ou menos na mesma taxa.
O calor se difunde muito rapidamente em metais líquidos (Pr ≪ 1) e
muito lentamente em óleos (Pr ≫1) em relação a quantidade de
movimento.

29. FUNDAMENTOS DA CONVECÇÃO
 Transferência de calor e quantidade de movimento em escoamento
turbulento
Os escoamentos permanentes são caracterizados por flutuações caóticas
e rápidas nas regiões de redemoinhos do fluido ao longo do escoamento,
chamadas turbilhões.
Mesmo quando o escoamento médio é permanente, o movimento dos
turbilhões em escoamentos turbulentos causam flutuações significativas
nos valores de V, T, P, e ate mesmo na μ (quando escoamento
compressível).

30. FUNDAMENTOS DA CONVECÇÃO
 Transferência de calor e quantidade de movimento em escoamento
turbulento
A força de cisalhamento por unidade
de área por causa do movimento do
turbilhão das partículas do fluido
𝛿𝐹
𝐴
=− −𝜌𝑢′ 𝑣′
Pode ser vista como tensão de
cisalhamento turbulenta instantânea.

31. FUNDAMENTOS DA CONVECÇÃO
 Transferência de calor e quantidade de movimento em escoamento
turbulento
A tensão de cisalhamento turbulento é definida como:
𝜏 𝑡𝑢𝑟 = −𝜌𝑢′ 𝑣′ = 𝜇 𝑡
𝑑𝑢
𝑑𝑦
e 𝑞𝑡𝑢𝑟 = 𝜌𝐶 𝑝 𝑣𝑇 = −𝐾𝑡
𝑑𝑇
𝑑𝑌
Onde : 𝜇 𝑡 é chamada viscosidade turbulenta, 𝐾𝑡 é chamada
condutividade térmica turbulenta.

32. FUNDAMENTOS DA CONVECÇÃO
 Transferência de calor e quantidade de movimento em escoamento
turbulento
Assim a tensão de cisalhamento e fluxo total de calor pode ser expresso
como:
Onde: 𝑣 𝑡 = 𝜇 𝑡/𝜌 é a viscosidade cinemática de turbilhão, e 𝛼 𝑡 = 𝐾𝑡/𝜌 é
a difusividade térmica do turbilhão.
𝜏 𝑡𝑜𝑡𝑎𝑘 = 𝜇 − 𝜇 𝑡
𝑑𝑢
𝑑𝑦
= ρ(𝑣 − 𝑣 𝑡)
𝑑𝑢
𝑑𝑦
𝑞𝑡𝑜𝑡𝑎𝑙 = − 𝐾 + 𝐾𝑡
𝑑𝑇
𝑑𝑌
= −𝜌𝐶 𝑝(𝛼 − 𝛼 𝑡) = −𝐾𝑡
𝑑𝑇
𝑑𝑌

33. FUNDAMENTOS DA CONVECÇÃO
 Equação da continuidade:
Essa é a conservação da massa em forma diferencial, que também é
conhecida como equação da continuidade ou balanço de massa para
escoamento permanente bidimensional de fluido com densidade
constante
Taxa defluxo de massa
entrando no volume de
controle
Taxa de fluxo de massa
saindo do volume de
controle
𝑑𝑢
𝑑𝑥
+
𝑑𝑣
𝑑𝑦
= 0

34. FUNDAMENTOS DA CONVECÇÃO
 Equação da continuidade de movimento:
Este é o balanço da quantidade de movimento na direção de x, e é
conhecido como equação da quantidade de movimento em x.
Aceleração na
velocidade
especificada
Força líquida (corpo e
superfície) atuando na
mesma direção
𝜌 𝑢
𝑑𝑢
𝑑𝑥
+ 𝑢
𝑑𝑣
𝑑𝑦
= 𝜇
𝑑2
𝑢
𝑑𝑦2 +
𝑑𝑃
𝑑𝑥
Massa

35. FUNDAMENTOS DA CONVECÇÃO
 Equação de conservação da energia:
Estabelece que a energia líquida transportada por convecção pelo fluido
fora do volume de controle é igual à energia líquida transferida para o
volume de controle por condução de calor.
𝜌𝐶 𝑝 𝑢
𝑑𝑇
𝑑𝑥
+ 𝑢
𝑑𝑇
𝑑𝑦
= 𝜇
𝑑2
𝑇
𝑑𝑥2 +
𝑑2
𝑇
𝑑𝑦2
𝐸𝑒𝑛𝑡𝑟𝑎 − 𝐸𝑠𝑎𝑖 = ∆𝐸𝑠𝑖𝑠𝑡𝑒𝑚𝑎