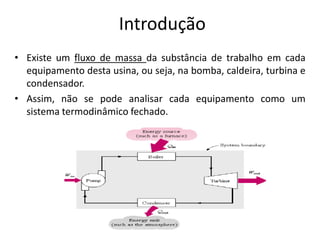
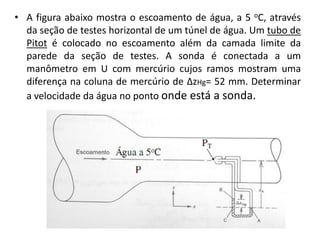
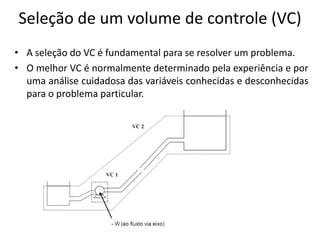
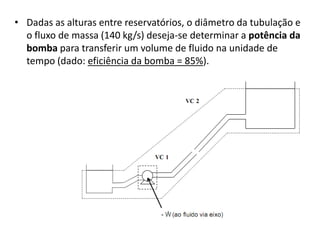
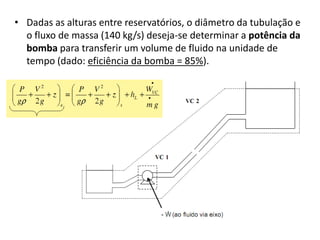
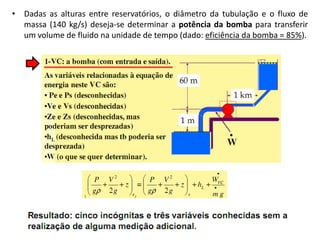
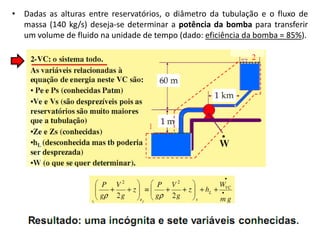
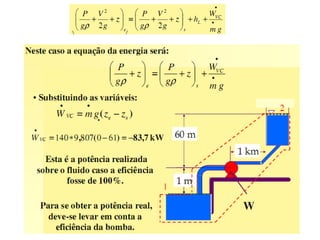
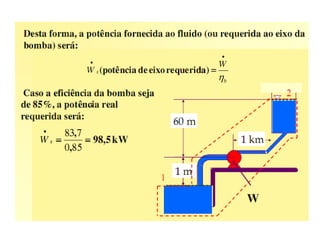
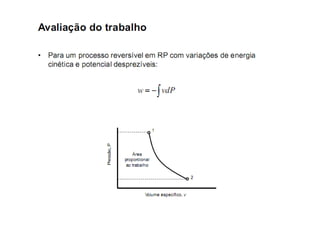
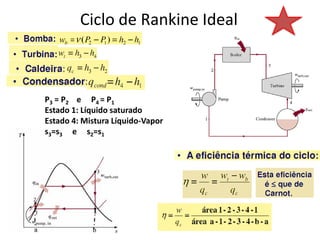
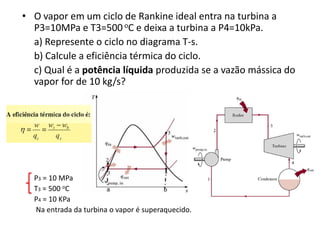
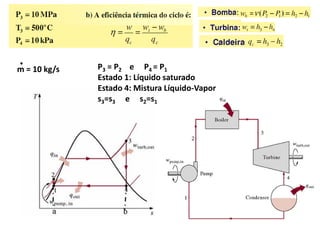
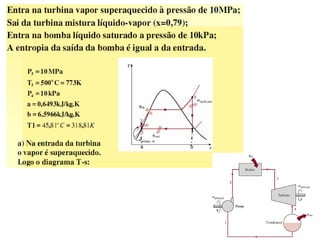
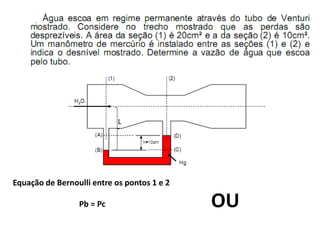
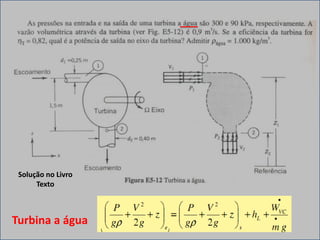
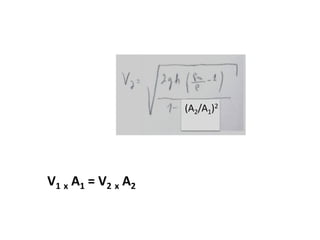Este documento discute conceitos fundamentais de análise termodinâmica através de volume de controle, incluindo:
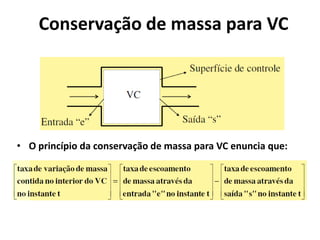
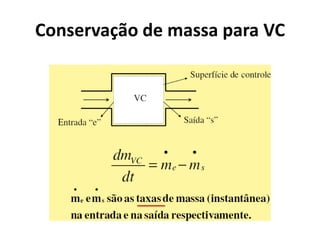
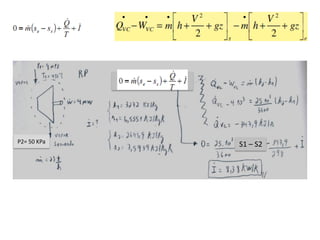
1) O princípio da conservação de massa aplicado a volumes de controle com múltiplas entradas e saídas de fluxo de massa.
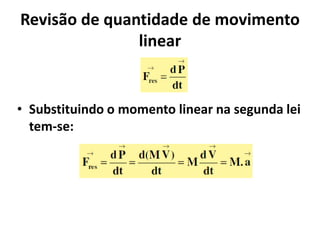
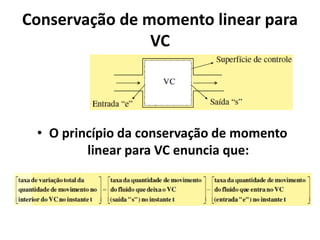
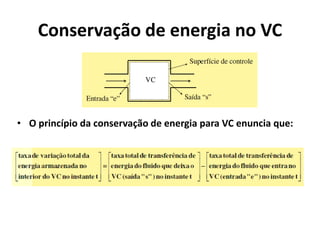
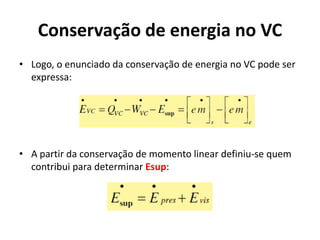
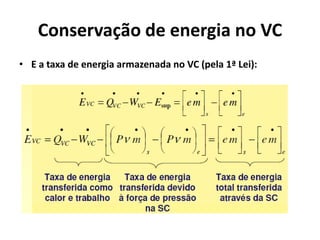
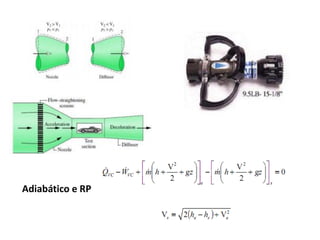
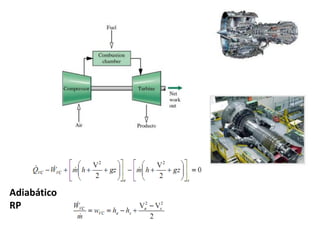
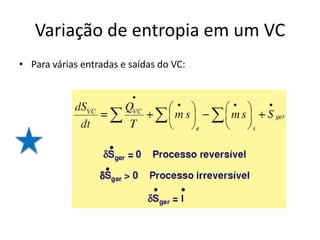
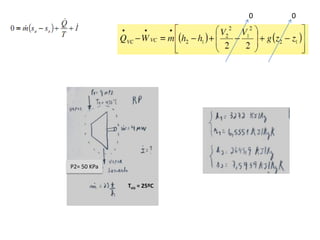
2) Os princípios da conservação da quantidade de movimento e da energia aplicados a volumes de controle, levando em conta forças externas e fluxo de massa, energia e momento.
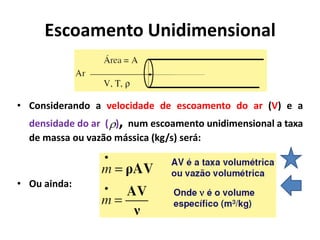
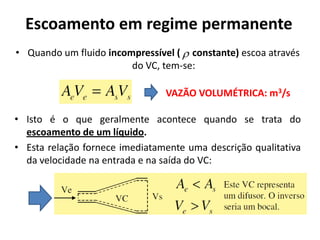
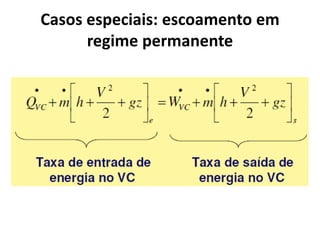
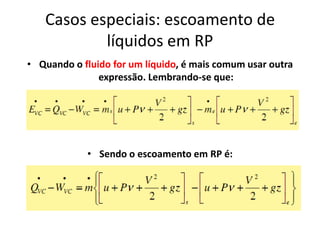
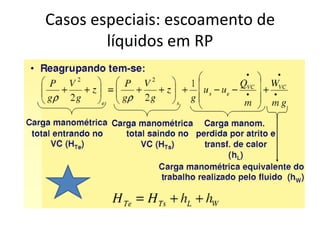
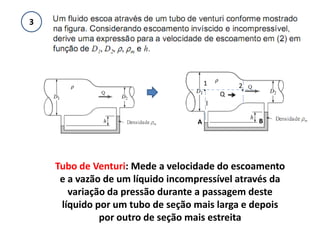
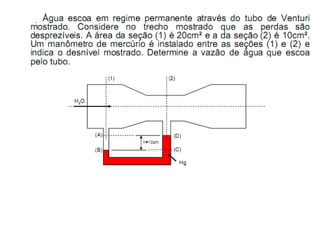
3) Os conceitos de escoamento permanente, pressão, força viscosa e suas