Este documento apresenta o plano de aula para o curso de Física 2 sobre Fluidos ministrado pelo professor Dr. Walmor Cardoso Godoi na UTFPR. O plano inclui tópicos como densidade, pressão, fluidos em repouso, princípios de Pascal e Arquimedes, equações da continuidade e de Bernoulli e suas aplicações.

1. Física 2
Fluidos
Prof. Dr. Walmor Cardoso Godoi
Departamento de Física - DAFIS
Universidade Tecnológica Federal do Paraná – UTFPR
URL: http://dafis.ct.utfpr.edu.br/~godoi
E-mail: walmorgodoi@utfpr.edu.br

2. Agenda
•
•
•
•
•
•
•
•
•
•
O que é um fluido?
Densidade
Pressão
Fluidos em repouso
Medidores de pressão
Princípio de Pascal
Princípio de Arquimedes
Fluidos ideais
A equação da continuidade
A equação de Bernoulli
Referência: Fundamentos de
Física Halliday & Resnick,
Cap 14 - Fluidos, 9ª Edição,
ed. LTC, 2012.

3. Introdução
• Tubulações -> engenharia civil
• Vazão de um rio -> engenharia ambiental
• Flaps de um avião -> engenharia
aeronáutica

4. molinete

5. Hemodinâmica -> bioengenharia
MODELO PRESSÃO
ARTÉRIO - VENOSA
http://www2.ufpa.br/ensinofts/capitulo1.html

6. Trânsito urbano (?)
1. Modelagem do fluxo de pedestres pela teoria
macroscópica, Rev. Bras. Ensino Fís. vol.34 no.4 São Paulo Oct./Dec. 2012
2. B.S. Kerner, The Physics of Traffic (Springer, New York and Berlin,
2004).

7. O que é física de fluidos?
• A mecânica dos fluidos é a parte da física
que estuda o efeito de forças em fluidos.
• Os fluidos em equilíbrio estático são
estudados pela hidrostática e os fluidos
sujeitos a forças externas diferentes de
zero são estudados pela hidrodinâmica.

8. O que é um fluido?
“Um fluido é uma substância que pode
escoar.”
• Os fluidos se amoldam aos contornos de
qualquer recipiente onde colocamos. Eles
fazem isso porque não suportam forças
tangenciais a sua superfície (tensão de
F
cisalhamento).

9. Quais fluidos estudamos?
Estes não....

10. Líquidos e Gases
• Gás
– Ordem: Sistema desordenado (posição e
movimento das partículas)
– Baixa densidade
– Preenchem todo recipiente onde são colocados
– Fácil expansão e compressão

11. Líquidos e Gases
• Líquido
– Ordem: pouco alcance, moléculas e átomos
vizinhos distribuem-se igualmente
– Alta densidade
– Tomam a forma do recipiente onde são
colocados
– Difícil expansão e compressão

12. Líquidos e Gases
• Sólido
– Ordem: longo alcance -> cristais
– Alta densidade
– Não tomam a forma do recipiente onde são
colocados

13. Massa Específica
Massa Específica ( ou Densidade Absoluta)
Massa Esp. uniforme
(corpo homogêneo)
: Massa Específica (kg/m3)
m: Massa (kg)
V: Volume (m3)
H2O-> Densidade à temperatura de 25 °C, é de 1,00 g/cm³, e a
4 °C, onde se atinge sua densidade máxima, é de 1,03 g/cm³

14. 10x
(kg/m3)
1000x
gases
líquido
Ar
1,21 kg/m3 (20ºC, 1 atm)
60,5 kg/m3 (20ºC, 50 atm)
Água
998 kg/m3 (20ºC, 1 atm)
1000 kg/m3 (20ºC, 50 atm)
Argônio 1,784 kg/m3
Argônio 1390 kg/m3
sólido
Gelo 917 kg/m3
Ferro 7900 kg/m3
Chumbo 11340 kg/m3

15. Densímetro

16. Massa Específica

17. Pressão
Força uniforme em uma sup. plana
p: Pressão (Pa= 1 N/m2)
F: Força (N)
A: Área (m2)

18. Pressão
Pressão (Pa)
Centro do Sol
2 x 1016
Salto alto em uma pista de dança
106
Maior pressão em laboratório
1,5 x 1010
Pneu de automóvel
2 x 105 (29 psi)
Melhor vácuo em laboratório
10-12
mmHg
psi

19. psi (pound force per square inch) ou libra por polegada
quadrada, é a unidade de pressão no sistema Inglaterra/americano:
1 psi x 0,068948 = 1 bar
1 bar x 14,50368 = 1 psi

20. Pressão manométrica

21. • Exemplo 1. Uma sala de estar tem 4,2 m de
comprimento, 3,5 m de largura e 2,4 m de
altura.
a) Qual é o peso do ar contido na sala se a
pressão do ar é 1,0 atm (densidade ar =
1,21 kg/m3)?
b) Qual é a força que a atmosfera exerce, de
cima para baixo, sobre a cabeça de uma
pessoa, que tem uma área de 0,040 m2?
Respostas: a) 418 N b) 4,00 x 103N

22. • Exemplo 2 (Exerc. 1 Halliday, vol 2 9ª ed)
Um peixe se mantém na mesma profundidade
na água doce ajustando a quantidade de ar em
ossos porosos ou bolsas de ar para tornar sua
massa específica média igual a da água.
Suponha que, com as bolsas de ar vazias, um
peixe tem uma massa específica de 1,08 g/cm3.
Para que fração de seu volume expandido o
peixe deve inflar as bolsas de ar para tornar
sua massa específica igual à da água?
• Resposta:0,074

23. • Exemplo 3. Uma janela de escritório tem
3,4 m de largura por 2,1 m de altura. Como
resultado da passagem de uma tempestade,
a pressão do ar do lado de fora do edifício
cai para 0,96 atm, mas no interior do
edifício permanece 1,0 atm. Qual o módulo
da força que empurra a janela para fora
por causa dessa diferença de pressão?
• Resposta: 2,9 x 104 N

24. Fluidos em
Repouso

25. • Pressão na profundidade h e na altitude d

26. Pressão 1 atm de coluna de água

27. • Pergunta

28. Medindo a pressão

29. d
l

30. Princípio de Pascal
Blaise Pascal (1623-1662)
“Uma variação de pressão aplicada em um
fluido incompressível contido em um
recipiente é inteiramente transmitida para
toda porção do fluido e para as paredes do
recipiente ”

31. • Uma aplicação importante desse princípio é
a prensa hidráulica, que consiste em dois
vasos comunicantes, com êmbolos de áreas
diferentes (A1 e A2 ) sobre as superfícies
livres do líquido contido nos vasos.

32. Prensa Hidráulica
• Aplicando-se uma força F1 sobre o êmbolo
de área A1 , a pressão exercida é propagada
pelo líquido até o êmbolo de área A2 .
• Força em 2
• Deslocamento em 2
• Trabalho em 2

33. Outra aplicação

34. Exemplo 5
Na prensa hidráulica na
figura ao lado, os
diâmetros dos tubos 1 e 2
são , respectivamente, 4
cm e 20 cm. Sendo o peso
do carro igual a 10 kN,
determine:
a) a força que deve ser
aplicada no tubo 1 para
equilibrar o carro;
b) o deslocamento do nível
de óleo no tubo 1, quando
o carro sobe 20 cm.
a) 400N b) 500cm

35. Princípio de Arquimedes

36. Princípio de Arquimedes
mg

37. Empuxo e equilíbrio
Nível da água
CG corpo
CG do empuxo

38. Princípio de Arquimedes
• “Quando um corpo está total ou
parcialmente submerso em um fluido uma
força de empuxo Fe exercida pelo fluido
age sobre o corpo. A força é dirigida para
cima e tem módulo igual ao peso do fluido
deslocado pelo corpo.”

39. Peso Aparente

40. Exemplo 6
• Considere o bloco da figura (quadro) com
massa específica igual a 800 kg/m3 que
flutua em um fluido de massa específica
1200 kg/m3. O bloco tem uma altura H=6,0
cm. a) Qual é a altura h da parte submersa
do bloco? b) Se o bloco for totalmente
submerso e depois liberado, qual será o
módulo da sua aceleração?

41. • Exemplo 7. Uma esfera de
alumínio maciço, de raio 9
cm, é suspensa por um fio e,
então, completamente imersa
em um recipiente cheio de
água ( = 998 kg/m3). A
densidade do alumínio é 2,7 x
103 kg/m3. Calcule a tensão
no fio (a) antes e (b) depois
da imersão do alumínio na
água. Respostas: a) 81 N, b)
50,9 N

42. Fluidos Ideais em Movimento
• Fluidos reais -> diversos parâmetros para
modelar
• Fluido ideal->matematicamente mais
fácil de analisar

43. Fluidos Ideais em Movimento
• Escoamento é laminar ou Escoamento é estacionário:
velocidade de um ponto do fluido não varia com o tempo
– Velocidade = cte
• Escoamento incompressível: massa específica tem valor
uniforme e constante.
– Líquidos apenas.
– Massa específica = cte
• Escoamento não-viscoso: análogo ao atrito nos sólidos
– Viscosidade = 0
• Escoamento irrotacional: não turbulento, não há vórtices

44. • Para observar o escoamento de um fluido
mtraçadores (corantes ou fumaça) ou
simulação (CFD)

45. Túnel de vento

46. Como o ar sustenta um avião?

47. A Equação da Continuidade
• Uma das primeiras leis da Hidrodinâmica foi obtida pelo
matemático e físico italiano Benedetto Castelli (15771644), em 1628, ao afirmar que:
• “Em uma corrente líquida estacionária em um
conduto, as velocidades são inversamente
proporcionais às secções transversais do
conduto.”
• Essa proposição é hoje conhecida como Equação da
Continuidade.

48. Equação da Continuidade
L
Definindo Fluxo
Fluxo de massa
Vazão mássica
A
V

49. Equação da Continuidade
conservação de massa
Vazão 1= Vazão 2
Vazão volumétrica

50. Exemplo 8
A0
h
A
•
•
•
•
•
A0=1,2 cm2
A=0,35 cm2
h=45 mm
g= 9,8 m/s2
34
RV=? cm3/s

51. Equação de Bernoulli

52. Equação de Bernoulli
•
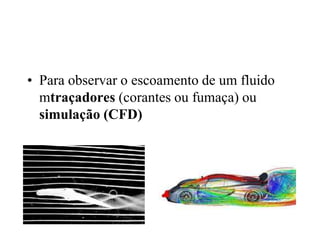
Para um fluido em escoamento
estacionário em uma tubulação, o teorema
do trabalho-energia cinética (W = K)
permite-nos escrever:
WG + WP = ( V/2)[v22
v12]
onde m = V é a massa de fluido em um
certo volume V, que entra no segmento de
tubulação considerado com velocidade de
módulo v1 e sai com velocidade de módulo
v2 e onde:
e
Lembrete:
F=pA
V=∆xA
WG =
Vg(y2
y1)
WP = F2 x2 + F1 x1 = (p2 p1)V
representam, respectivamente, o trabalho
da força gravitacional e o trabalho do resto
do fluido sobre a porção considerada.

53. Equação de Bernoulli
• Substituindo os W s na primeira equação e
reorganizando os termos vem:
p1 + gy1 + ( /2)v12 = p2 + gy2 + ( /2)v22
Esta é a equação de Bernoulli. Uma outra
forma de apresentá-la é a seguinte:
p + gy + ( /2)v2 = constante

54. Exemplo 9
Um grande tanque de armazenamento de
água, com a parte superior aberto, está
cheio até a altura h0 =12 m. O tanque é
perfurado a uma altura h = 8 m acima do
fundo. Qual é o alcance jato de água que
saí pelo furo?
R: 11,3 m

55. Exemplo 10
• A água entra em uma casa através de
um tubo que vem da rua da
fornecedora com diâmetro interno de
2,0 cm, com uma pressão absoluta de
igual a 4,0 x 10 5 Pa (cerca de 4 atm) e
velocidade de 1,5 m/s. Um tubo com
diâmetro interno de 1 cm conduz a
água para o banheiro no segundo andar
da casa a 5 m de altura. Calcule (a) a
velocidade de escoamento, (b) a
pressão e (c) a vazão volumétrica no
banheiro.
2
1

56. Aplicações das Equações de
Bernoulli e da Continuidade
• A equação de Bernoulli pode ser empregada
para determinar a velocidade de fluidos,
mediante a medida de pressões
– Medidor de Venturi
– Tubo de Pitot

57. Medidor de Venturi
C
A
B

58. Variação da Velocidade em um
Tubo com Vazão Constante

59. Medidor de Venturi
• Medir o escoamento de um fluido por meio de
medidas de pressões

60. Exemplo

61. Tubo de Pitot

62. Tubo de Pitot
• Medir velocidade de escoamento de um gás (ar, por exemplo)

66. Fórmula para o Pitot
ar
Massa
específica
manométrica

67. Como o ar sustenta um avião?
Em relação ao avião, o ar situado ao redor das asas se move para
trás. As asas apresentam uma certa curvatura na face inferior e
uma curvatura maior na face superior. Assim, as moléculas de ar
que passam por cima da asa o fazem com uma velocidade maior
do que aquelas que passam por baixo, porque devem percorrer
uma distância maior no mesmo intervalo de tempo. O caminho
percorrido por cada partícula do ar é chamado linha de corrente.
Na figura, aparecem duas linhas de corrente.

68. Como o ar sustenta um avião?
•
Para um fluido incompressível em regime estacionário, vale a
equação de Bernoulli, que expressa o princípio de
conservação da energia ao longo de cada linha de corrente:
p + gy + ½ v2 = constante
onde p representa a pressão, , a densidade e v, o módulo da
velocidade do fluido, g, o módulo da aceleração gravitacional e y, a
altura do ponto considerado no fluido em relação a um nivel de
referência arbitrário.

69. Como o ar sustenta um avião?
•
Aplicando a equação de Bernoulli aos pontos A e B temos:
pA + gyA + ½ vA2 = pB + gyB + ½ vB2
ou:
pA
pB = ½ [ vB2
vA2 ] + g[ yB
yA ]
Agora, como vB > vA e yB > yA, o lado direito da expressão
acima é positivo. Assim, pA > pB, ou seja, a pressão na parte
inferior da asa é maior do que a pressão na parte superior.
Isto significa que
existe uma força
resultante de baixo para
cima, responsável pela
sustentação do avião,
cujo módulo é dado por
F = A [ pA pB ], onde A
é a área da asa.

70. Referências
• Halliday & Resnick - Fundamentos de
Física, vol. 2, Cap. 14, 9ª edição, editora
LTC.
• Sears & Zemanski – Física I, Mecânica, 12ª
edição, Pearson, 2008.
• Material internet