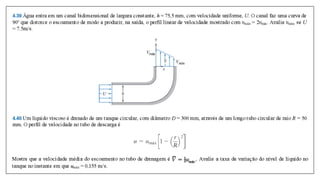
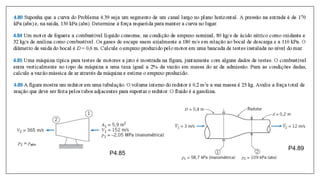
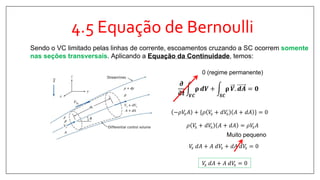
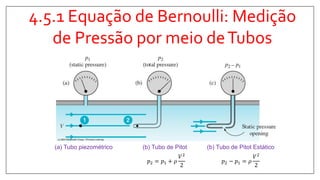
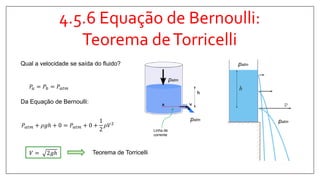
1) O documento discute os princípios básicos da mecânica dos fluidos, incluindo a conservação da massa, quantidade de movimento e energia.
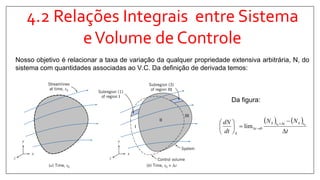
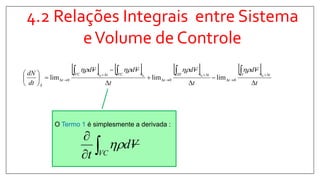
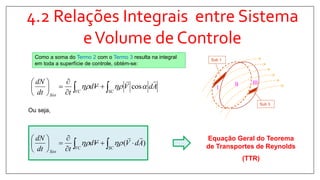
2) Apresenta o Teorema do Transporte de Reynolds (TTR), que relaciona a taxa de variação de propriedades em um sistema com fluxos através dos limites de um volume de controle.
3) Explica a aplicação do TTR para derivar equações de conservação para a massa, quantidade de movimento, energia e entropia.


















![4.2 Relações Integrais entre Sistema
eVolume de Controle
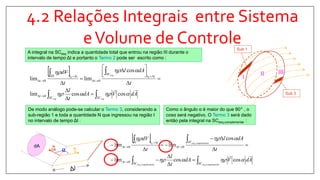
A quantidade dN3 contida na sub-região
3 é dada por :
tttt dAldN 00
)]cos([)3
Para a Região III inteira, tem-se então :
ttSCesq
dAl
0
cos
Observando uma vista ampliada da
sub-região 3 :
tttt VddN 00
][)3
𝑑𝑁3 𝑡0+∆𝑡
= 𝜂 𝜌 𝑉. 𝑑𝐴 ∆𝑡](https://image.slidesharecdn.com/mecnicadosfludosi-capitulo4-170307204556/85/Mecanica-dos-fluidos-i-capitulo-4-21-320.jpg)






















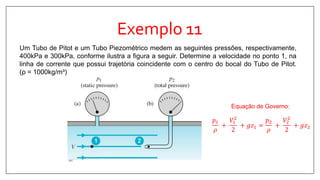






![Exemplo 14
Um volume de controle fixo é ilustrado na figura a seguir. Sabe-se que o escoamento se dá em
regime permanente e as propriedades relativas ao fluxos de massa em suas seções abertas
apresentam-se na tabela. Determine: as vazões volumétricas nas três seções; os fluxos de
massa nas três seções (faça um balanço do fluxo de massa do sistema); e a taxa de variação
da energia do sistema que ocupa o volume de controle.
Seção Tipo ρ [kg/m³] V [m/s] A [m²] e [J/kg]
1 Entrada 800 5 2 300
2 Entrada 800 8 3 100
3 Saída 800 17 2 150
𝒅𝑬
𝒅𝒕 𝒔𝒊𝒔𝒕𝒆𝒎𝒂
=
𝝏
𝝏𝒕
𝑽𝑪
𝒆𝝆𝒅∀ +
𝑺𝑪
𝒆𝝆(𝑽 ∙ 𝒅𝑨
Equação de
Governo:](https://image.slidesharecdn.com/mecnicadosfludosi-capitulo4-170307204556/85/Mecanica-dos-fluidos-i-capitulo-4-64-320.jpg)