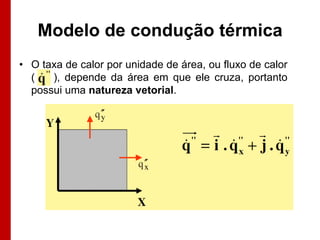
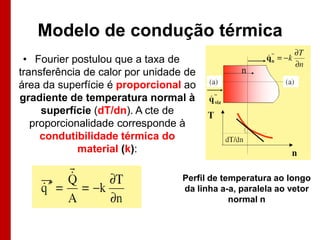
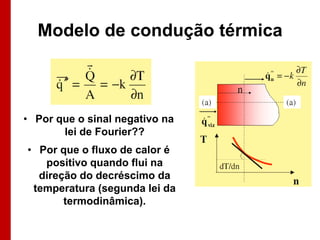
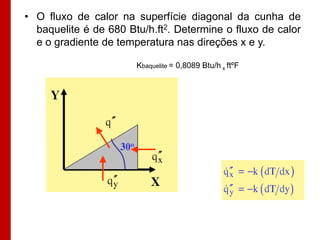
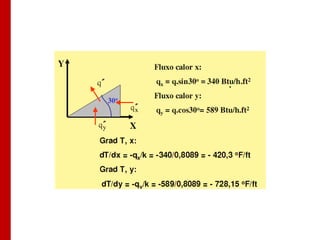
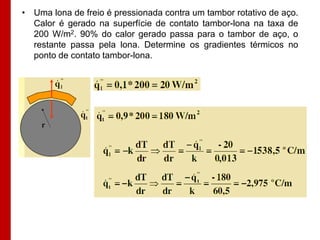
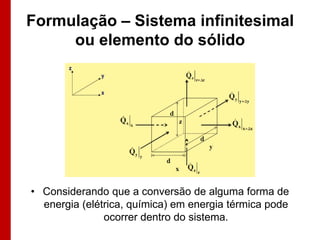
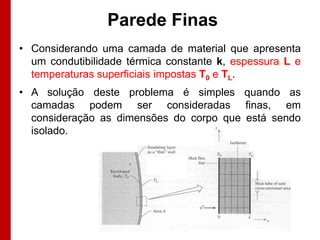
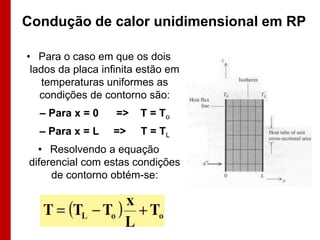
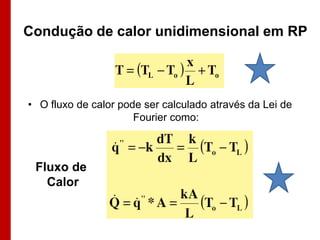
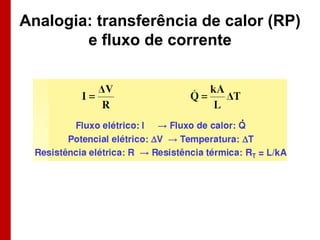
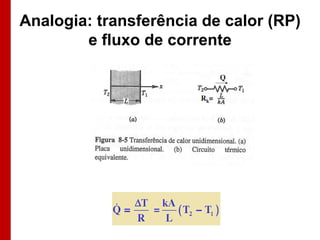
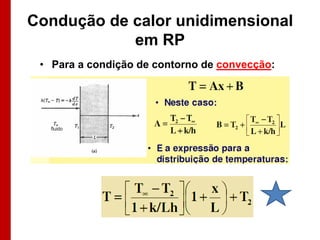
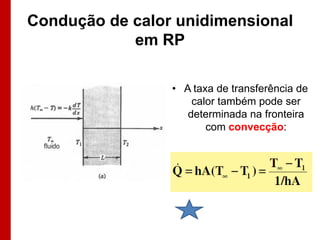
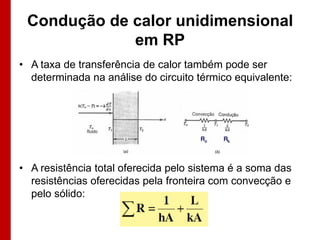
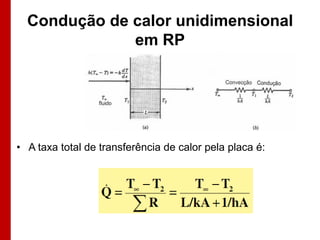
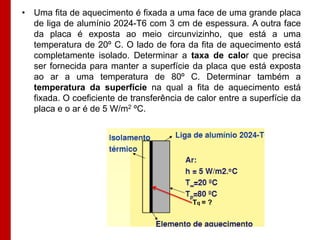
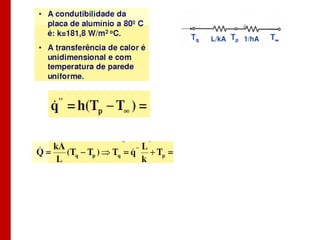
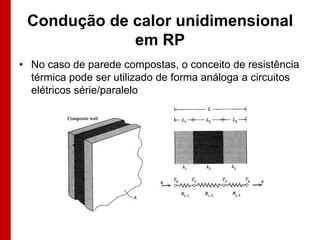
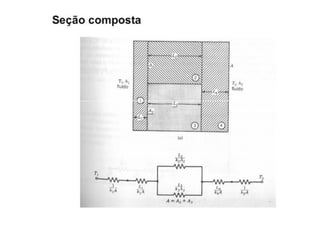
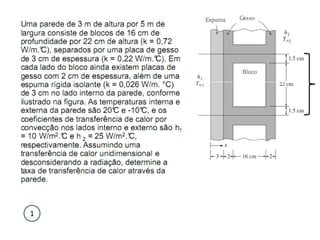
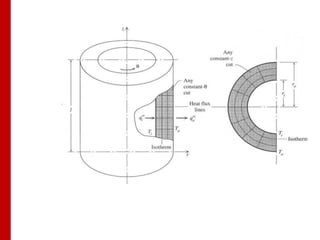
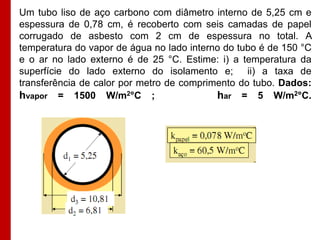
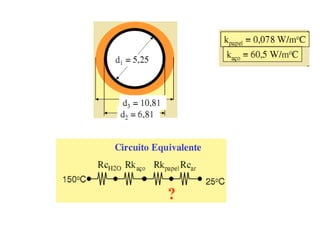
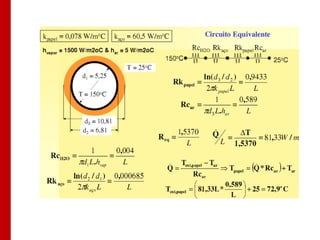
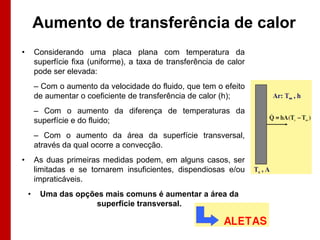
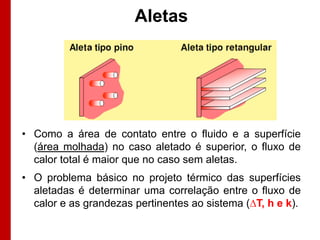
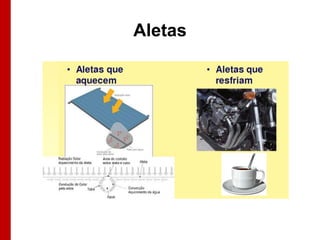
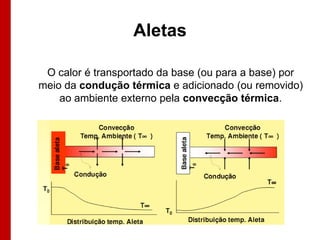
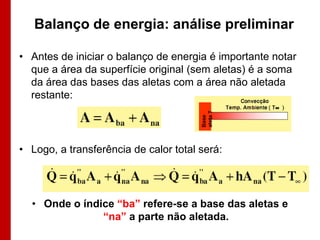
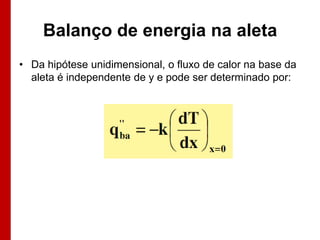
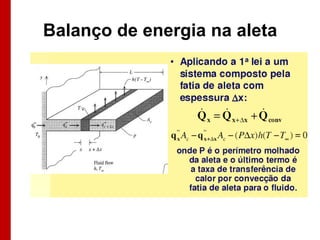
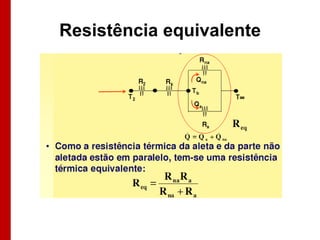
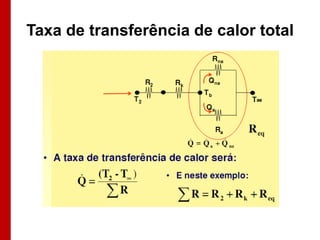
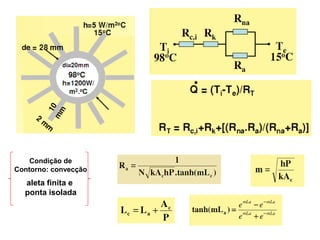
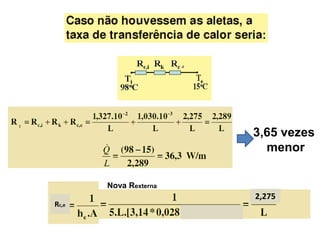
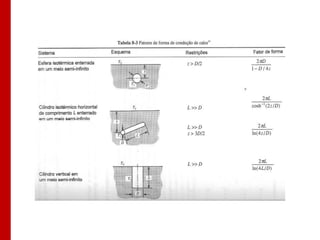
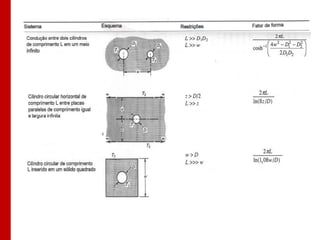
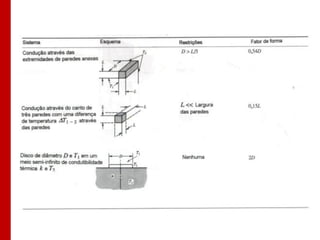
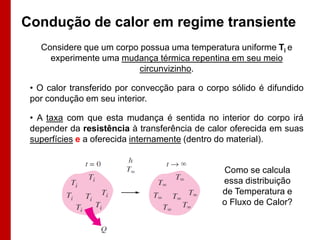
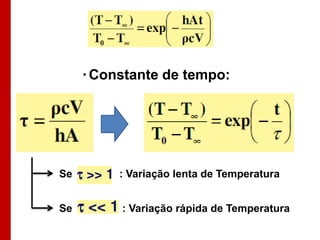
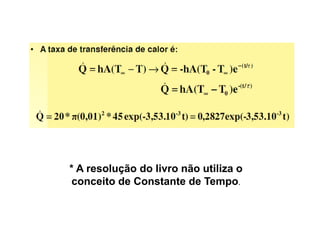
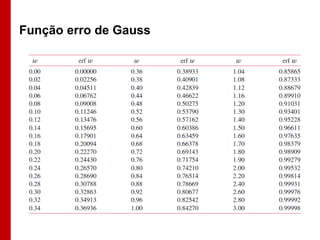
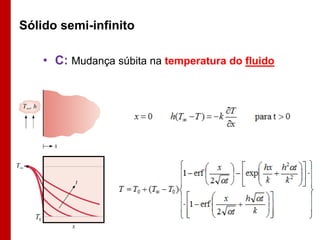
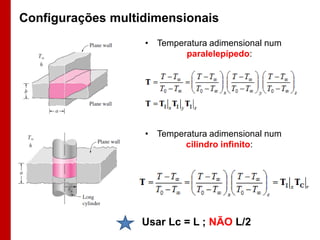
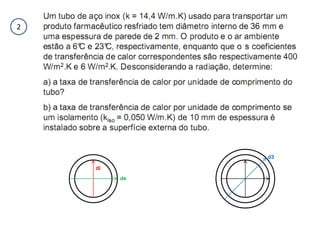
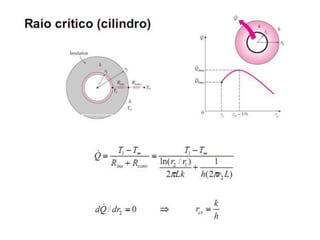
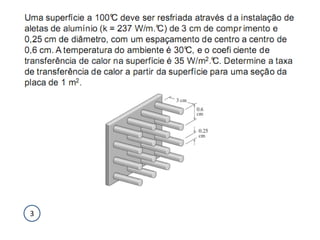
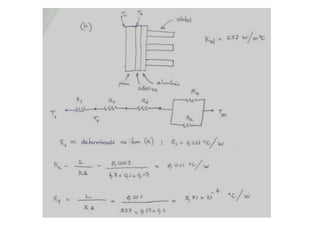
O documento discute os conceitos de transferência de calor por condução. Aborda a equação da condução de calor, casos de condução unidimensional em regime permanente e transiente, além de conceitos como condutibilidade térmica, condições de contorno e uso de aletas para aumentar a transferência de calor.