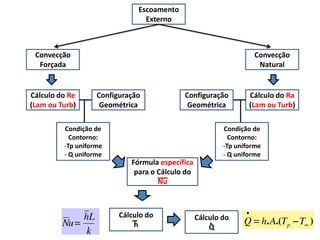
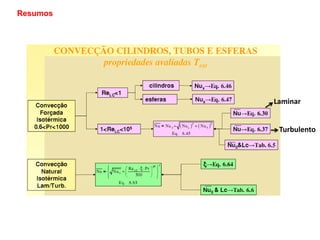
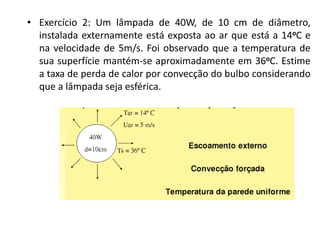
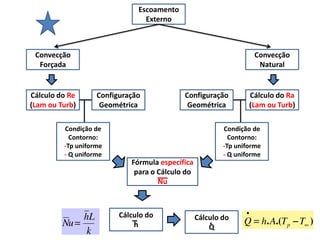
1. O documento discute conceitos fundamentais de escoamento externo, incluindo efeitos viscosos e térmicos, propriedades de fluidos, tipos de escoamento, camada limite, número de Reynolds, e arrasto viscoso.
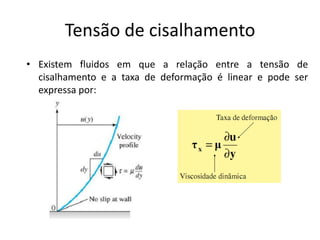
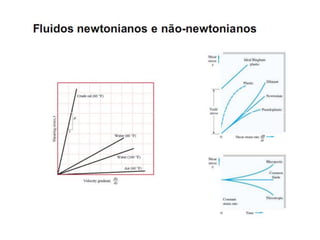
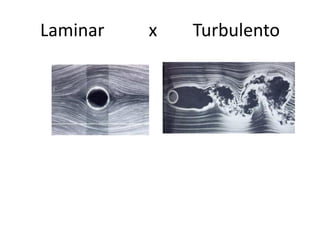
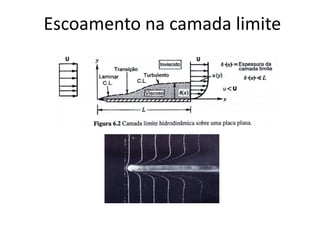
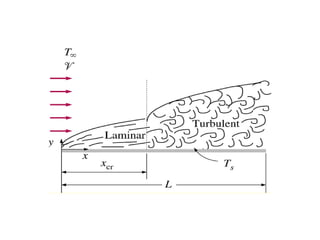
2. São apresentados os conceitos de escoamento laminar e turbulento, fluidos newtonianos e não-newtonianos, e escoamento em regime permanente e transiente.
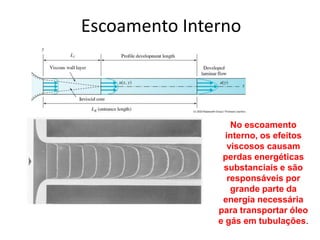
3. O resumo destaca os principais tipos de escoamento como incompressível e compressível, externo e interno, natural e






































































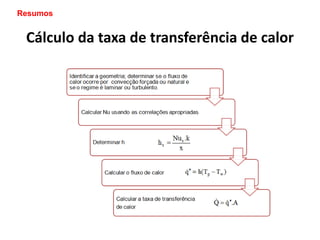
![Fluxo de Calor por Convecção
• Pode ser determinado por: Lei de resfriamento de Newton
Calor total transferido em [W]
Onde h = coeficiente de transferência de calor por convecção;
Tp= temperatura da superfície;
T∞ = temperatura do fluido fora da camada limite.
ou
Fluxo de calor por unidade
de área [W/m2]](https://image.slidesharecdn.com/captulo6-111005070154-phpapp01/85/Capitulo-6-98-320.jpg)