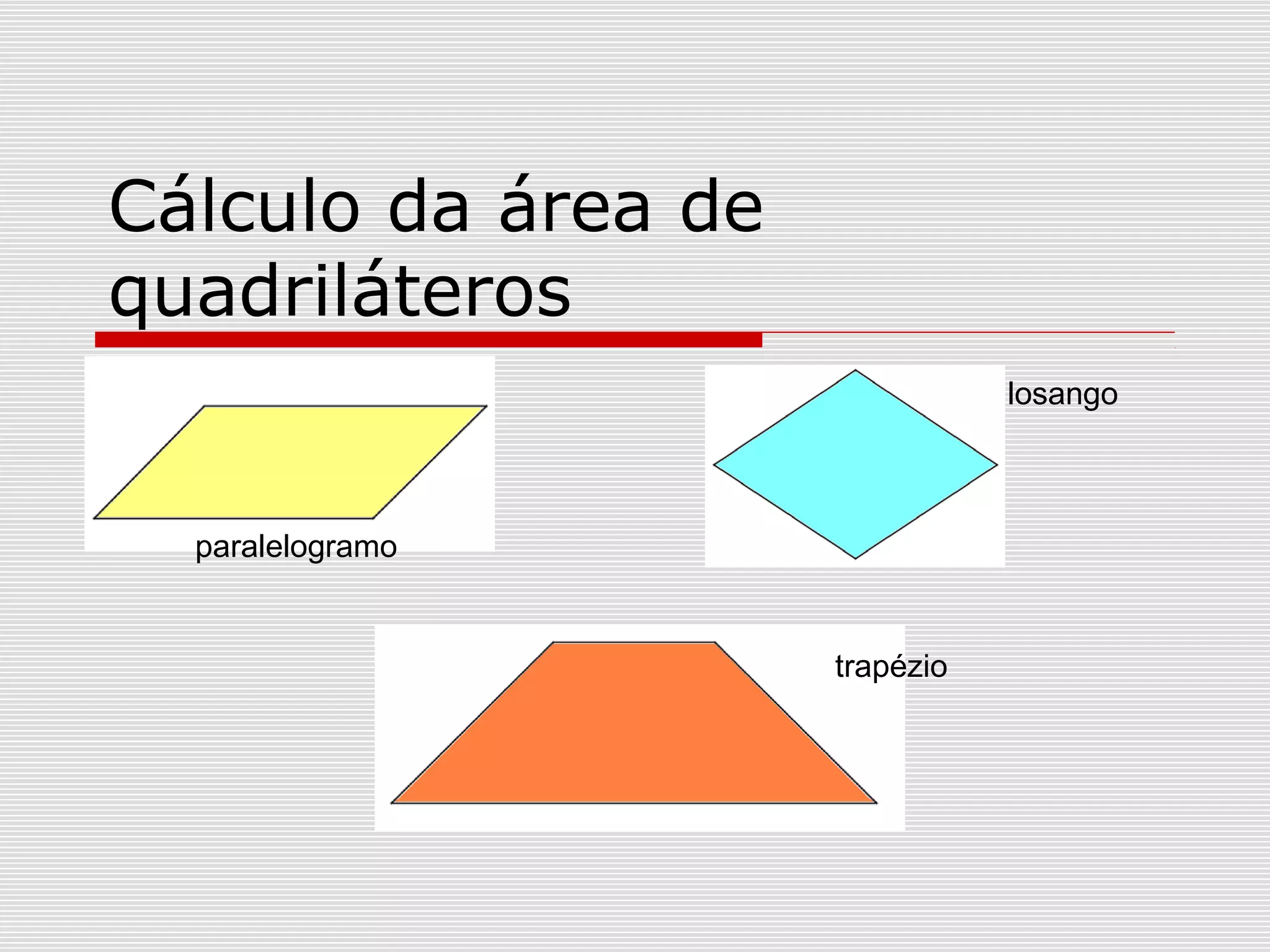
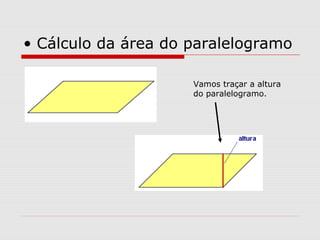
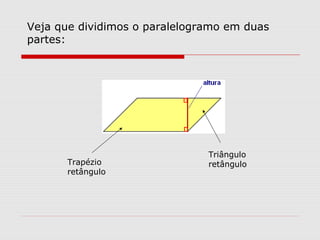
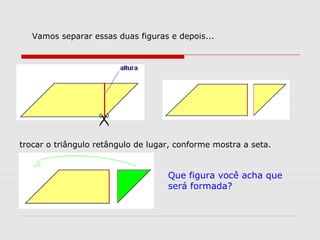
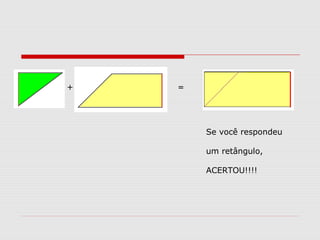
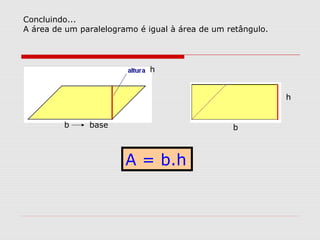
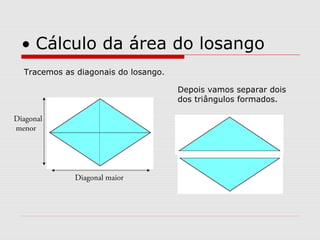
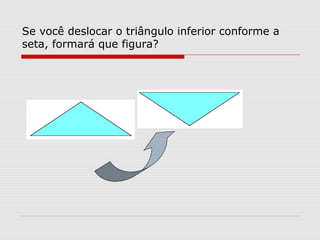
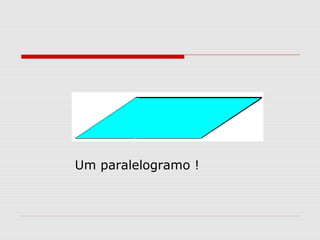
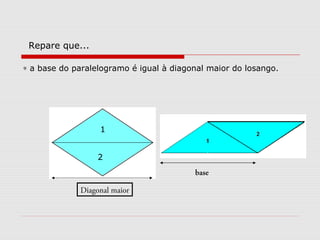
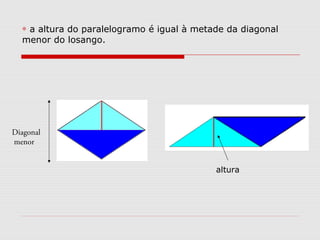
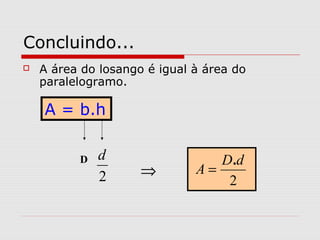
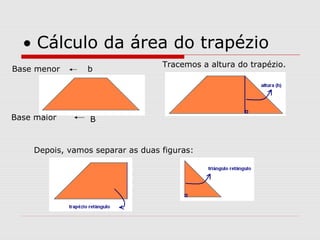
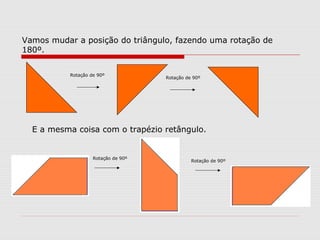
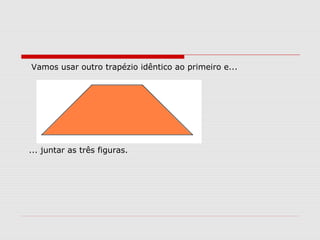
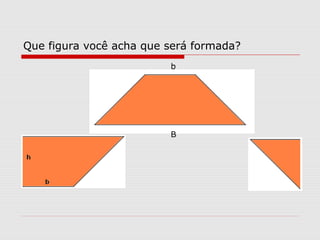
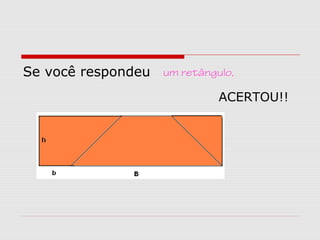
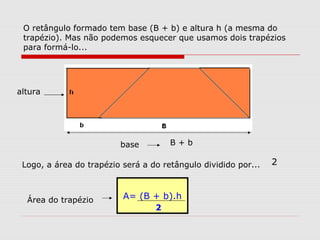
O documento explica como calcular a área de paralelogramos, losangos e trapézios. Para paralelogramos, a área é igual à de um retângulo com a mesma base e altura. Nos losangos, a área é igual à de um paralelogramo com base igual à diagonal maior e altura metade da diagonal menor. Já nos trapézios, ao juntar dois deles forma-se um retângulo cuja área divide-se por dois para obter a área do trapézio.

1. Cálculo da área de
quadriláteros
paralelogramo
losango
trapézio

2. • Cálculo da área do paralelogramo
Vamos traçar a altura
do paralelogramo.

3. Veja que dividimos o paralelogramo em duas
partes:
Trapézio
retângulo
Triângulo
retângulo

4. Vamos separar essas duas figuras e depois...

trocar o triângulo retângulo de lugar, conforme mostra a seta.
Que figura você acha que
será formada?

5. Se você respondeu
um retângulo,
ACERTOU!!!!
+ =

6. Concluindo...
A área de um paralelogramo é igual à área de um retângulo.
A = b.h
b base
h
b
h

7. • Cálculo da área do losango
Tracemos as diagonais do losango.
Depois vamos separar dois
dos triângulos formados.
Diagonal maior
Diagonal
menor

8. Se você deslocar o triângulo inferior conforme a
seta, formará que figura?

9. Um paralelogramo !

10. Repare que...
∗ a base do paralelogramo é igual à diagonal maior do losango.
Diagonal maior
1
2
base

11. ∗ a altura do paralelogramo é igual à metade da diagonal
menor do losango.
Diagonal
menor
altura

12. Concluindo...
 A área do losango é igual à área do
paralelogramo.
2
dD
A
.
=
A = b.h
⇒2
dD

13. • Cálculo da área do trapézio
Tracemos a altura do trapézio.
Depois, vamos separar as duas figuras:
b
B
Base menor
Base maior

14. Vamos mudar a posição do triângulo, fazendo uma rotação de
180º.
E a mesma coisa com o trapézio retângulo.
Rotação de 90º
Rotação de 90º
Rotação de 90º
Rotação de 90º

15. Vamos usar outro trapézio idêntico ao primeiro e...
... juntar as três figuras.

16. Que figura você acha que será formada?
b
B

17. Se você respondeu um retângulo,
ACERTOU!!

18. A= (B + b).h
O retângulo formado tem base (B + b) e altura h (a mesma do
trapézio). Mas não podemos esquecer que usamos dois trapézios
para formá-lo...
Logo, a área do trapézio será a do retângulo dividido por...
altura
base B + b
2
2
Área do trapézio