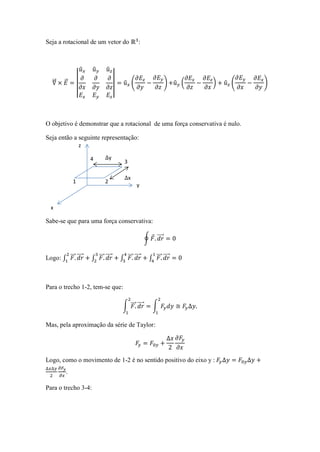
O documento demonstra que o rotacional de uma força conservativa é nulo. Ele faz isso calculando o rotacional ao longo de caminhos fechados em diferentes planos utilizando a aproximação de Taylor e a noção de sentidos dos eixos, mostrando que cada integral se anula.

1. Seja a rotacional de um vetor do :
̂ ̂ ̂
⃗ ⃗ |
| |
| ̂ ( ) ̂ ( ) ̂ ( )
O objetivo é demonstrar que a rotacional de uma força conservativa é nulo.
Seja então a seguinte representação:
z
4 y
3
x
1 2
y
x
Sabe-se que para uma força conservativa:
∮ ⃗⃗⃗⃗
Logo: ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗
Para o trecho 1-2, tem-se que:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫
Mas, pela aproximação da série de Taylor:
Logo, como o movimento de 1-2 é no sentido positivo do eixo y :
.
Para o trecho 3-4:

2. ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫
Mas, pela aproximação da série de Taylor, como a variação neste sentido é negativa,
temos:
Logo, como o deslocamento é no sentido contrário ao sentido do eixo y:
.
Analogamente para o trecho 2-3:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫
Pela aproximação da série de Taylor, como a variação em relação a x é negativa:
Logo, como o deslocamento ocorre no sentido contrário ao eixo x:
.
Para o trecho 4-1, analogamente:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ .
Logo:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗
( ) ⇒ ( )

3. A seguir serão mostrados rapidamente os resultados no planos xz e yz. Nestes
dois planos também será utilizada a aproximação por fórmula de Taylor e a noção dos
sentidos dos eixos.
Seja agora o seguinte caminho fechado:
3 z
2
z
4
y
1 x
x
Como a força é conservativa:
∮ ⃗⃗⃗⃗
Logo: ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗
Para o trecho 1-2, tem-se que:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫
Mas:
Logo, como o deslocamento é no sentido positivo do eixo: .
Para o trecho 3-4:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫

4. Mas:
Logo, como o deslocamento é no sentido contrário ao do eixo:
.
Analogamente para o trecho 2-3:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫
Logo: .
Para o trecho 4-1, analogamente:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ .
Logo:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗
( ) ⇒ ( ) ( )
Seja agora o seguinte caminho fechado:
4 y 3
z
z
1 2
y

5. x
Como a força é conservativa:
∮ ⃗⃗⃗⃗
Logo: ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗
Para o trecho 1-2, tem-se que:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫
Mas:
Logo, como o deslocamento é no sentido do eixo: .
Para o trecho 3-4:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫
Mas:
Logo, como o deslocamento é no sentido contrário ao eixo:
.
Analogamente para o trecho 2-3:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫

6. Logo: .
Para o trecho 4-1, analogamente:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ .
Logo:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗
( ) ⇒ ( ) ( )
Voltando ao rotacional:
̂ ̂ ̂
⃗ |
| |
| ̂ ( ) ̂ ( ) ̂ ( )
Mas, pelos cálculos efetuados anteriormente:
( ) ( ) ( )
Logo:
⃗
Conforme queria-se demonstrar.