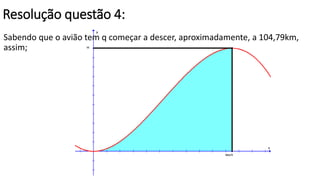
Este documento discute como calcular a trajetória de descida segura de uma aeronave se aproximando de um aeroporto. Ele encontra um polinômio cúbico que descreve a trajetória ideal, calcula a aceleração vertical máxima permitida e, com base nisso e nas condições iniciais, determina a distância ideal para iniciar a descida.

1. Trabalho de Cálculo
Onde um piloto deve iniciar a descida?
Higor Marioti
Luis Fernando
Mariana Martins

2. Problema: Um caminho de aproximação para uma
aeronave pousando é mostrado na
figura ao lado e satisfaz as seguintes
condições:
• (i) A altitude do voo é h, quando a
descida começa a uma distância
horizontal l do ponto de contato na
origem.
• (ii) O piloto deve manter uma
velocidade horizontal constante v em
toda a descida .
• (iii) O valor absoluto da aceleração
vertical não deve exceder uma
constante k( que é muito menos que a
aceleração da gravidade, 10m/s).

3. Questão 1:
Encontre um polinômio cúbico P(x) = ax³ + bx² + cx + d que satisfaça a
condição (i), impondo condições adequadas a P(x) e P'(x) no início da
descida e no ponto de contato.
Objetivo:
Encontrar um valor constantes para que a, b, c e d justificam a
trajetória de voo do avião.

4. Resolução questão 1:
P(0): a0³+b0²+c0+d = 0
d=0
Sabendo que o coeficiente angular do início (x=l) e final (x=0) é igual a
zero, pois a reta tangente formada pelo gráfico e paralela ao eixo x,
Assim:
P`(0): 3a0²+2b0+c=0
c=0

5. Substituindo os valores de c e d nas funções:
P(x) = ax³+bx²,
P'(x) = 3ax²+2bx.
Fazendo x=l nas equações acima:
P(l) = h
al³+bl²=h, (1)
P'(l) = 0
3al²+2bl=0.
Assim,
a = (-2b)/3l. (2)
Substituindo (2) em (1):
b=(3h)/l²;
Então, a = (-2h)/l³.
Assim, o polinômio P(x) que queríamos é igual:
P(x) = (-2h/l³)x³ + (3h/l²)x².

6. Resolução questão 2:
Uma vez que temos P(x) podemos fazer a derivada deste polinômio em
relação ao tempo t. Apesar de não haver esta variável no polinômio, entendemos
que a variável x é na verdade uma x(t). Então fazendo a derivada
de P(x) em t:
dP(x)/dt = (-2h/l³)3x²dx/dt + (3h/l²)2xdx/dt.
Mas sabemos que dx/dt é a variação da variável x no tempo, ou seja, é
na verdade a velocidade horizontal. E como foi estabelecido que durante a
descida o piloto deve manter a velocidade horizontal constante, temos que
dx/dt = v. Dessa forma, dP(x)/dt fica:
dP(x)/dt = (-2h/l³)3x²v + (3h/l²)2xv.

7. O polinômio P(x) determina a posição vertical y do avião em função da
sua posição horizontal x. Portanto, se y = P(x), a derivada segunda de
P(x(t)) em relação a t determina a aceleração vertical da aeronave. Sendo
assim, derivando dP(x)/dt em relação a t, lembrando que v é constante com
relação ao tempo, teremos:

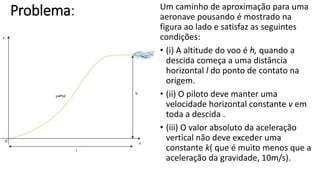
8. Como sabemos que o valor absoluto da componente vertical da aceleração
do avião não deve exceder uma constante k podemos fazer
Porem, x [0,l], segue que

9. Resolução questão 3:
Suponha que uma companhia aérea decida não permitir que a aceleração vertical
do avião exceda k = 1385 km/h². Se a altitude de cruzeiro do avião for 11km e a
velocidade for 480km/h, a que distância do aeroporto o piloto deveria começar a
descer?
Sabendo que:
6hv²/l² ≤ k
Então,
6*11*(480)²/l² ≤ 1385
66*230400/1385 ≤ l² (Obs: Nao alterei a desigualdade pois l² é um valor positivo)
10979,3501 ≤ l²
104,79km ≤ l

10. Resolução questão 4:
Sabendo que o avião tem q começar a descer, aproximadamente, a 104,79km,
assim;