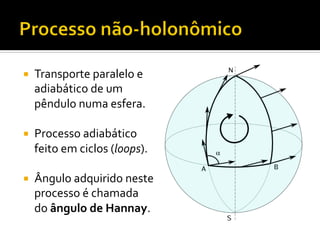
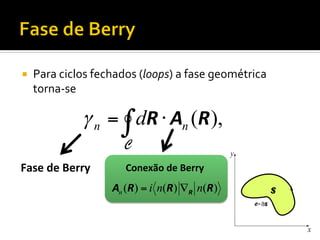
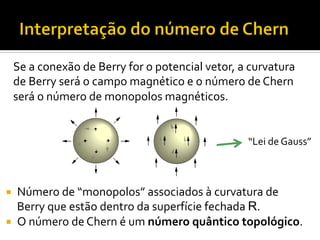
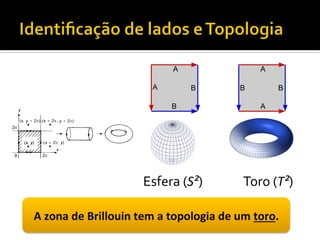
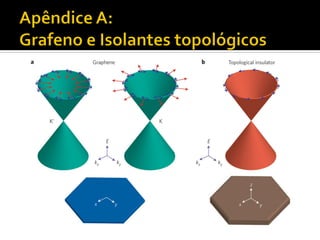
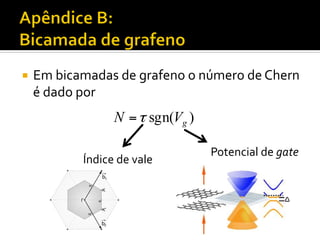
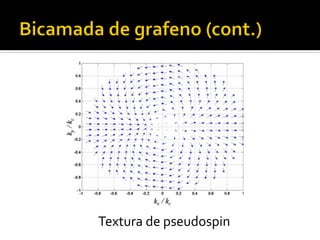
O documento discute transporte adiabático de um pêndulo em uma esfera e conceitos relacionados como evolução adiabática, fase geométrica, conexão de Berry, curvatura de Berry e número de Chern. Apresenta exemplos como o caso de um diabolo e sistemas periódicos descritos por uma zona de Brillouin em forma de toro.

1. Leandro
Seixas
SAMPA/IF/USP

2. ¡
Transporte
paralelo
e
adiabático
de
um
pêndulo
numa
esfera.
¡
Processo
adiabático
feito
em
ciclos
(loops).
¡
Ângulo
adquirido
neste
processo
é
chamada
do
ângulo
de
Hannay.

3. ¡ Em
uma
evolução
adiabática
o
sistema
varia
lentamente
com
o
tempo.
H(R) n(R) = ε n (R) n(R) ,
R = R(t )
Os
vetores
R(t)
pertencem
à
um
espaço
de
parâmetros
D-­‐dimensional
que
variam
adiabaticamente
no
tempo.
Teorema
adiabático
Um
sistema
com
autoestado
instantâneo
|n(R)
〉
que
evolui
adiabaticamente
permanece
no
mesmo
estado
ao
longo
da
evolução.

4. ¡ Quando
o
sistema
evolui
adiabaticamente
o
estado
quântico
dependente
do
tempo
é
ψ n (t ) = e
Fase
geométrica
Tem
origem
na
evolução
adiabá3ca
iγ n ( t ) iϑn ( t )
e
n(R)
Fase
dinâmica
Tem
origem
na
equação
de
Schrödinger
dependente
do
tempo
com
Hamiltoniano
H(t).
t
1
ϑn (t ) = − ∫ dt ' ε n (t ' )
!0

5. Substituindo
o
estado
na
equação
de
Schrödinger,
obtemos
i
d
⎡ "
⎤
ε n (R ) n(R ) = i! ⎢iγ n n(R ) − ε n (R ) n(R ) + n(R ) ⎥
!
dt
⎣
⎦
Fazendo
o
produto
interno
com
〈n(R)| e
usando
a
regra
da
cadeia
para
R=R(t),
chegamos
em
d
dR
γ n (t ) = i n(R ) ∇ R n(R )
dt
dt
Integrando
de
0
à
T,
obtemos
Rf
γ n (T ) = ∫ i n(R) ∇R n(R) ⋅ dR
Ri
γ n (0) = 0

6. ¡
Para
ciclos
fechados
(loops)
a
fase
geométrica
torna-­‐se
γ n = ∫ dR ⋅ An (R ),
C
Fase
de
Berry
Conexão
de
Berry
An (R) = i n(R) ∇R n(R)

7. ¡ Usando
o
teorema
de
Stokes,
a
fase
de
Berry
é
descrita
por
γ n (S) = ∫ dS ⋅ Ωn (R )
S
Curvatura
de
Berry
Teorema
de
Stokes
(3D)
∫ dR ⋅ F (r ) = ∫ dS ⋅ ∇ × F (r )
C
S
Ωn (R) = ∇ × An (R)

8. A
conexão
de
Berry
pode
ser
escrita
de
forma
alternativa
como
An = − Im n ∇R n
A
curvatura
de
Berry
será
escrita
então
como
Ωn = − Im ∇R n × ∇R n
Aplicando
o
gradiente
na
equação
de
autovalores
na
equação
acima,
a
curvatura
de
Berry
torna-­‐se
Ωn = − Im ∑
n '≠ n
n ∇ R H n' × n' ∇ R H n
(En ' − En )2

9. ¡
Para
uma
superfície
fechada
R
(compacta
e
sem
bordas)
,
uma
superfície
S
⊂R
tem
um
complemento
Sc
Para
um
loop
C
no
sentido
anti-­‐horário
γ n (S) = ∫ dR ⋅ An (R ) = ∫ d S ⋅ Ωn (R )
C
S
Enquanto
que
no
sentido
horário
(loop
-­‐C)
a
fase
é
γ n (Sc ) = ∫ dR ⋅ An (R) = ∫ d S ⋅ Ωn (R)
−C
Sc

10. Uma
evolução
adiabática
em
um
loop
C
cria
uma
fase
que
é
a
inversa
do
loop
-­‐C (sentido
contrário)
e
iγ n (S )
=e
− iγ n (S c )
Usando
a
propriedade
da
superfície
fechada
R,
chegamos
em
γ n (S) + γ n (Sc ) = ∫ dS ⋅ Ωn (R) = 2πN
S∪Sc
¡
O
número
de
Chern
é
definido
por
1
N=
∫ dS ⋅ Ωn (R)
2π R
S∪ Sc = R
Lembrar:
Superfície
fechada!

11. Se
a
conexão
de
Berry
for
o
potencial
vetor,
a
curvatura
de
Berry
será
o
campo
magnético
e
o
número
de
Chern
será
o
número
de
monopolos
magnéticos.
“Lei
de
Gauss”
¡
¡
Número
de
“monopolos”
associados
à
curvatura
de
Berry
que
estão
dentro
da
superfície
fechada
R.
O
número
de
Chern
é
um
número
quântico
topológico.

12. ¡
Próximo
à
singularidades
H = h( R ) ⋅ σ
Os
auto-­‐estados
são
⎛ eiϕ sin (θ )⎞
2
⎟
u− (θ , ϕ ) = ⎜
⎜ − cos(θ ) ⎟
2 ⎠
⎝
Diabolo
⎛ eiϕ cos(θ )⎞
2
⎟
u+ (θ , ϕ ) = ⎜
⎜ sin (θ ) ⎟
2
⎝
⎠
A
conexão
de
Berry
e
a
curvatura
de
Berry
são
para
o
estado
de
mais
baixa
energia
são
A = − cos
ϕ
−
( ),
2 θ
2
A =0
θ
−
Ω−
θϕ
1
= sin θ
2

13. ¡
Para
o
caso
h = R = (x, y, z )
x − iy ⎞
⎛ z
O
Hamiltoniano
torna-­‐se
H = ⎜
⎜ x + iy − z ⎟
⎟
⎝
⎠
∂
u± (θ , ϕ )
∂x
∂
y
A± = i u± (θ , ϕ )
u± (θ , ϕ )
∂y
∂
z
A± = i u± (θ , ϕ )
u± (θ , ϕ )
∂z
x
A± = i u± (θ , ϕ )
1 R
Ω± = ∓
2 R3
Componentes
da
conexão
de
Berry
“Campo
de
monopolo”

14. Sistemas
periódicos
que
são
descritos
por
uma
rede
Bravais
com
uma
base.
As
funções
de
onda
em
sólidos
são
descrita
pelo
teorema
de
Bloch.
Os
vetores
de
onda
k
estão
mapeados
dentro
da
zona
de
Brillouin.
Teorema
de
Bloch
ψ n (r + a) = e
ik ⋅a
ψ n (r )
ψ n (r ) = eik⋅x un k (r )

15. Esfera
(S²)
Toro
(T²)
A
zona
de
Brillouin
tem
a
topologia
de
um
toro.

16. Em
uma
teoria
semiclássica,
a
perturbação
do
campo
elétrico
E
muda
adiabaticamente
os
vetores
de
onda
k
" = −eE ⇒ k(t) = − e Et
!k
!
Devido
à
topologia
da
zona
de
Brillouin,
a
perturbação
do
campo
elétrico
faz
um
loop
no
espaço
de
parâmetros.
A
evolução
adiabática
em
sólidos
fornece
γ n ( k ) = ∫ d 2 k ⋅ Ωn ( k )
BZ
Ωn (k ) = ∇k × unk (r ) i∇k unk (r )

17. ¡ A
fase
de
Berry
é
usada
para:
1.
2.
3.
4.
Efeito
Aharonov-­‐Bohm
Teoria
moderna
de
polarização
em
materiais
ferroelétricos
Teoria
moderna
de
magnetização
em
materiais
ferromagnéticos
Teoria
de
efeito
Hall
quântico
(Teoria
TKNN)
Efeito
Hall
inteiro
2. Efeito
Hall
anômalo
(Grafeno
e
bicamada
de
grafeno)
3. Efeito
Hall
de
spin
(Isolantes
topológicos)
1.

18. •
•
•
•
•
Xiao
D.,
Chang,
M.
&
Niu
Q.
Rev.
Mod.
Phys.
82,
1959
(2010).
Griffiths,
D.
J.
Introduction
to
Quantum
Mechanics.
Benjamin
Cummings,
2º
edição.
Berry,
M.
V.
Proc.
R.
Soc.
Lond.
A
392,
45
(1984).
Zak,
J.
Phys.
Rev.
Lett.
62,
2747
(1989).
Garg,
A.
Am.
J.
Phys.
78,
661
(2010)

20. ¡ Em
bicamadas
de
grafeno
o
número
de
Chern
é
dado
por
N = τ sgn(Vg )
Índice
de
vale
Potencial
de
gate

21. Textura
de
pseudospin

22. ¡
Para
um
espaço
de
parâmetros
de
dimensão
D,
temos:
n
γ n (S) = ∫ 1 dR µ ∧ dRν Ωµν ( R) = ∫ Ω n
2
S
S
n
γ n = ∫ dR µ Aµ (R)
C
n
onde
Ω
é
conhecido
como
2-­‐forma
de
curvatura
(funcional
de
um
tensor
de
rank
2).
Aplicação
de
geometria
diferencial
para
o
espaço
de
parâmetros
(espaço
curvo)
de
D
dimensões.

23. ¡
Fazendo
a
transformação
de
calibre
na
conexão
de
Berry
An (R) → An (R) − ∇Rζ (R)
Podemos
ver
que
a
curvatura
de
Berry
é
invariante
de
calibre
Ωn (R ) → Ωn (R )
E
a
fase
de
Berry
pode
mudar
no
máximo
por
um
múltiplo
inteiro
de
2π
γ n (S) → γ n (S) + 2πm