O documento descreve a análise do movimento de um foguete impulsionado por gases emitidos a uma taxa constante. Ele calcula expressões para a velocidade do foguete em função do tempo usando a segunda lei de Newton e integra essas expressões para obter a posição em função do tempo. Gráficos da velocidade e posição em função do tempo são plotados considerando valores numéricos específicos.

1. Considerando que em relação a um referencial inercial o foguete tenha uma
velocidade ⃗ ̂ para um dado tempo . Agora para um determinado tempo
temos que o gás tinha uma velocidade ⃗ ̂ , que a massa desse gás é
dada por e que a velocidade do foguete passou a ser ⃗ ( ) ̂ . Temos tal
situação na figura abaixo:
Determinemos o valor da expressão a seguir:
⃗⃗ ⃗⃗ ( ) ⃗⃗ ( ) ( )⃗ ( )⃗ ⃗
Agora, a partir do valor acima, calculemos a seguinte expressão:
⃗⃗ ⃗
⃗ ⃗
Tomando o limite da função a cima para , tem-se que:
⃗
⃗ ⃗⃗

2. Onde ⃗⃗ ⃗ ⃗ representa a velocidade do gás em relação ao foguete.
Assim, como no caso analisado, a força externa é somente a força gravitacional,
temos, de acordo com a expressão obtida, que:
⃗
( ̂ ) (̂ ) ( ̂ )
Considerando que a taxa de emissão de gases é constante e igual a , ou seja,
⁄ , conseguimos obter a seguinte equação:
∫ ∫
Por outro lado, da expressão anterior a acima, tem-se que:
∫ ∫ ∫
Integrando a expressão acima respeitando os respectivos limites de integração,
tem-se que:
( ) ( )
Considerando que .
( )

3. Tomando:
=500Kg/s
Temos o seguinte gráfico da velocidade em função do tempo:
100000
80000
Velocidade (m/s)
60000
40000
20000
0
0 5 10 15 20
Tempo (s)
GRAFICO 1-VELOCIDADE
Note que essa função é válida para
Continuando, sabe-se que neste caso, , e com a expressão a pouco obtida,
tem-se que:
( ) ∫ ∫ ∫ ∫ ( )
Fazendo , tem-se que:
∫
Tem-se por fim que:

4. [( ) ( ) ]
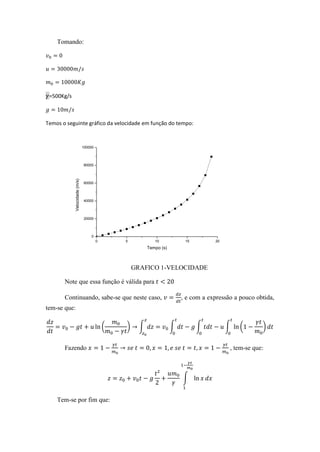
Tomando:
=500Kg/s
Temos o seguinte gráfico da posição em função do tempo:
1000000
800000
Posiçao(m)
600000
400000
200000
0
0 2 4 6 8 10 12 14 16 18 20
Tempo(s)
GRAFICO 2-POSIÇÃO
Note que essa função é válida para
OBS: Gráficos plotados no Origin PRO versão 8.