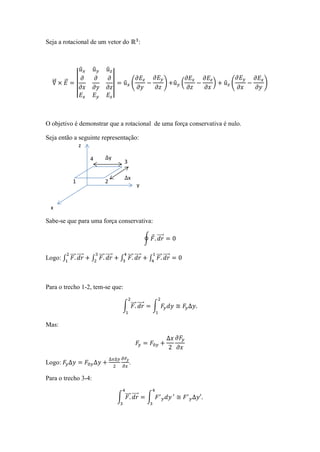
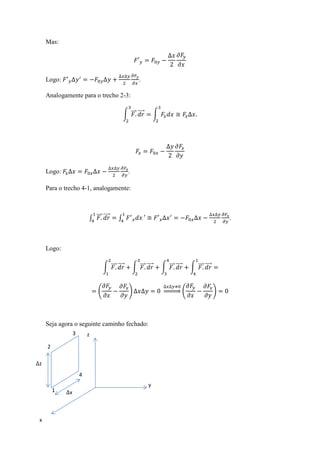
O documento demonstra que o rotacional de uma força conservativa é nulo através de cálculos de integrais de linha. Ele calcula as integrais de linha ao redor de dois caminhos fechados diferentes para mostrar que o resultado é sempre zero, indicando que o rotacional é nulo para forças conservativas.

1. Seja a rotacional de um vetor do :
̂ ̂ ̂
⃗ ⃗ |
| |
| ̂ ( ) ̂ ( ) ̂ ( )
O objetivo é demonstrar que a rotacional de uma força conservativa é nulo.
Seja então a seguinte representação:
z
4 y
3
x
1 2
y
x
Sabe-se que para uma força conservativa:
∮ ⃗⃗⃗⃗
Logo: ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗
Para o trecho 1-2, tem-se que:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫
Mas:
Logo: .
Para o trecho 3-4:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫

2. Mas:
Logo: .
Analogamente para o trecho 2-3:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫
Logo: .
Para o trecho 4-1, analogamente:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ .
Logo:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗
( ) ⇒ ( )
Seja agora o seguinte caminho fechado:
3 z
2
z
4
y
1 x
x

3. Como a força é conservativa:
∮ ⃗⃗⃗⃗
Logo: ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗
Para o trecho 1-2, tem-se que:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫
Mas:
Logo: .
Para o trecho 3-4:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫
Mas:
Logo: .
Analogamente para o trecho 2-3:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫
Logo: .
Para o trecho 4-1, analogamente:

4. ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ .
Logo:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗
( ) ⇒ ( ) ( )
Seja agora o seguinte caminho fechado:
4 y 3
z
z
1 2
y
x
Como a força é conservativa:
∮ ⃗⃗⃗⃗
Logo: ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗
Para o trecho 1-2, tem-se que:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫
Mas:

5. Logo: .
Para o trecho 3-4:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫
Mas:
Logo: .
Analogamente para o trecho 2-3:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫
Logo: .
Para o trecho 4-1, analogamente:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ .
Logo:
∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗ ∫ ⃗⃗⃗ ⃗⃗⃗⃗
( ) ⇒ ( ) ( )
Voltando ao rotacional:
̂ ̂ ̂
⃗ |
| |
| ̂ ( ) ̂ ( ) ̂ ( )

6. Mas, pelos cálculos efetuados anteriormente:
( ) ( ) ( )
Logo:
⃗
Conforme queria-se demonstrar.