O documento descreve o método dos esforços para resolver estruturas hiperestáticas. O método envolve substituir vínculos por carregamentos externos para criar uma estrutura equivalente isostática. As deformações da estrutura original e equivalente são igualadas através de equações de compatibilidade para determinar os esforços internos.

1. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 1 / 37
MÉTODO DOS ESFORÇOS
Na resolução de estruturas hiperestáticas (aquelas que não podem ser resolvidas com as 3
equações fundamentais da estática , a saber : somatória forças verticais igual a zero , somatória
forças horizontais igual a zero , somatória momento fletor referente a um ponto igual a zero) , nós
podemos lançar mão do método dos esforços. Este processo de cálculo consiste na utilização de
uma estrutura equivalente a que desejamos calcular, na qual substituímos um vínculo entre barras
ou entre barra e apoio por um carregamento externo. Vejamos alguns exemplos de modificação
abaixo :
A estrutura equivalente deve ser isostática, caso a estrutura continue hiperestática após a
primeira modificação, executamos outra modificação e assim por diante até encontrar uma estrutura
equivalente isostática. A estrutura equivalente deve ser desdobrada em:
ISOSTÁTICA BÁSICA – corresponde a estrutura equivalente com os carregamentos externos da viga original .
CASO (1) – corresponde a estrutura equivalente com o carregamento originado pela primeira modificação.
CASO (2) – corresponde a estrutura equivalente com o carregamento originado pela segunda modificação.
CASO (n) – corresponde a estrutura equivalente com o carregamento originado pela enésima modificação.
Vale um comentário quanto a numeração da estrutura: deve-se procurar numerar os nós da
estrutura de forma que o ponto 1 coincida com a modificação 1 , o ponto 2 com a modificação 2 e
assim por diante, e, caso seja possível, desaconselha-se duas modificações no mesmo nó.
≡
X
≡
X
≡
X
≡
XX
≡
XX
≡
X
X

2. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 2 / 37
Para conseguirmos determinar as incógnitas que superam o número de equações
fundamentais da Estática vamos usar equações de compatibilidade de deformação (seja esta
deformação a flecha, o giro, ou o giro relativo). Ou seja , valendo a sobreposição de efeitos :
- na modificação do apoio móvel do nó “1” por uma força “X”, temos que a soma da flecha
devida ao carregamento externo original com a flecha devida a força “X” será igual a zero
(condição de apoio na estrutura original).
δ1R = δ10 + δ11 → 0 = δ10 + δ11
- na modificação do engastamento do nó “1” por um momento fletor “X” e um apoio fixo, temos
que a soma do giro devido ao carregamento externo original com o giro devido ao momento
“X” será igual a zero (condição de engastamento na estrutura original).
ϕ1R = ϕ10 + ϕ11 → 0 = ϕ10 + ϕ11
- na modificação da ligação rígida entre barras no nó “1” por uma articulação com momentos
fletores relativos “X”, diremos que a soma do giro relativo devido ao carregamento externo
original com o giro relativo devido aos momentos fletores relativos “X” será igual a zero
(condição de ligação rígida - continuidade - na estrutura original).
ϕR1R = ϕR10 + ϕR11 → 0 = ϕR10 + ϕR11
Os cálculos relativos a flecha, giro e giro relativo serão desenvolvidos com o Teorema de
Castigliano e auxílio da Tabela de Kurt Beyer. Para tanto devemos construir os diagramas de
momento fletor da Isostática Básica e dos “n” Casos. Uma vez que o Teorema de Castigliano utiliza
de um diagrama de momento gerado por um carregamento unitário, convém em cada Caso (“n”)
colocarmos em evidência Xn tornando assim cada Caso (“n”) em um carregamento unitário
multiplicado por Xn.
Cria-se a equação de compatibilidade na seguinte forma :
REAL = CASO (0) + X1 . CASO (1) + X2 . CASO (2) + ... + Xn . CASO (n)
Castigliano : dx
IE
MMo
⋅
⋅
⋅
= ∫
1
δ , dx
IE
MMo
⋅
⋅
⋅
= ∫ 1
ϕ , dx
IE
MMo
R ⋅
⋅
⋅
= ∫
1
ϕ
Encontradas as deformações por Castigliano , montamos um sistema linear devido as
equações de compatibilidade com a seguinte forma :

3. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 3 / 37
⎪
⎪
⎩
⎪
⎪
⎨
⎧
++++=
++++=
++++=
nnnnnnnR
nnR
nnR
XXX
XXX
XXX
ϕϕϕϕϕ
ϕϕϕϕϕ
ϕϕϕϕϕ
......
.....................
......
......
22110
2222211202
1122111101
⎪
⎪
⎩
⎪
⎪
⎨
⎧
++++=
++++=
++++=
nnnnnn
nn
nn
XXX
XXX
XXX
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
......0
.....................
......0
......0
22110
222221120
112211110
Os valores encontrados nos fornecem os vínculos ou esforços internos aos quais se referem,
tornando possível agora a resolução da estrutura original utilizando-se as 3 equações fundamentais
da estática, seguindo o cálculo das reações de apoio e a construção dos diagramas de esforços
internos solicitantes da estrutura original, a saber N (esforço normal) , V (esforço cortante) e M
(momento fletor) .
EXERCÍCIO 01 : Na viga contínua esquematizada abaixo , calcular os diagramas de
esforços internos solicitantes :
Resolução :
Definição da viga equivalente e numeração da estrutura (Caso Real) :
20 kN
/m
4,0 m
1,5 m 2,0 m
3,0 m
30 kN40 kN
E , I → constantes
20 kN
/m
4,0 m
1,5 m 2,0 m
3,0 m
30 kN40 kN
X X
0 1 2
ϕR1R = 0

4. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 4 / 37
Desmembramento da estrutura em Caso (0) – Isostática Básica e Caso (1) , com seus respectivos
gráficos de momento fletor :
Cálculo dos giros relativos ϕR10 , ϕR11 por Castigliano :
∫= dx
IE
MM
R .
.
. 10
10ϕ
( ) ( )⎟
⎠
⎞
⎜
⎝
⎛
+++++== ∫ βαϕ 1.
6
..
1.
6
..
3
..
3
..
.
.
1
...
.
1
1010
kiskiskiskis
IE
dxMM
IE
R
20 kN
/m
4,0 m
1,5 m 2,0 m
3,0 m
30 kN40 kN
0 1 2
ϕR10
CASO (0)
M0 kN.m
40,0
22,5
+
M0
kN.m
30,0 30,0
4,0 m3,0 m
0 1 2
1,0
M1 kN.m
1,0
X . CASO (1)
1,0
ϕR11

5. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 5 / 37
( ) ( )
IEIE
R
..3
385
5,01.
6
1.30.4
5,01.
6
1.30.3
3
1.40.4
3
1.5,22.3
.
.
1
10 +=⎟
⎠
⎞
⎜
⎝
⎛
+++++=ϕ
∫= dx
IE
MM
R .
.
. 11
11ϕ
IEIE
kiskis
IE
dxMM
IE
R
..3
7
3
1.1.4
3
1.1.3
.
.
1
3
..
3
..
.
.
1
...
.
1
1110 +=⎟
⎠
⎞
⎜
⎝
⎛
+=⎟
⎠
⎞
⎜
⎝
⎛
+== ∫ϕ
Montagem sistema linear com equação de compatibilidade :
( R ) = ( 0 ) + X . ( 1 ) ⇒ ϕR1R = ϕR10 + X . ϕR11
IE
X
IE ..3
7
.
..3
385
0 ++= ⇒ 00,55
7
..3
.
..3
385
−=−=
IE
IE
X
∴ podemos assim afirmar que o momento fletor no apoio (1) assume o valor X . 1,0 kN.m , ou seja,
vale –55,00 kN.m . O sinal negativo indica que ele assume sentido contrário ao escolhido na
proposição do caso (1) .
Cálculo das Reações de Apoio e Diagrama de Esforços Internos Solicitantes
∑ −= 00,551esqM ⇒ 5,1.3.205,1.403.55 0 −−+=− VR ⇒ 0 31,67VR kN= +
∑ −= 00,551dirM ⇒ 2.4.202.304.55 2 −−+=− VR ⇒ 2 41,25VR kN= +
∑ = 0VF ⇒ 020.73040210 =−−−+++ VVV RRR ⇒ 1 137,08VR kN= +
∑ = 0HF ⇒ 02 =HR

6. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 6 / 37
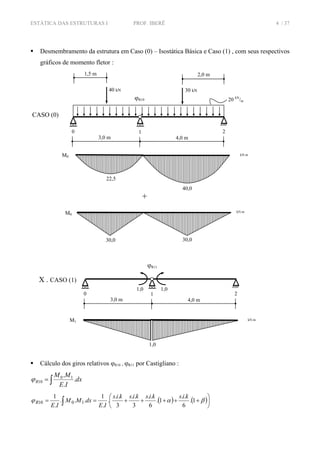
EXERCÍCIO 02 : Na viga contínua esquematizada abaixo , calcular os diagramas de
esforços internos solicitantes :
20 kN
/m
4,0 m
1,5 m 2,0 m
3,0 m
30 kN40 kN
0 1 2
RV 0 RV 1 RV 2
RH 2
+
–
+
–
N 0 [kN]
V
+
+
–
–
31,67
1,67
38,33
68,33
68,75
28,75
1,25
41,25
[kN]
+
–
M
25,00
55,00
42,50
[kN.m]
40 kN
/m
3,0 m
2,0 m
3,0 m
30 kN
E → constante
1,0 m
20 kN
/m
I 3.I 3.I

7. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 7 / 37
Resolução :
Definição da viga equivalente e numeração da estrutura (Caso Real) :
Desmembramento da estrutura em Caso (0) – Isostática Básica e Caso (1) , com seus respectivos
gráficos de momento fletor :
X X0 1 2
ϕR1R = 0 40 kN
/m
3,0 m
2,0 m
3,0 m
30 kN
20 kN
/m
I 3.I
20 kN.m
40 kN
M0 kN.m
45,0
22,5
+
CASO (0)
0 1 2
ϕR10 40 kN
/m
3,0 m
2,0 m
3,0 m
30 kN
20 kN
/m
I 3.I
20 kN.m
40 kN
M0
kN.m
20,0
20,0

8. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 8 / 37
Cálculo dos giros relativos ϕR10 , ϕR11 por Castigliano :
∫∫∫∫∫ +=+==
2
1
10
1
0
10
2
1
10
1
0
1010
10 ...
..3
1
...
.
1
.
..3
.
.
.
.
.
.
.
dxMM
IE
dxMM
IE
dx
IE
MM
dx
IE
MM
dx
IE
MM
Rϕ
( ) ⎟
⎠
⎞
⎜
⎝
⎛
−+⎟
⎠
⎞
⎜
⎝
⎛
++=
6
..
3
..
.
..3
1
1.
6
..
3
..
.
.
1
10
kiskis
IE
kiskis
IE
R αϕ
IEIEIE
R
..6
305
6
20.1.3
3
1.45.3
.
..3
1
3
2
1.
6
20.1.3
3
1.5,22.3
.
.
1
10 +=⎟
⎠
⎞
⎜
⎝
⎛
−+⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
++=ϕ
∫∫∫∫∫ +=+==
2
1
11
1
0
11
2
1
11
1
0
1111
11 ...
..3
1
...
.
1
.
..3
.
.
.
.
.
.
.
dxMM
IE
dxMM
IE
dx
IE
MM
dx
IE
MM
dx
IE
MM
Rϕ
IEIEIE
kis
IE
kis
IE
R
..3
4
3
1.1.3
.
..3
1
3
1.1.3
.
.
1
3
..
.
..3
1
3
..
.
.
1
10 +=⎟
⎠
⎞
⎜
⎝
⎛
+⎟
⎠
⎞
⎜
⎝
⎛
=⎟
⎠
⎞
⎜
⎝
⎛
+⎟
⎠
⎞
⎜
⎝
⎛
=ϕ
Montagem sistema linear com equação de compatibilidade :
( R ) = ( 0 ) + X . ( 1 ) ⇒ ϕR1R = ϕR10 + X . ϕR11
IE
X
IE ..3
4
.
..6
305
0 ++= ⇒ 12,38
4
..3
.
..6
305
−=−=
IE
IE
X
∴ podemos assim afirmar que o momento fletor no apoio (1) assume o valor X . 1,0 kN.m , ou seja,
vale –38,12 kN.m . O sinal negativo indica que ele assume sentido contrário ao escolhido na
proposição do caso (1) .
Cálculo das Reações de Apoio e Diagrama de Esforços Internos Solicitantes
3,0 m3,0 m
0 1 2
1,0
M1 kN.m
1,0
X . CASO (1)
1,0
ϕR11

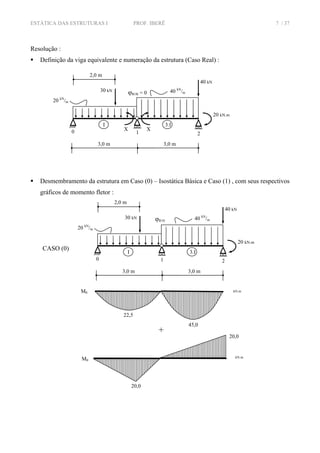
9. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 9 / 37
∑ −= 12,381esqM ⇒ 5,1.3.201.303.12,38 0 −−+=− VR ⇒ 0 27,29VR kN= +
∑ −= 12,381dirM ⇒ 2.4.403.12,38 2 −+=− VR ⇒ 2 93,96VR kN= +
∑ = 0VF ⇒ 040.420.330210 =−−−+++ VVV RRR ⇒ 1 128,75VR kN= +
∑ = 0HF ⇒ 00 =HR
3,0 m
0 1 2
RV 0 RV 1 RV 2
RH 0
+
–
+
–
N 0 [kN]
V
++
–
–
27,29
42,71
12,71
62,71
66,04
40,00
53,96
[kN]
+
–
M
18,62
38,12
16,42
[kN.m]
40 kN
/m
3,0 m
2,0 m
30 kN
1,0 m
20 kN
/m
I 3.I 3.I
+
1,365 1,35
20,00

10. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 10 / 37
EXERCÍCIO 03 : Na viga contínua esquematizada abaixo , calcular os diagramas de
esforços internos solicitantes :
Resolução :
Definição da viga equivalente e numeração da estrutura (Caso Real) :
Desmembramento da estrutura em Caso (0) – Isostática Básica e Caso (1) , com seus respectivos
gráficos de momento fletor :
18 kN
/m
4,0 m 3,0 m
E , I → constantes
3,0 m 1,0 m
24 kN
/m
18 kN
/m
4,0 m 3,0 m3,0 m
24 kN
/m
18 kN
9 kN.m
X1 X2X2 X3X3
1 2 3 4
ϕ1R = 0
ϕR2R = 0 ϕR3R = 0
M0 kN.m
20,25
48,00
+
M0
kN.m
9,00
CASO (0)
18 kN
/m
4,0 m 3,0 m3,0 m
24 kN
/m
18 kN
9 kN.m
1 2 3 4
ϕ10
ϕR20 ϕR30
20,25

11. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 11 / 37
Cálculo dos giros relativos ϕR20 , ϕR30 , ϕR21 , ϕR22 , ϕR23 , ϕR31 , ϕR32 , ϕR33 , e dos giros ϕ10 , ϕ11 , ϕ12 ,
ϕ13, por Castigliano :
IEIE
kis
IE
dxMM
IE
dx
IE
MM
.
64
3
1.48.4
.
.
1
3
..
.
.
1
...
.
1
.
.
.
10
10
10 +=⎟
⎠
⎞
⎜
⎝
⎛
=⎟
⎠
⎞
⎜
⎝
⎛
=== ∫∫ϕ
IEIE
kis
IE
dxMM
IE
dx
IE
MM
..3
4
3
1.1.4
.
.
1
3
..
.
.
1
...
.
1
.
.
.
11
11
11 +=⎟
⎠
⎞
⎜
⎝
⎛
=⎟
⎠
⎞
⎜
⎝
⎛
=== ∫∫ϕ
M1 kN.m
1,00
X1 . CASO (1)
4,0 m 3,0 m3,0 m
1,00
1 2 3 4
ϕ11 ϕR21 ϕR31
M2 kN.m
1,00
X2 . CASO (2)
4,0 m 3,0 m3,0 m
1,00
1 2 3 4
ϕ12 ϕR22 ϕR32
1,00
M3 kN.m
1,00
X3 . CASO (3)
4,0 m 3,0 m3,0 m
1,00
1 2 3 4
ϕ13 ϕR23 ϕR33
1,00

12. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 12 / 37
IEIE
kis
IE
dxMM
IE
dx
IE
MM
R
..3
2
6
1.1.4
.
.
1
6
..
.
.
1
...
.
1
.
.
.
21
21
2112 +=⎟
⎠
⎞
⎜
⎝
⎛
=⎟
⎠
⎞
⎜
⎝
⎛
==== ∫∫ϕϕ
00.
.
1
...
.
1
.
.
.
31
31
3113 ===== ∫∫ IE
dxMM
IE
dx
IE
MM
Rϕϕ
⎟
⎠
⎞
⎜
⎝
⎛
+=⎟
⎠
⎞
⎜
⎝
⎛
+=== ∫∫ 3
1.25,20.3
3
1.48.4
.
.
1
3
..
3
..
.
.
1
...
.
1
.
.
.
20
20
20
IE
kiskis
IE
dxMM
IE
dx
IE
MM
Rϕ
IE
R
..4
337
20 +=ϕ
IEIE
kiskis
IE
dxMM
IE
dx
IE
MM
R
..3
7
3
1.1.3
3
1.1.4
.
.
1
3
..
3
..
.
.
1
...
.
1
.
.
.
22
22
22 +=⎟
⎠
⎞
⎜
⎝
⎛
+=⎟
⎠
⎞
⎜
⎝
⎛
+=== ∫∫ϕ
IEIE
kis
IE
dxMM
IE
dx
IE
MM
RR
..2
1
6
1.1.3
.
.
1
6
..
.
.
1
...
.
1
.
.
.
32
32
3223 +=⎟
⎠
⎞
⎜
⎝
⎛
=⎟
⎠
⎞
⎜
⎝
⎛
==== ∫∫ϕϕ
⎟
⎠
⎞
⎜
⎝
⎛
−+=== ∫∫ 6
..
3
..
3
..
.
.
1
...
.
1
.
.
.
30
30
30
kiskiskis
IE
dxMM
IE
dx
IE
MM
Rϕ
IEIE
R
.
36
6
1.9.3
3
1.25,20.3
3
1.25,20.3
.
.
1
30 =⎟
⎠
⎞
⎜
⎝
⎛
−+=ϕ
IEIE
kiskis
IE
dxMM
IE
dx
IE
MM
R
.
2
3
1.1.3
3
1.1.3
.
.
1
3
..
3
..
.
.
1
...
.
1
.
.
.
33
33
33 +=⎟
⎠
⎞
⎜
⎝
⎛
+=⎟
⎠
⎞
⎜
⎝
⎛
+=== ∫∫ϕ
Montagem sistema linear com equação de compatibilidade :
( R ) = ( 0 ) + X1 . ( 1 ) + X2 . ( 2 ) + X3 . ( 3 ) ⇒
⎪
⎩
⎪
⎨
⎧
+++=
+++=
+++=
33332231130
23322221120
13312211110
...0
...0
...0
RRRR
RRRR
XXX
XXX
XXX
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
resolvendo o sistema por forma matricial :
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
30
20
10
3
2
1
333231
232221
131211
R
R
RRR
RRR
X
X
X
ϕ
ϕ
ϕ
ϕϕϕ
ϕϕϕ
ϕϕϕ
⇒
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
00,36
25,84
00,64
00,250,00
50,033,267,0
067,033,1
3
2
1
X
X
X
∴
23,12
07,23
47,36
3
2
1
−=
−=
−=
X
X
X
∴ podemos assim afirmar que : o momento reativo no engaste (1) assume o valor X1 . 1,0 kN.m ,
ou seja, vale –36,47 kN.m ; o momento fletor no apoio (2) assume o valor X2 . 1,0 kN.m , ou seja,

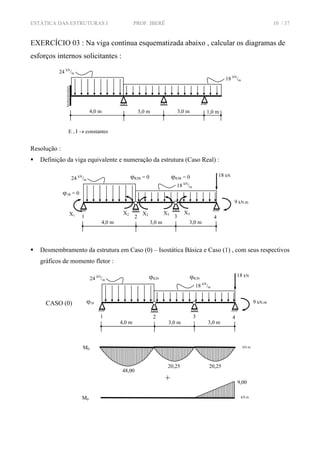
13. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 13 / 37
vale –23,07 kN.m ; o momento fletor no apoio (3) assume o valor X3 . 1,0 kN.m , ou seja, vale –12,23
kN.m . O sinal negativo indica que os momentos assumem sentido contrário ao escolhido na
proposição dos casos .
Cálculo das Reações de Apoio e Diagrama de Esforços Internos Solicitantes
∑ −= 07,232esqM ⇒ 2.4.244.47,3607,23 1 −+−=− VR ⇒ 1 51,35VR kN= +
∑ −= 23,123esqM ⇒ 5,1.3.183.2.4.247.35,5147,3623,12 2 −+−+−=− VR ⇒ 2 75,26VR kN= +
∑ −= 23,123dirM ⇒ 3.2.4.1823,12 4VR+−=− ⇒ 4 43,92VR kN= +
∑ −= 07,232dirM ⇒ 3.6.92,435,3.7.1807,23 3VR++−=− ⇒ 3 51,47VR kN= +
∑ = 0HF ⇒ 01 =HR ; 04 =HR
RV 1
RV 3RV 2
RH 4
+
–
+
–
N 0 [kN]
V
++
– –
51,35
44,65
2,14 m 23,39
30,61
18,0028,08
25,92
[kN]
+
–
M
18,48
36,47
23,07
[kN.m]
18 kN
/m
4,0 m 3,0 m3,0 m 1,0 m
24 kN
/m
RV 4
RH 1
–
+ +
1,70 m 1,56 m
2,95
12,23
9,67
9,00

14. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 14 / 37
EXERCÍCIO 04 : Na viga hiperestática esquematizada abaixo , calcular os diagramas
de esforços internos solicitantes :
Resolução :
a) utilizando a flecha do apoio (1) para montagem da equação de compatibilidade :
Definição da viga equivalente e numeração da estrutura (Caso Real) :
Desmembramento da estrutura em Caso (0) – Isostática Básica e Caso (1) , com seus respectivos
gráficos de momento fletor :
Cálculo das flechas δ10 , δ11 por Castigliano :
IEIE
kis
IE
dxMM
IE
dx
IE
MM
.
640
4
4.160.4
.
.
1
4
..
.
.
1
...
.
1
.
.
.
10
10
10 −=⎟
⎠
⎞
⎜
⎝
⎛
−=⎟
⎠
⎞
⎜
⎝
⎛
−=== ∫∫δ
4,0 m
E , I → constantes
20 kN
/m
4,0 m
X
20 kN
/m
0 1
δ1R = 0
M0
kN.mCASO (0)
4,0 m
20 kN
/m
0 1
δ10
M1
kN.mX . CASO (1)
4,0 m
0 1
δ11
1,0 kN
4
160

15. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 15 / 37
IEIE
kis
IE
dxMM
IE
dx
IE
MM
..3
64
3
4.4.4
.
.
1
3
..
.
.
1
...
.
1
.
.
.
11
11
11 =⎟
⎠
⎞
⎜
⎝
⎛
=⎟
⎠
⎞
⎜
⎝
⎛
=== ∫∫δ
Montagem sistema linear com equação de compatibilidade :
( R ) = ( 0 ) + X . ( 1 ) ⇒ δ1R = δ10 + X . δ11
IE
X
IE ..3
64
.
.
640
0 +−= ⇒ 00,30
64
..3
.
.
640
=+=
IE
IE
X
∴ podemos assim afirmar que a reação vertical no apoio (1) assume o valor X . 1,0 kN , ou seja,
vale 30,00 kN . O sinal positivo indica que ela assume o mesmo sentido escolhido na proposição do
caso (1).
Cálculo das Reações de Apoio
∑ = 00M ⇒ 02.4.204.300 =+−− RM ⇒ 0 40,00RM kN= +
∑ = 0VF ⇒ 020.4300 =−++ VR ⇒ 0 50,00VR kN= +
∑ = 0HF ⇒ 00 =HR
b) utilizando o giro do engaste (1) para montagem da equação de compatibilidade :
Definição da viga equivalente e numeração da estrutura (Caso Real) :
Desmembramento da estrutura em Caso (0) – Isostática Básica e Caso (1) , com seus respectivos
gráficos de momento fletor :
4,0
X
20 kN
/m
21
ϕ1R = 0
M0
kN.mCASO
4,0
20 kN
/m
21
ϕ10
M1
kN.mX . CASO (1)
4,0
21
ϕ11
1,0 kN.m
1
40

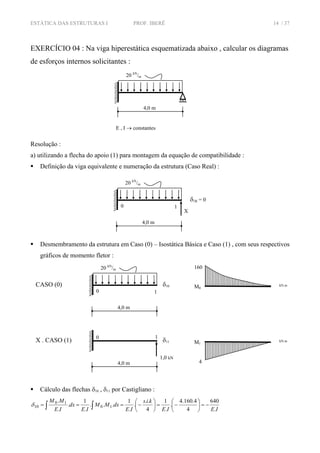
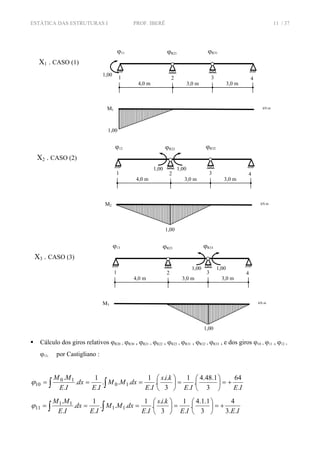
16. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 16 / 37
Cálculo dos giros ϕ10 , ϕ11 por Castigliano :
IEIE
kis
IE
dxMM
IE
dx
IE
MM
..3
160
3
1.40.4
.
.
1
3
..
.
.
1
...
.
1
.
.
.
10
10
10 −=⎟
⎠
⎞
⎜
⎝
⎛
−=⎟
⎠
⎞
⎜
⎝
⎛
−=== ∫∫ϕ
IEIE
kis
IE
dxMM
IE
dx
IE
MM
..3
4
3
1.1.4
.
.
1
3
..
.
.
1
...
.
1
.
.
.
11
11
11 =⎟
⎠
⎞
⎜
⎝
⎛
=⎟
⎠
⎞
⎜
⎝
⎛
=== ∫∫ϕ
Montagem sistema linear com equação de compatibilidade :
( R ) = ( 0 ) + X . ( 1 ) ⇒ ϕ1R = ϕ10 + X . ϕ11
IE
X
IE ..3
4
.
..3
160
0 +−= ⇒ 00,40
4
..3
.
..3
160
=+=
IE
IE
X
∴ podemos assim afirmar que o momento reativo no engaste (1) assume o valor X . 1,0 kN.m , ou
seja, vale 40,00 kN.m . O sinal positivo indica que ela assume o mesmo sentido escolhido na
proposição do caso (1) .
Cálculo das Reações de Apoio
∑ = 00M ⇒ 02.4.204.40 1 =+−− VR ⇒ 1 30,00VR kN= +
∑ = 0VF ⇒ 020.4300 =−++ VR ⇒ 0 50,00VR kN= +
∑ = 0HF ⇒ 00 =HR
RV 0 RV 1
RH 0
+
–
+
–
N 0 [kN]
V
+
–
50,0
30,0
[kN]
+
–
M
22,50
40,00
2,50 m
4,0
0
20 kN
/m
MR0
Diagramas de Esforços Internos Solicitantes
Nota : O exercício foi resolvido de duas
maneiras possíveis para demonstrar o método ,
no caso poderia ser utilizada a resolução a) ou
b) , que resultaram iguais como podemos
comprovar no item de cálculo das reações.

17. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 17 / 37
EXERCÍCIO 05 : Na estrutura esquematizada abaixo , calcular as reações de apoio e
os diagramas de esforços internos solicitantes :
Resolução :
Definição da estrutura equivalente e numeração (Caso Real) :
32 kN
/m
6,0 m
E , I → constantes
3,0m2,0m
24 kN
X1
ϕ1R = 0
32 kN
/m
6,0 m
E , I → constantes
3,0m2,0m
24 kN
2
1
3 4

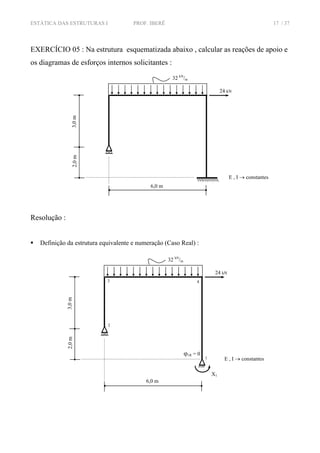
18. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 18 / 37
Desmembramento da estrutura em Caso (0) – Isostática Básica e Caso (1) , com seus respectivos
gráficos de momento fletor :
CASO (0)
ϕ10
32 kN
/m
6,0 m
3,0m2,0m
24 kN
2
1
3 4
24 kN
116 kN
76 kN
116
06.3276
0
76
03.6.325.246.
0
24
024
0
1
1
2
2
1
1
1
=
=−+
=
=
=−++
=
=
=−+
=
∑
∑
∑
V
V
V
V
V
H
H
H
R
R
F
R
R
M
R
R
F
M0 [ kN.m ]
144,00
2
3
0
3 4
120,00
3 4
4
1
120,00

19. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 19 / 37
Cálculo dos giros ϕ10 , ϕ11 , por Castigliano :
⎟
⎠
⎞
⎜
⎝
⎛
−−=== ∫∫ 2
..
3
..
3
..
.
.
1
...
.
1
.
.
.
10
10
10
kiskiskis
IE
dxMM
IE
dx
IE
MM
ϕ
IEIE .
252
2
120.1.5
3
120.1.6
3
144.1.6
.
.
1
10 −=⎟
⎠
⎞
⎜
⎝
⎛
−−=ϕ
⎟
⎠
⎞
⎜
⎝
⎛
+=== ∫∫ kis
kis
IE
dxMM
IE
dx
IE
MM
..
3
..
.
.
1
...
.
1
.
.
.
11
11
11ϕ
IEIE .
7
1.1.5
3
1.1.6
.
.
1
11 +=⎟
⎠
⎞
⎜
⎝
⎛
+=ϕ
X1 . CASO (1)
1,00
ϕ11
6,0 m
3,0m2,0m
2
1
3 4
0
1
/6 kN
6
1
1
6
1
1
6
1
2
2
1
1
0
0
016.
0
0
0
=
=+−
=
=
=−+
=
=
=
∑
∑
∑
V
V
V
V
V
H
H
R
R
F
R
R
M
R
F
1
/6 kN
M1 [ kN.m ]
2
3
0
3 4
1,00
4
11,00
1,00

20. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 20 / 37
Montagem sistema linear com equação de compatibilidade :
( R ) = ( 0 ) + X1 . ( 1 ) ⇒ 11110 .0 ϕϕ X+= ⇒
11
10
1
ϕ
ϕ
−=X
00,36
7
.
.
252
1 =⋅⎟
⎠
⎞
⎜
⎝
⎛
−−=
IE
IE
X
∴ podemos assim afirmar que o momento reativo no engaste (1) assume o valor X1 . 1,0 kN.m ,
ou seja, vale 36,00 kN.m . O sinal positivo indica que o momento assume o mesmo sentido ao
escolhido na proposição dos casos .
Cálculo das Reações de Apoio e Diagrama de Esforços Internos Solicitantes
( )1
61 116,00 36,00. 110,00VR kN= + − =
( )1 24,00 36,00. 0 24,00HR kN= + =
( )1
62 76,00 36,00. 82,00VR kN= + + =
82,00
82,00
–
–
110,00
110,00
0
N [ kN ]
82,00
–
110,00
24,00
0
V [ kN ]
+
+
24,00
2,56 m

21. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 21 / 37
EXERCÍCIO 06 : Na estrutura esquematizada abaixo , calcular as reações de apoio e
os diagramas de esforços internos solicitantes :
Resolução :
Definição da estrutura equivalente e numeração (Caso Real) :
84,00
84,00
105,06
36,00
0
M [ kN.m ]
2,56 m
36 kN
/m
4,0 m
E , I → constantes
2,0m2,0m18 kN

22. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 22 / 37
Desmembramento da estrutura em Caso (0) – Isostática Básica e Caso (1) , com seus respectivos
gráficos de momento fletor :
CASO (0)
90
04.3654
0
54
02.4.364.184.
0
18
018
0
1
1
2
2
1
1
1
=
=−+
=
=
=+−−
=
=
=+−
=
∑
∑
∑
V
V
V
V
V
H
H
H
R
R
F
R
R
M
R
R
F
X1
ϕ1R = 0
2
1
34
36 kN
/m
4,0 m
E , I → constantes
2,0m2,0m
18 kN
ϕ1018 kN
90 kN
54 kN
2
1
34
36 kN
/m
4,0 m
2,0m2,0m
18 kN

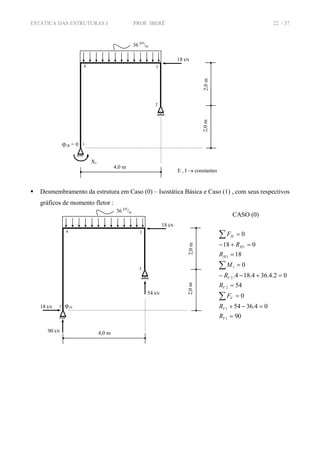
23. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 23 / 37
1,00
M0 [ kN.m ]
72,00
2
3
0
34
72,00
34
4
1
72,00
X1 . CASO (1)
4
1
1
4
1
1
4
1
2
2
1
1
0
0
014.
0
0
0
=
=−
=
=
=−+
=
=
=
∑
∑
∑
V
V
V
V
V
H
H
R
R
F
R
R
M
R
F
M1 [ kN.m ]
2
3
034
1,004
11,00
1,00
1,00
ϕ11
1
/4 kN
1
/4 kN
0
2
1
34
4,0 m
2,0m2,0m

24. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 24 / 37
Cálculo dos giros ϕ10 , ϕ11 , por Castigliano :
⎟
⎠
⎞
⎜
⎝
⎛
−−=== ∫∫ 2
..
3
..
3
..
.
.
1
...
.
1
.
.
.
10
10
10
kiskiskis
IE
dxMM
IE
dx
IE
MM
ϕ
IEIE .
144
2
72.1.4
3
72.1.4
3
72.1.4
.
.
1
10 +=⎟
⎠
⎞
⎜
⎝
⎛
++−=ϕ
⎟
⎠
⎞
⎜
⎝
⎛
+=== ∫∫ kis
kis
IE
dxMM
IE
dx
IE
MM
..
3
..
.
.
1
...
.
1
.
.
.
11
11
11ϕ
IEIE ..3
16
1.1.4
3
1.1.4
.
.
1
11 +=⎟
⎠
⎞
⎜
⎝
⎛
+=ϕ
Montagem sistema linear com equação de compatibilidade :
( R ) = ( 0 ) + X1 . ( 1 ) ⇒ 11110 .0 ϕϕ X+= ⇒
11
10
1
ϕ
ϕ
−=X
00,27
16
..3
.
144
1 −=⋅−=
IE
IE
X
∴ podemos assim afirmar que o momento reativo no engaste (1) assume o valor X1 . 1,0 kN.m ,
ou seja, vale 27,00 kN.m . O sinal negativo indica que o momento assume o sentido contrário ao
escolhido na proposição dos casos .
Cálculo das Reações de Apoio e Diagrama de Esforços Internos Solicitantes
( )1
41 90,00 27,00. 83,25VR kN= − + =
( )1 18,00 27,00. 0 18,00HR kN= − =
( )1
42 54,00 27,00. 60,75VR kN= − − =

25. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 25 / 37
83,25
83,25
–
–
60,75
60,75
0
N [ kN ]
83,25
60,75
V [ kN ]
+
1,69 m
18,00
18,00
–
–
0
45,00
51,26
M [ kN.m ]
1,69 m
27,00
45,00
0

26. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 26 / 37
EXERCÍCIO 07 : Na estrutura esquematizada abaixo , calcular as reações de apoio e
os diagramas de esforços internos solicitantes :
Resolução :
Definição da estrutura equivalente e numeração (Caso Real) :
13 kN
/m
4,0 m
E , I → constantes
2,5m2,5m
17 kN
4,0m1,0m
21 kN
X2
ϕ2R = 0 21
3 4
13 kN
/m
4,0 m
2,5m2,5m
17 kN
4,0m1,0m
21 kN
X1
δ1R = 0

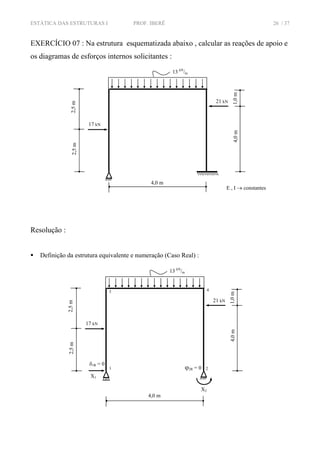
27. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 27 / 37
Desmembramento da estrutura em Caso (0) – Isostática Básica , Caso (1) e Caso (2) , com seus
respectivos gráficos de momento fletor :
CASO (0)
38,36
04.1362,15
0
62,15
04.212.4.135,2.174.
0
4
02117
0
1
1
2
2
1
2
2
=
=−+
=
=
=−++−
=
=
=+−+
=
∑
∑
∑
V
V
V
V
V
H
H
H
R
R
F
R
R
M
R
R
F
15,62 kN
4,00 kN
36,38 kN
ϕ20 21
3 4
13 kN
/m
4,0 m
2,5m2,5m
17 kN
4,0m1,0m
21 kN
δ10
M0 [ kN.m ]
26,00
1
3
0
3 4
42,50
3 4
4
2
42,50
1,00
20,00 4
2
21,00
0

28. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 28 / 37
X1 . CASO (1)
0
00
0
0
04.
0
1
01
0
1
1
2
2
1
2
2
=
=+
=
=
=+
=
=
=−
=
∑
∑
∑
V
V
V
V
V
H
H
H
R
R
F
R
R
M
R
R
F
0
1,00 kN
0
ϕ21
21
3 4
4,0 m
5,0m
δ11
1,00 kN
M1 [ kN.m ]
3 4
5,00 4
2
5,00
5,003
1
5,00

29. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 29 / 37
Cálculo dos giros ϕ20 , ϕ21 , ϕ22 , edas flechas δ10 , δ11 , δ12 , por Castigliano :
∫∫ == dxMM
IE
dx
IE
MM
...
.
1
.
.
.
10
10
10δ
( ) ( ) ( ) ⎥⎦
⎤
⎢⎣
⎡
−++−+++=
3
..
.2.
6
.
3
..
.
2
.
.2.
6
.
.
.
1
21212110
kis
kk
iskis
kk
is
kk
is
IE
δ
( ) ( ) ( )
IEIE .
02,192
3
5.20.5
45.2.
6
21.1
3
5.26.8
15,42.
2
5.4
5,25.2.
6
5,42.5,2
.
.
1
10 +=⎥⎦
⎤
⎢⎣
⎡
−++−+++=δ
⎟
⎠
⎞
⎜
⎝
⎛
++=== ∫∫ 3
..
..
3
..
.
.
1
...
.
1
.
.
.
11
11
11
kis
kis
kis
IE
dxMM
IE
dx
IE
MM
δ
X2 . CASO (2)
4
1
1
4
1
1
4
1
2
2
1
2
0
0
014.
0
0
0
=
=−
=
=
=−+
=
=
=
∑
∑
∑
V
V
V
V
V
H
H
R
R
F
R
R
M
R
F
0
1,00 kN.m
ϕ22
21
3 4
4,0 m
5,0m
δ12
1
/4 kN
1
/4 kN
M2 [ kN.m ]
3 4
0
4
2
1,00
1,00
3
1
1,00

30. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 30 / 37
IEIE .
33,183
3
5.5.5
5.5.4
3
5.5.5
.
.
1
11 +=⎟
⎠
⎞
⎜
⎝
⎛
++=δ
⎟
⎠
⎞
⎜
⎝
⎛
−−==== ∫∫ 2
..
2
..
.
.
1
...
.
1
.
.
.
21
21
2112
kiskis
IE
dxMM
IE
dx
IE
MM
ϕδ
IEIE .
50,22
2
5.1.5
2
1.5.4
.
.
1
2112 −=⎟
⎠
⎞
⎜
⎝
⎛
−−== ϕδ
( ) ⎥⎦
⎤
⎢⎣
⎡
−+++−=== ∫∫ 2
..
2
..
3
..
.2.
6
.
.
.
1
...
.
1
.
.
.
2120
20
20
kiskiskis
kk
is
IE
dxMM
IE
dx
IE
MM
ϕ
( )
IEIE .
50,44
2
1.21.1
2
1.20.5
3
26.1.4
5,421.2.
6
1.4
.
.
1
20 +=⎥⎦
⎤
⎢⎣
⎡
−+++−=ϕ
⎟
⎠
⎞
⎜
⎝
⎛
+=== ∫∫ kis
kis
IE
dxMM
IE
dx
IE
MM
..
3
..
.
.
1
...
.
1
.
.
.
22
22
22ϕ
IEIE .
33,6
1.1.5
3
1.1.4
.
.
1
22 +=⎟
⎠
⎞
⎜
⎝
⎛
+=ϕ
Montagem sistema linear com equação de compatibilidade :
( R ) = ( 0 ) + X1 . ( 1 ) + X2 . ( 2 ) ⇒
⎩
⎨
⎧
++=
++=
222211202
122111101
..
..
ϕϕϕϕ
δδδδ
XX
XX
R
R
⎪
⎪
⎩
⎪⎪
⎨
⎧
+−=
−+=
21
21
.
.
33,6
.
.
50,22
.
50,44
0
.
.
50,22
.
.
33,183
.
02,192
0
X
IE
X
IEIE
X
IE
X
IEIE
⇒
⎩
⎨
⎧
+−=−
−=−
21
21
.33,6.50,2250,44
.50,22.33,18302,192
XX
XX
⇒
⎩
⎨
⎧
−=
−=
074,19
388,3
2
1
X
X
∴ podemos assim afirmar que o momento reativo no engaste (2) assume o valor X2 . 1,0 kN.m , ou
seja, vale 19,07 kN.m ; e a reação horizontal no apoio (1) assume o valor X1 . 1,0 kN, ou seja , vale
3,39 kN. O sinais negativos indicam que o momento e a reação horizontal assumem o sentido
contrário ao escolhido na proposição dos casos .
Cálculo das Reações de Apoio e Diagrama de Esforços Internos Solicitantes
( )1
41 36,38 3,388.0 19,074. 31,61VR kN= − − + =
( )2 4,00 3,388. 1 19,074.0 7,39HR kN= − − − =
( )1
42 15,62 3,388.0 19,074. 20,39VR kN= − − − =

31. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 31 / 37
31,61
31,61
– –
20,39
20,39
N [ kN ]
–
13,61 13,61
31,61
–
3,39 V [ kN ]
+
+
13,61
2,43 m
–
+
3,39
13,61
13,61
7,39
20,39
13,617,39
–
19,07
3,14
8,48
M [ kN.m ]
25,55
1,57 m
10,49
3,14
25,55
12,86

32. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 32 / 37
EXERCÍCIO 08 : Na estrutura esquematizada abaixo , calcular as reações de apoio e
os diagramas de esforços internos solicitantes :
Resolução :
Definição da estrutura equivalente e numeração (Caso Real) :
20 kN
/m
4,0 m
E → constante
2,0m2,0m
40 kN
6,0m
2,0 m
I
I
I
2.I
X1
ϕ1R = 0
2
1
3 4
20 kN
/m
4,0 m
2,0m2,0m
40 kN
6,0m
I
I
2.I
40 kN
40 kN.m
X2
δ2R = 0

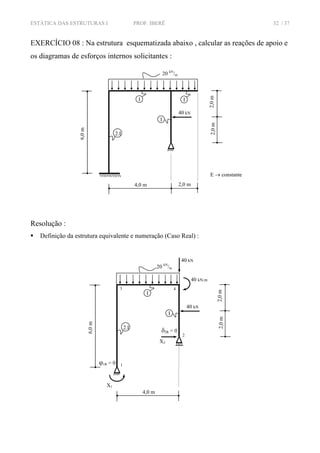
33. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 33 / 37
Desmembramento da estrutura em Caso (0) – Isostática Básica , Caso (1) e Caso (2) , com seus
respectivos gráficos de momento fletor :
CASO (0)
70
0404.2050
0
50
0404.402.4.204.404.
0
40
040
0
1
1
2
2
1
1
1
=
=−−+
=
=
=+++−−
=
=
=+−
=
∑
∑
∑
V
V
V
V
V
H
H
H
R
R
F
R
R
M
R
R
F
M0 [ kN.m ]
40,00
2
4
0
43
240,00
43
3
1
240,00
50 KN
40 KN
70 KN
ϕ10
2
1
3 4
20 KN
/m
4,0 m
2,0m2,0m
40 kN
6,0m
I
I
2.I
40 kN
40 kN.m
δ20
120,00
80,00

34. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 34 / 37
X1 . CASO (1)
4
1
1
4
1
1
4
1
2
2
1
1
0
0
014.
0
0
0
=
=−
=
=
=−+
=
=
=
∑
∑
∑
V
V
V
V
V
H
H
R
R
F
R
R
M
R
F
M1 [ kN.m ]
2
4
043
1,003
11,00
1,00
1,00 1
/4 kN
1
/4 kN
0 ϕ11
2
1
3 4
4,0 m
2,0m2,0m
6,0m
I
I
2.I
δ21

35. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 35 / 37
Cálculo dos giros ϕ10 , ϕ11 , ϕ12 , edas flechas δ20 , δ21 , δ22 , por Castigliano :
∫∫ +=
2
3
10
3
1
1010 ...
.
1
...
..2
1
dxMM
IE
dxMM
IE
ϕ ( ) ⎥⎦
⎤
⎢⎣
⎡
−++⎟
⎠
⎞
⎜
⎝
⎛
=
3
..
.2.
6
.
.
.
1
2
..
.
..2
1
21
kis
kk
is
IE
kis
IE
( )
IEIEIE ..3
2120
3
1.40.4
120240.2.
6
1.4
.
.
1
2
1.240.6
.
..2
1
10 =⎥⎦
⎤
⎢⎣
⎡
−++⎟
⎠
⎞
⎜
⎝
⎛
=ϕ
( ) ⎟
⎠
⎞
⎜
⎝
⎛
+=+= ∫∫ 3
..
.
.
1
...
..2
1
...
.
1
...
..2
1
2
3
10
3
1
1011
kis
IE
kis
IE
dxMM
IE
dxMM
IE
ϕ
( )
IEIEIE ..3
13
3
1.1.4
.
.
1
1.1.6.
..2
1
11 =⎟
⎠
⎞
⎜
⎝
⎛
+=ϕ
X2 . CASO (2)
5,0
05,0
0
5,0
02.14.
0
1
01
0
1
1
2
2
1
1
1
=
=+−
=
=
=+−
=
=
=−
=
∑
∑
∑
V
V
V
V
V
H
H
H
R
R
F
R
R
M
R
R
F
M2 [ kN.m ]
2
4
43
4,00
3
1
6,00
6,00
1,00
1,00 kN
0,5 kN
0,5 kN
ϕ12
2
1
3 4
4,0 m
2,0m2,0m
6,0m
I
I
2.I δ22
4,00

36. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 36 / 37
( )⎥⎦
⎤
⎢⎣
⎡
+−+⎟
⎠
⎞
⎜
⎝
⎛
−=+== ∫∫ 21
2
3
21
3
1
212112 .2.
6
.
.
.
1
2
..
.
..2
1
...
.
1
...
..2
1
kk
is
IE
kis
IE
dxMM
IE
dxMM
IE
δϕ
( )
IEIEIE ..3
59
46.2.
6
1.4
.
.
1
2
1.6.6
.
..2
1
2112 −=⎥⎦
⎤
⎢⎣
⎡
+−+⎟
⎠
⎞
⎜
⎝
⎛
−== δϕ
∫∫ +=
2
3
20
3
1
2020 ...
.
1
...
..2
1
dxMM
IE
dxMM
IE
δ
( ) ( ) ( )⎥⎦
⎤
⎢⎣
⎡
+−+++−++⎟
⎠
⎞
⎜
⎝
⎛
−= 21221221112120 .2.
6
.
..2....2.
6
.
3
.
.
.
1
3
..
.
..2
1
kk
is
kikikiki
s
kk
is
IE
kis
IE
δ
( ) ( ) ( )⎥⎦
⎤
⎢⎣
⎡
+−+++−++⎟
⎠
⎞
⎜
⎝
⎛
−= 24.2.
6
80.2
120.4.26.1204.240240.6.2.
6
4
46.
3
40.4
.
.
1
3
240.6.6
.
..2
1
20
IEIE
δ
IE..3
14560
20 −=δ
∫∫ +=
2
3
22
3
1
2222 ...
.
1
...
..2
1
dxMM
IE
dxMM
IE
δ ( )⎥
⎦
⎤
⎢
⎣
⎡
+++++⎟
⎠
⎞
⎜
⎝
⎛
= 22122111 ..2....2.
63
..
.
.
1
3
..
.
..2
1
kikikiki
skis
IE
kis
IE
( )
IEIEIE ..3
476
4.4.26.44.66.6.2.
6
4
3
4.4.4
.
.
1
3
6.6.6
.
..2
1
22 =⎥
⎦
⎤
⎢
⎣
⎡
+++++⎟
⎠
⎞
⎜
⎝
⎛
=δ
Montagem sistema linear com equação de compatibilidade :
( R ) = ( 0 ) + X1 . ( 1 ) + X2 . ( 2 ) ⇒
⎩
⎨
⎧
++=
++=
222211202
122111101
..
..
δδδδ
ϕϕϕϕ
XX
XX
R
R
⎪
⎪
⎩
⎪⎪
⎨
⎧
+−−=
−+=
21
21
.
..3
476
.
..3
59
..3
14560
0
.
..3
59
.
..3
13
..3
2120
0
X
IE
X
IEIE
X
IE
X
IEIE
⇒
⎩
⎨
⎧
+−=
−=−
21
21
.476.5914560
.59.132120
XX
XX
⇒
⎩
⎨
⎧
+=
−=
716,23
441,55
2
1
X
X
∴ podemos assim afirmar que o momento reativo no engaste (1) assume o valor X1 . 1,0 kN.m ,
ou seja, vale 55,44 kN.m , sendo que o sinal negativo indica que o momento assume sentido
contrário ao escolhido na proposição dos casos ; e a reação horizontal no apoio (2) assume o valor
X2 . 1,0 kN, ou seja , vale 23,72 kN , o sinal positivo indica que a reação horizontal assume o sentido
o escolhido na proposição dos casos .

37. ESTÁTICA DAS ESTRUTURAS I PROF. IBERÊ 37 / 37
Cálculo das Reações de Apoio e Diagrama de Esforços Internos Solicitantes
( )1 70,00 55,441.0,25 23,716. 0,50 44,28VR kN= − + − =
( )1 40,00 55,441.0 23,716. 1,00 16,28HR kN= − + − =
( )2 50,00 55,441. 0,25 23,716.0,50 75,72VR kN= − − + =
44,28
44,28
–
–
75,72
75,72
N [ kN ]
–
16,28 16,28
0
44,28
–
16,28
V [ kN ]
+
+
23,72
2,21 m
–
+
40,00
16,28
35,72
16,28
23,72
16,28
–
47,44
25,12
55,44
M [ kN.m ]
42,24
2,21 m
14,88
40,00
42,24
6,78