O documento apresenta exercícios resolvidos sobre elementos geométricos de estradas, curvas horizontais circulares e locação de curvas. Os exercícios envolvem cálculos de comprimentos, ângulos, raios, deflexões e locação de pontos de curva e tangente.






















![Glauco Pontes Filho 31
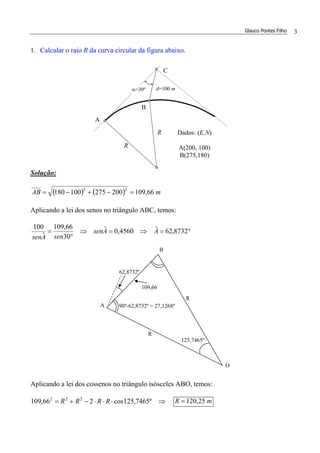
1. Calcular as curvas de transição abaixo:
a) E(PI) = 342 + 2,50 ∆ = 55º Rc= 680 m V= 80 km/h
b) E(PI) = 1350 + 12,73 ∆ = 12º Rc=2100 m V=120 km/h
c) E(PI) = 476 + 9,50 ∆ = 66º24' Rc= 830 m V=100 km/h
d) E(PI) = 757 + 6,75 ∆ = 82º Rc= 600 m V= 70 km/h
Solução:
a) m
R
V
Lsmín 11,27
680
80
036,0036,0
33
=⋅==
m
R
Ls c
máx 75,652
180
55680
180
=
°
⋅°⋅
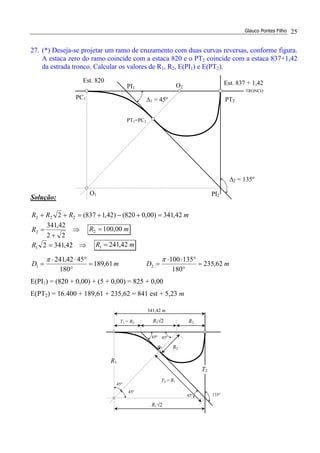
=
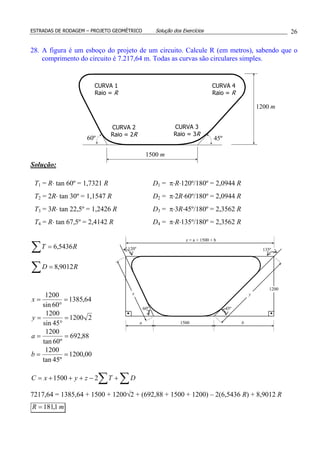
°
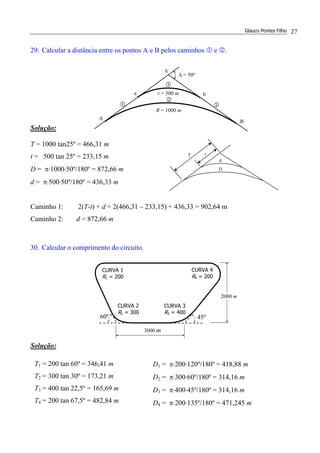
⋅∆⋅
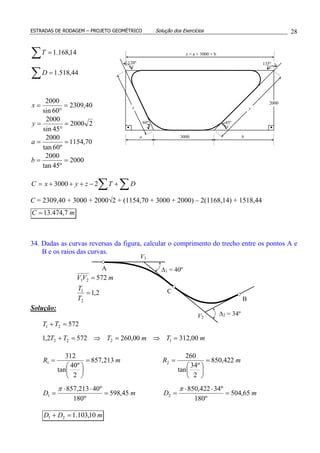
=
ππ
Adotando Ls = 120 m (>0,56V), temos:
( ) [ ]
( ) ( ) mpRkTT
mradRYp
mradsensenRXk
mradRD
rad
mLY
mLX
rad
R
L
c
scs
scs
radc
s
ss
ss
ss
ss
c
s
s
43,414
2
55
tan88,068098,59
2
tan
88,0)088235,0cos(168053,3cos1
98,59)088235,0(68091,119
75,532)783461,0(680
783461,0)088235,0(2
180
552
53,3
42
088235,0
3
088235,0
120
423
91,119
216
088235,0
10
088235,0
1120
21610
1
088235,0
6802
120
2
33
4242
=
°
⋅++=
∆
⋅++=
=−⋅−=−⋅−=
=⋅−=⋅−=
=⋅=⋅=
=⋅−
°
⋅°=⋅−∆=
=
−⋅=
−⋅=
=
+−⋅=
+−⋅=
=
⋅
=
⋅
=
θ
θ
φ
π
θφ
θθ
θθ
θ
E(TS) = E(PI) – [TT] = (342 + 2,50) – (20 + 14,43) = 321 + 8,07
E(SC) = E(TS) + [LS] = (321 + 8,07) + (6 + 0,00) = 327 + 8,07
E(CS) = E(SC) + [D] = (327 + 8,07) + (26 + 12,75) = 354 + 0,82
E(ST) = E(CS) + [LS] = (354 + 0,82) + (6 + 0,00) = 360 + 0,82](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-31-320.jpg)



![Glauco Pontes Filho 35
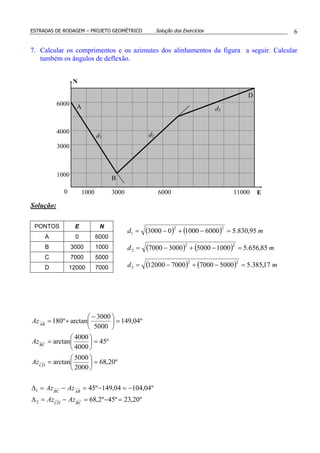
3. Numa curva de transição, para a determinação do comprimento de transição (Ls) foi
escolhido o valor J = 0,4 m/s3
(variação da aceleração centrífuga por unidade de tempo).
Calcular a estaca do ST. Dados: ∆ = 50º, Rc = 500 m, Vp = 100 km/h e E(PI) = 210 + 0,00.
Solução:
m
JR
V
L
LR
V
J
c
s
sc
17,107
5004,0
6,3
100
3
33
=
⋅
=
⋅
=⇒
⋅
=
rad
R
L
c
s
s 10717,0
5002
17,107
2
=
⋅
=
⋅
=θ
mLX ss
ss 05,107
216
10717,0
10
10717,0
117,107
21610
1
4242
=
+−⋅=
+−⋅=
θθ
mLY ss
ss 83,3
42
10717,0
3
10717,0
17,107
423
33
=
−⋅=
−⋅=
θθ
rads 658327,0)10717,0(2
180
502 =⋅−
°
⋅°=⋅−∆=
π
θφ
mestmradRD radc 16,91616,329)658327,0(500 +==⋅=⋅= φ
mradsensenRXk scs 56,53)10717,0(50005,107 =⋅−=⋅−= θ
( ) [ ] mradRYp scs 96,0)10717,0cos(150083,3cos1 =−⋅−=−⋅−= θ
( ) ( ) 16,71416,287
2
50
tan96,050056,53
2
tan +==
°
⋅++=
∆
⋅++= mpRkTT c
E(TS) = E(PI) – [TT] = (210 + 0,00) – (14 + 7,16) = 195 + 12,84
E(SC) = E(TS) + [LS] = (195 + 12,84) + (5 + 7,17) = 201 + 0,01
E(CS) = E(SC) + [D] = (201 + 0,01) + (16 + 9,16) = 217 + 9,17
E(ST) = E(CS) + [LS] = (217 + 9,17) + (5 + 7,17) = 222 + 16,34](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-35-320.jpg)

![Glauco Pontes Filho 37
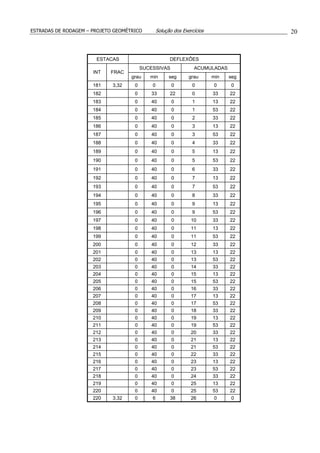
CÁLCULO DA CURVA 2:
m
JR
smV
Ls 07,108
330559,0600
6,3
100
)/(
3
22
3
2 =
⋅
=
⋅
=
rads 090058,0
6002
07,108
=
⋅
=θ
rads 518017,0)090058,0(2
180
402 =⋅−
°
⋅°=⋅−∆=
π
θφ
mLX ss
ss 98,107
216
090058,0
10
090058,0
107,108
21610
1
4242
=
+−⋅=
+−⋅=
θθ
mLY ss
ss 24,3
42
090058,0
3
090058,0
07,108
423
33
=
−⋅=
−⋅=
θθ
mestmradRD radc 81,101581,310)518017,0(600 +==⋅=⋅= φ
mradsensenRXk scs 02,54)090058,0(60098,107 =⋅−=⋅−= θ
( ) [ ] mradRYp scs 81,0)090058,0cos(160024,3cos1 =−⋅−=−⋅−= θ
( ) ( ) 70,121370,272
2
40
tan81,060002,54
2
tan +==
°
⋅++=
∆
⋅++= mpRkTT c
E(TS2) = E(PI2) – [TT2] = (91 + 10,00) – (13 + 12,70) = 77 + 17,30
Como o início da segunda curva deve ser depois do fim da primeira (ou coincidirem), não
é possível projetar a curva 2 com o J da curva 1, pois :
E(TS2)=77+17,30 < E(ST1)=104+4,25.
PI2
PI1
TS2
ST1
TS2 < ST1 ???
Impossível !!!](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-37-320.jpg)

![Glauco Pontes Filho 39
mLY ss
ss 726,7
42
235381,0
3
235381,0
86,98
423
33
=
−⋅=
−⋅=
θθ
Letra a) 3
3
3
/53,0
86,98210
6,3
80
sm
LR
V
J
sc
=
⋅
=
⋅
=
Letra b) ( ) [ ] mradRYp scs 94,1)235381,0cos(1210726,7cos1 =−⋅−=−⋅−= θ
Letra c) rads 052838,0)235381,0(2
180
302 =⋅−
°
⋅°=⋅−∆=
π
θφ
mradRD radc 10,11)052838,0(210 =⋅=⋅= φ
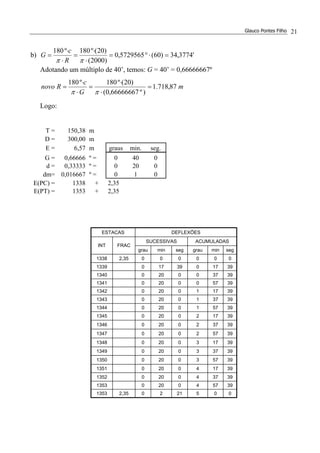
8. (*) Dado o alinhamento da figura, sendo o raio da curva 1 igual a 500 m e fixada a
velocidade de projeto Vp=72 km/h, calcular as estacas dos pontos TS1, SC1, CS1, ST1, PC2,
PT2 e estaca final do trecho, respeitando as seguintes condições: a) a curva 1 terá transições
simétricas de comprimento Ls, calculado para uma variação de aceleração centrífuga por
unidade de tempo J=0,2 m/s3
; b) a curva 2 será uma curva circular sem transições; c) entre
o ST1 e o PC2 existe um trecho em tangente de comprimento 200 m; d) a curva 2 terá o
maior raio possível, respeitadas as condições a, b e c.
Solução:
CÁLCULO DA CURVA 1:
m
JR
V
L
LR
V
J
c
s
sc
80
5002,0
6,3
72
3
33
=
⋅
=
⋅
=⇒
⋅
=
rad
R
L
c
s
s 08,0
5002
80
2
=
⋅
=
⋅
=θ
452,66 m
∆2=24º
∆1=24º
CURVA 2
1000 m
PI2
1000 m
PI1
EST. 0
CURVA 1
F](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-39-320.jpg)
![ESTRADAS DE RODAGEM – PROJETO GEOMÉTRICO Solução dos Exercícios 40
mLX ss
ss 95,79
216
08,0
10
08,0
180
21610
1
4242
=
+−⋅=
+−⋅=
θθ
mLY ss
ss 13,2
42
08,0
3
08,0
80
423
33
=
−⋅=
−⋅=
θθ
rads 258880,0)08,0(2
180
242 =⋅−
°
⋅°=⋅−∆=
π
θφ
mestmradRD radc 44,9644,129)258880,0(500 +==⋅=⋅= φ
mradsensenRXk scs 99,39)08,0(50095,79 =⋅−=⋅−= θ
( ) [ ] mradRYp scs 53,0)08,0cos(150013,2cos1 =−⋅−=−⋅−= θ
( ) ( ) 38,6738,146
2
24
tan53,050099,39
2
tan +==
°
⋅++=
∆
⋅++= mpRkTT c
E(TS) = E(PI) – [TT] = (50 + 0,00) – (7 + 6,38) = 42 + 13,62
E(SC) = E(TS) + [LS] = (42 + 13,62) + (4 + 0,00) = 46 + 16,32
E(CS) = E(SC) + [D] = (46 + 16,32) + (6 + 9,44) = 53 + 3,06
E(ST) = E(CS) + [LS] = (53 + 3,06) + (4 + 0,00) = 57 + 3,06
CÁLCULO DA CURVA 2:
E(PC2) = E(ST1) + 200 m =(57 + 3,06) + (10 + 0,00) = 67 + 3,06 = 1.343,06 m
T = 452,66 – TT – 200 = 452,66 – 146,38 – 200 = 106,28 m
m
T
R 01,500
2
º24
tan
28,106
2
tan 2
=
=
∆
=
mD 44,209
180
2401,500
=
°
°⋅⋅
=
π
E(PT2) = E(PC2) + D = 1.343,06 + 209,44 = 1.552,50 m = 77 + 12,50
E(F) = E(PT2) + 1000m - T = 1.552,50 + 1.000 – 106,28 = 2.446,22 m =122 + 6,22](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-40-320.jpg)
![Glauco Pontes Filho 41
9. (*) Dada a curva horizontal da figura, calcular os valores de X e Y do ponto P que está na
estaca 100 + 0,00. Dados: Rc = 350 m, E(PI) = 90 + 15,00, Ls = 150 m e ∆ = 60º.
Solução: rad
R
L
c
s
s 214286,0
3502
150
2
=
⋅
=
⋅
=θ
mLX ss
ss 31,149
216
214286,0
10
214286,0
1150
21610
1
4242
=
+−⋅=
+−⋅=
θθ
mLY ss
ss 68,10
42
214286,0
3
214286,0
150
423
33
=
−⋅=
−⋅=
θθ
rads 618626,0)214286,0(2
180
602 =⋅−
°
⋅°=⋅−∆=
π
θφ
52,161052,216)618626,0(350 +==⋅=⋅= mradRD radc φ
mradsensenRXk scs 89,74)214286,0(35031,149 =⋅−=⋅−= θ
( ) [ ] mradRYp scs 674,2)214286,0cos(135068,10cos1 =−⋅−=−⋅−= θ
( ) ( ) 50,181350,278
2
60
tan674,235089,74
2
tan +==
°
⋅++=
∆
⋅++= mpRkTT c
E(TS) = E(PI) – [TT] = (90 + 15,00) – (13 + 18,50) = 76 + 16,50
E(SC) = E(TS) + [LS] = (76 + 16,50) + ( 7 + 10,00) = 84 + 6,50
E(CS) = E(SC) + [D] = (84 + 6,50) + (10 + 16,52) = 95 + 3,02
E(ST) = E(CS) + [LS] = (95 + 3,02) + ( 7 + 10,00) = 102 + 13,02
L = (102 + 13,02) – (100 + 0,00)
L = 2 est + 13,02 m = 53,02 m
rad
LR
L
sc
026773,0
1503502
02,53
2
22
=
⋅⋅
=
⋅⋅
=θ
mLX 02,53
216
026773,0
10
026773,0
102,53
21610
1
4242
=
+−⋅=
+−⋅=
θθ
mLY 47,0
42
026773,0
3
026773,0
02,53
423
33
=
−⋅=
−⋅=
θθ
ST
CS
L
60º
95+3,02
102+13,02
100+0,00](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-41-320.jpg)
![ESTRADAS DE RODAGEM – PROJETO GEOMÉTRICO Solução dos Exercícios 42
10. (*) Deseja-se projetar uma curva de transição com J = 0,4 m/s3
. Calcular a deflexão que
deve ser dada no aparelho (colocado sobre o TS) para locar a estaca 200. Dados: Vp=100
km/h, ∆=40º, Rc=600 m, E(PI) = 209 + 3,23.
Solução: m
JR
V
L
LR
V
J
c
s
sc
31,89
6004,0
6,3
100
3
33
=
⋅
=
⋅
=⇒
⋅
=
rad
R
L
c
s
s 074425,0
6002
31,89
2
=
⋅
=
⋅
=θ
mLX ss
ss 26,89
216
074425,0
10
074425,0
131,89
21610
1
4242
=
+−⋅=
+−⋅=
θθ
mLY ss
ss 21,2
42
074425,0
3
074425,0
31,89
423
33
=
−⋅=
−⋅=
θθ
rads 549283,0)074425,0(2
180
402 =⋅−
°
⋅°=⋅−∆=
π
θφ
mestmradRD radc 57,91657,329)549283,0(600 +==⋅=⋅= φ
mradsensenRXk scs 65,44)074425,0(60026,89 =⋅−=⋅−= θ
( ) [ ] mradRYp scs 554,0)074425,0cos(160021,2cos1 =−⋅−=−⋅−= θ
( ) ( ) 23,31323,263
2
40
tan554,060065,44
2
tan +==
°
⋅++=
∆
⋅++= mpRkTT c
E(TS) = E(PI) – [TT] = (209 + 3,23) – (13 + 3,23) = 196 + 0,00
E(SC) = E(TS) + [LS] = (196 + 0,00) + ( 4 + 9,31) = 200 + 9,31
E(CS) = E(SC) + [D] = (200 + 9,31) + (16 + 9,57) = 216 + 18,87
E(ST) = E(CS) + [LS] = (216 + 18,87) + ( 4 + 9,31) = 221 + 8,18
L = (200 + 0,00) – (196 + 0,00) = 4 est + 0,00 m = 80 m
rad
LR
L
sc
029618,0
17,1075002
34,56
2
22
=
⋅⋅
=
⋅⋅
=θ
mLX 335,56
216
029618,0
10
029618,0
134,56
21610
1
4242
=
+−⋅=
+−⋅=
θθ
mLY 56,0
42
029618,0
3
029618,0
34,56
423
33
=
−⋅=
−⋅=
θθ
ST
CS
L
50º
217+9,17
222+16,34
220+0,00](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-42-320.jpg)
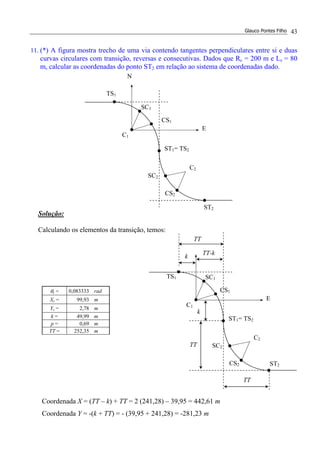


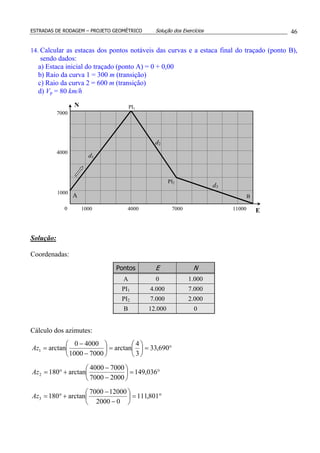
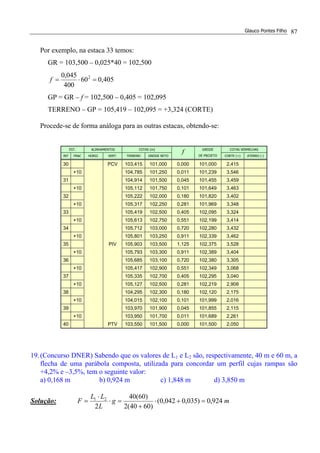
![Glauco Pontes Filho 47
Cálculo dos ângulos centrais:
∆1 = Az2 – Az1 = 149,036° - 33,690° = 115,346°
∆2 = | Az3 – Az2 | = 149,036° - 111,801° = 37,235°
Cálculo dos comprimentos dos alinhamentos:
( ) ( ) md 10,211.77000100004000
22
1 =−+−=
( ) ( ) md 95,830.52000700070004000
22
2 =−+−=
( ) ( ) md 16,385.502000120007000
22
3 =−+−=
Cálculo da curva 1 (transição):
Lsmin = 0,036⋅ (80)3/300 = 61,44 m
Lsmax = 300⋅(115,346º)⋅(3,1416)/180º = 603,95 m
Adotando Ls = 200 m (>0,56V) (o leitor pode adotar outro valor), temos:
E(PI1) = [d1] = 360 est + 11,10 m
R1 = 300 m
AC1 = ∆1 = 115,346°
Ls = 200 m
θs1 = 0,166667 rad
Xs1 = 99,72 m
Ys1 = 5,54 m
k1 = 49,95 m
p1 = 1,39 m
TT1 = 526,20 m
φ 1= 1,679838 rad
D1= 503,95 m
E(TS1) = 334 + 4,90
E(SC1) = 339 + 4,90
E(CS1) = 364 + 8,85
E(ST1) = 369 + 8,85
Cálculo da curva 2 :](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-47-320.jpg)
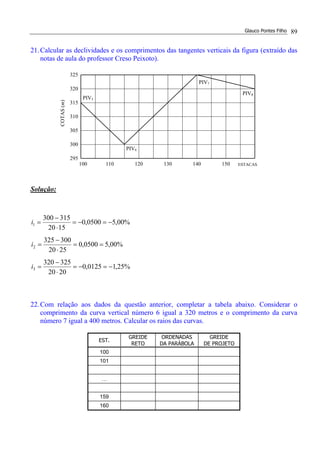
![ESTRADAS DE RODAGEM – PROJETO GEOMÉTRICO Solução dos Exercícios 48
R2 = 600 m
∆2 = 37,235°
E(PI2) = E(ST1) + [d2] – [TT1]
E(PI2) = 7.388,85 + 5830,95 – 526,20 = 12.693,60 m= 634 est + 13,60 m
Lsmin = 0,036⋅ (80)3/600 = 30,72 m
Lsmax = 600⋅(37,235º)⋅(3,1416)/180º = 389,93 m
Adotando Ls = 100 m (>0,56V) (o leitor pode adotar outro valor), temos:
θs2 = 0,083333 rad
Xs2 = 99,93 m
Ys2 = 2,78 m
k2 = 49,99 m
p2 = 0,69 m
TT2 = 252,35 m
φ 2 = rad
D2 = 289,92 m
E(TS2) = 622 + 1,25
E(SC2) = 627 + 1,25
E(CS2) = 641 + 11,18
E(ST2) = 646 + 11,18
Estaca final do traçado (ponto B):
E(B) = E(ST2) + [d3] – [TT2]
E(B) = 12.931,18 + 5.385,16 – 252,35 = 18.063,99 = 903 est + 3,99 m](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-48-320.jpg)


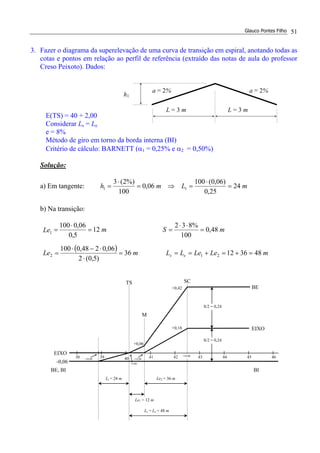

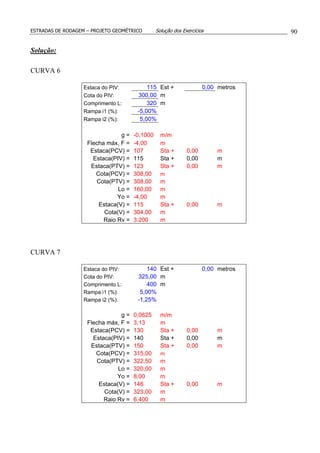
![Glauco Pontes Filho 53
1. Calcular a superlargura, sendo dados os seguintes elementos:
Largura do veículo: L = 2,50 m.
Distância entre os eixos do veículo: E = 6,50 m.
Distância entre a frente do veículo e o eixo dianteiro: F = 1,10 m.
Raio da curva: R = 280 m.
Velocidade de projeto: V = 90 km/h.
Faixas de tráfego de 3,3 m (LB = 6,6 m).
Número de faixas: 2.
Solução: Tabela 7.1: LB = 6,6 m → GL = 0,75 m.
( ) [ ]
( ) 6,6538,0028,0)75,0575,2(22
538,0
28010
90
10
028,0280)5,6(210,110,12802
575,2
)280(2
5,6
50,2
2
22
22
−+++⋅=−+++⋅=
===
=−⋅+⋅+=−+⋅+=
=
⋅
+=
⋅
+=
BDFLC
D
F
C
LFGGGS
m
R
V
F
mREFFRG
m
R
E
LG
Steórico = 0,62 m
Sprático = 0,80 m (múltiplo de 0,20 m)
2. Idem, para:
Largura do veículo: L = 2,50 m.
Distância entre os eixos do veículo: E = 6,10 m.
Distância entre a frente do veículo e o eixo dianteiro: F = 1,20 m.
Raio da curva: R = 200 m.
Velocidade de projeto: V = 80 km/h.
Faixas de tráfego de 3,6 m (LB = 7,2 m).
Número de faixas: 2.
Solução: Tabela 7.1: LB = 7,2 m → GL = 0,90 m.
( ) [ ]
( ) 2,7566,0040,0)90,0593,2(22
566,0
20010
80
10
040,0200)10,6(220,120,12002
593,2
)200(2
1,6
50,2
2
22
22
−+++⋅=−+++⋅=
===
=−⋅+⋅+=−+⋅+=
=
⋅
+=
⋅
+=
BDFLC
D
F
C
LFGGGS
m
R
V
F
mREFFRG
m
R
E
LG
Steórico = 0,39 m
Sprático = 0,40 m (múltiplo de 0,20 m)](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-53-320.jpg)
![ESTRADAS DE RODAGEM – PROJETO GEOMÉTRICO Solução dos Exercícios 54
3. Idem, para:
Largura do veículo: L = 2,40 m.
Distância entre os eixos do veículo: E = 7,0 m.
Distância entre a frente do veículo e o eixo dianteiro: F = 1,40 m.
Raio da curva: R = 180 m.
Velocidade de projeto: V = 100 km/h.
Faixas de tráfego de 3,6 m (LB = 7,2 m).
Número de faixas: 2.
Solução: Tabela 7.1: LB = 7,2 m → GL = 0,90 m.
( ) [ ]
( ) 2,77454,00599,0)90,05361,2(22
7454,0
18010
100
10
0599,0180)7(240,140,11802
5361,2
)180(2
7
40,2
2
22
22
−+++⋅=−+++⋅=
===
=−⋅+⋅+=−+⋅+=
=
⋅
+=
⋅
+=
BDFLC
D
F
C
LFGGGS
m
R
V
F
mREFFRG
m
R
E
LG
Steórico = 0,48 m
Sprático = 0,60 m (múltiplo de 0,20 m)
4. Calcular a superlargura necessária numa curva:
a) R = 250 m; LB = 7,20 m; V = 100 km/h (Veículo SR).
b) R = 280 m; LB = 7,00 m; V = 90 km/h (Veículo CO).
Solução: a) mSteórico 88,020,0250
25010
100
250
100
25044,25 2
=−−+++=
Sprático = 1,00 m (múltiplo de 0,20 m)
b) Tabela 7.1: LB = 7,0 m → GL = 0,90 m.
( ) [ ]
( ) 0,75379,00287,0)90,06664,2(22
5379,0
28010
90
10
0287,0280)1,6(220,120,12802
6664,2
)280(2
1,6
60,2
2
22
22
−+++⋅=−+++⋅=
===
=−⋅+⋅+=−+⋅+=
=
⋅
+=
⋅
+=
BDFLC
D
F
C
LFGGGS
m
R
V
F
mREFFRG
m
R
E
LG
Steórico = 0,70 m
Sprático = 0,80 m (múltiplo de 0,20 m)](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-54-320.jpg)



![ESTRADAS DE RODAGEM – PROJETO GEOMÉTRICO Solução dos Exercícios 58
E(V) = E(PCV) + [L0] = (70+ 0,00) + (2+ 0,00) = 72 est + 0,00 m
myPCVCotaVCota 40,66920,020,669)()( 0 =+=+=
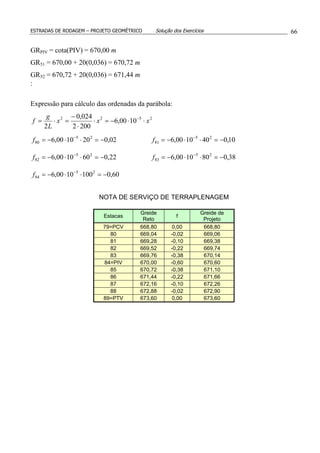
Expressão para cálculo das ordenadas da parábola:
222
000125,0
1602
04,0
2
xxx
L
g
f ⋅=⋅
⋅
=⋅=
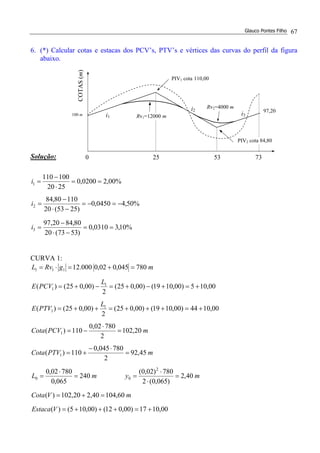
800,080000125,0
450,060000125,0
200,040000125,0
050,020000125,0
00000125,0
2
74
75
2
73
76
2
72
77
2
71
78
2
70
=⋅=
==⋅=
==⋅=
==⋅=
==⋅=
f
ff
ff
ff
ffestaca
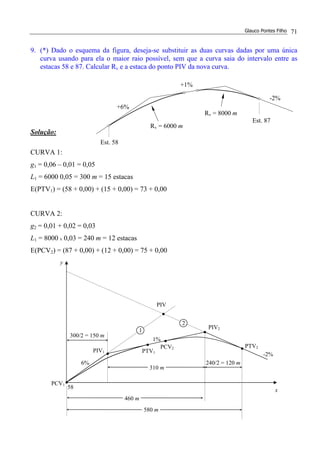
NOTA DE SERVIÇO SIMPLIFICADA
EST. COTAS DO
GREIDE DE
PROJETO
ORDENADAS
DA PARÁBOLA
GREIDE
DE PROJETO
70=PCV 669,20 0,00 669,20
71 669,40 0,05 669,35
72 669,60 0,20 669,40
73 669,80 0,45 669,35
74=PIV 670,00 0,80 669,20
75 669,40 0,45 668,95
76 668,80 0,20 668,60
77 668,20 0,05 668,15
78=PTV 667,60 0,00 667,60](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-58-320.jpg)

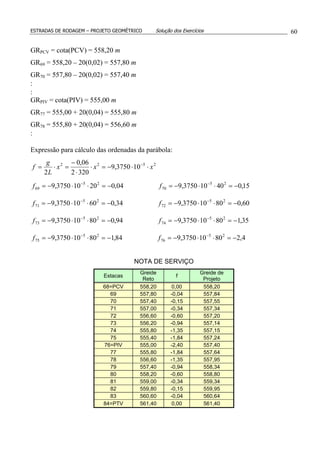
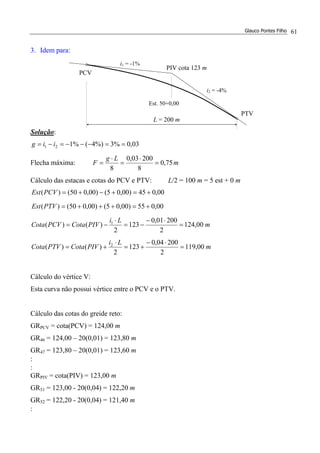
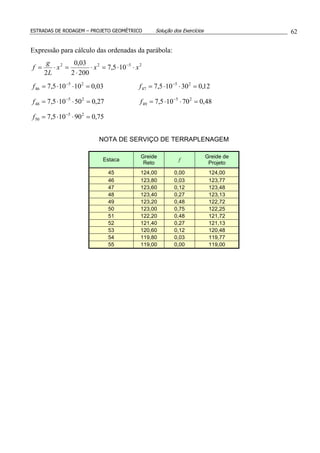
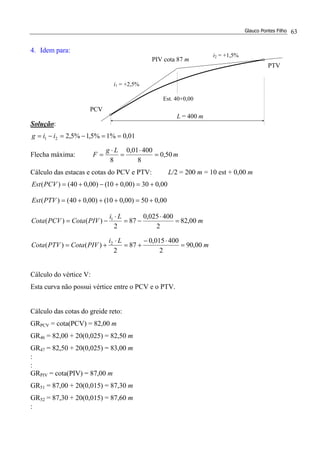

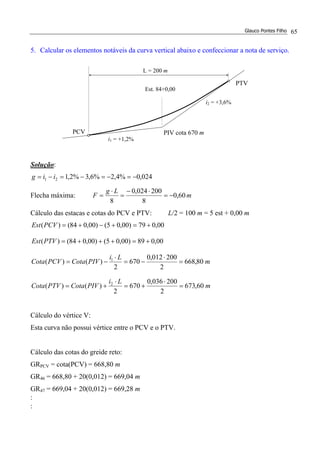







![ESTRADAS DE RODAGEM – PROJETO GEOMÉTRICO Solução dos Exercícios 76
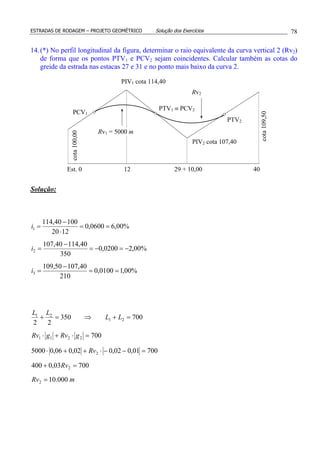
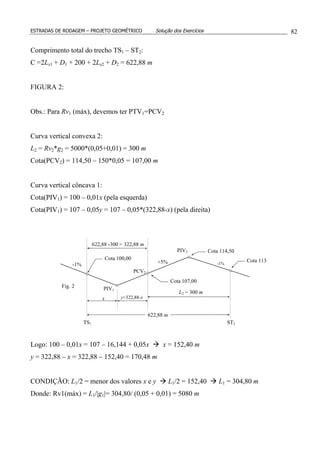
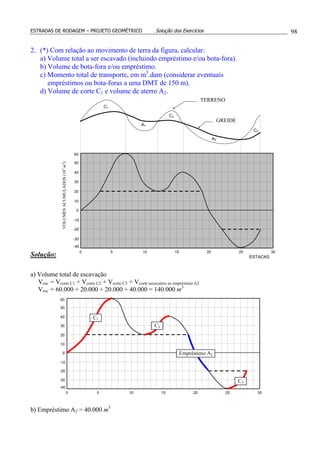
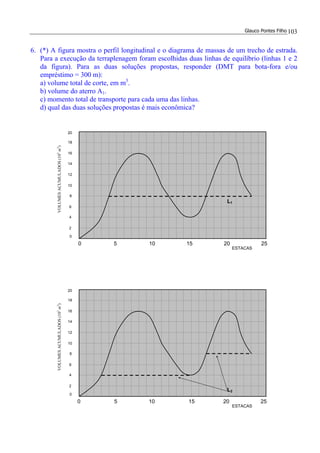
12.(*) A figura mostra o perfil longitudinal de uma estrada onde as duas rampas intermediárias
têm inclinação de –2,5% e +2,5%, respectivamente. Determinar estaca e cota do PIV2.
Solução:
Cota(PIV1) = 804,12 + 0,02 (2.734) = 858,80 m
Cota(PIV3) = 869,10 - 0,01 (3.398) = 835,12 m
Cota(PIV2) = Cota(PIV1) – 0,025x = Cota(PIV3) – 0,025 y
Logo: 858,80 – 0,025x = 835,12 – 0,025 y x – y = 947,20
x + y = 2.244,00
Donde: x = 1.595,60 m e y = 648,40 m
Cota(PIV2) = Cota(PIV1) – 0,025x = 858,80 – 0,025 (1595,60) = 818,91 m
E(PIV2) = E(PIV1) + [x] = (136 + 14,00) + (79 + 15,60) = 216 + 9,60
PIV3
PIV2
+2,5%
+2%
+1%
-2,5%
PIV1
418+16,00248+18,00?136+14,00Est. 0
cota 804,12 m
x y
cota 869,10 m
2.734 m 3.398 m
x+y=2.244 m](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-76-320.jpg)


![ESTRADAS DE RODAGEM – PROJETO GEOMÉTRICO Solução dos Exercícios 80
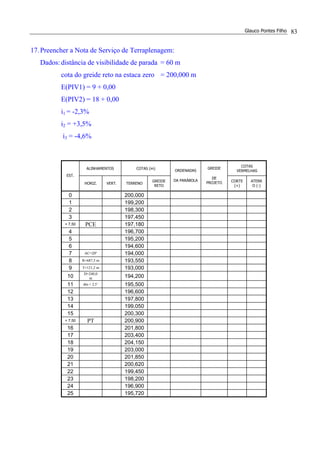
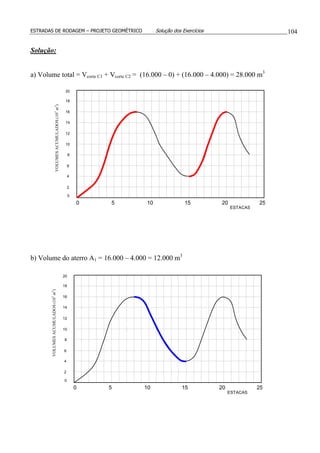
15.(*) Dado o perfil longitudinal da figura, calcular a rampa i2 de forma que ela tenha a menor
inclinação possível. Os raios mínimos das curvas verticais são iguais a 4000 m.
Solução:
[ ]
[ ] [ ]
1875,00200,0
0158304000
950)02,0(2000)01,0(2000)02,0(40486)01,0(20500
:21
)2()02,0(40486)01,0(20500
)()(
)02,0(4048602,0
2
486)(
)01,0(2050001,0
2
500)(
)1(950)02,0(2000)01,0(2000
950
22
)02,0(400002,04000
)01,0(400001,04000
22
2
2
2
22222
222
221
2
2
2
2
1
1
22
21
22222
22111
−=−=
=++
+−⋅−−⋅−⋅−=−⋅−−−⋅+
⋅−=−⋅−−−⋅+
⋅−=−=
−⋅−=⋅−=
−⋅+=⋅+=
=+−⋅−−⋅−
=++
−⋅=−⋅=⋅=
−⋅=−⋅=⋅=
ioui
ii
iiiii
emdoSubstituin
equaçãoxiii
xiPIVCotaPIVCotah
i
L
PIVCota
i
L
PIVCota
equaçãoxii
L
x
L
iigRvL
iigRvL
Logo: %22 −=i
x
i2
+1% +2%Estaca0
950 m
cota500
Est.47+10,00
cota486
L1/2 h](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-80-320.jpg)



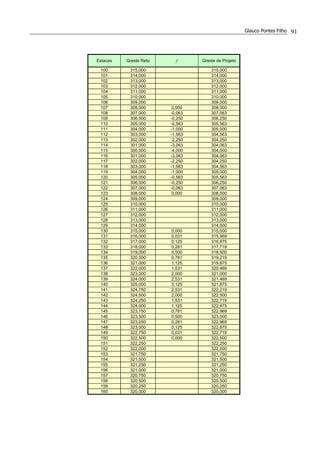



![ESTRADAS DE RODAGEM – PROJETO GEOMÉTRICO Solução dos Exercícios 100
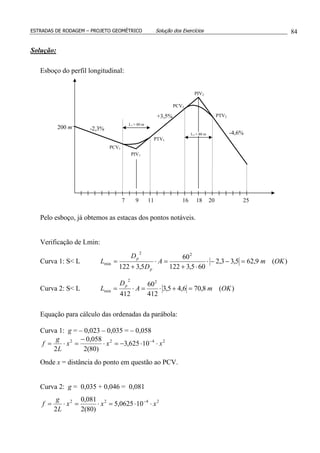
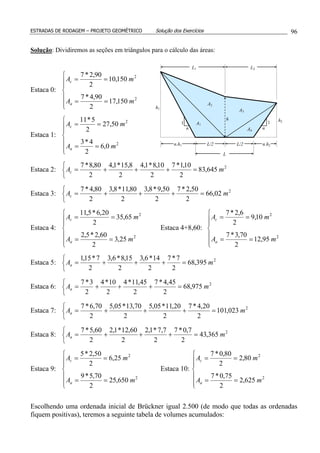
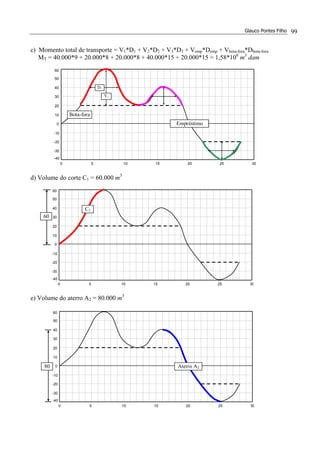
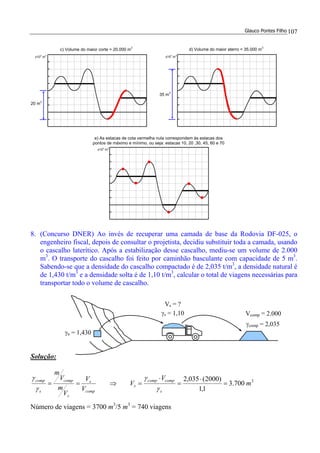
3. (*) Para execução do movimento de terra da figura, foi escolhida para linha de equilíbrio
(LE) a horizontal tracejada da figura. Sabendo-se que os eventuais bota-foras e/ou
empréstimos terão uma distância de transporte de 10 dam, calcular:
a) quantos m3
serão transportados do corte C1 para o aterro A1.
b) volume do corte C1.
c) volume total a ser escavado para a execução dos serviços.
d) momento de transporte total, em m3
.dam
Solução:
a) [-2-(-8)]*103
= 6.000 m3
0
ESTACAS
VOLUMESACUMULADOS(103
m3
)
-7
-6
-5
-4
-3
-2
-1
0
1
-8
2
5 10 15 20 25 30
C1
A1
C2
A2
A3
TERRENO
GREIDE
LE
0
ESTACAS
VOLUMESACUMULADOS(103
m3
)
-7
-6
-5
-4
-3
-2
-1
0
1
-8
2
5 10 15 20 25 30
C1
A1
C2A2
A3
TERRENO
GREIDE
LE](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-100-320.jpg)
![Glauco Pontes Filho 101
b) Vcorte C1 = [2-(-8)] )]*103
= 10.000 m3
c) Vescavação = Vcorte C1 + Vcorte C2 + Vcorte para empréstimo = 10.000 + 6.000 + 2.000 = 18.000 m3
d) MT = V1*D1+V2*D2+V3*D3+V4*D4+Vemp*Demp = 6000*12+4000*8+4000*8,6+2000*4+2000*10
MT = 1,66*105
m3
.dam
0
ESTACAS
VOLUMESACUMULADOS(103
m3
)
-7
-6
-5
-4
-3
-2
-1
0
1
-8
2
5 10 15 20 25 30
LE
0
ESTACAS
VOLUMESACUMULADOS(103
m3
)
-7
-6
-5
-4
-3
-2
-1
0
1
-8
2
5 10 15 20 25 30
LE
Empréstimo
Corte C1
Corte C2
0
ESTACAS
VOLUMESACUMULADOS(103
m3
)
-7
-6
-5
-4
-3
-2
-1
0
1
-8
2
5 10 15 20 25 30
LE
V1
D1
D1 = 12 dam
D2 = 8 dam
D3 = 8,6 dam
D4 = 4 dam
Empréstimo](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-101-320.jpg)


![ESTRADAS DE RODAGEM – PROJETO GEOMÉTRICO Solução dos Exercícios 108
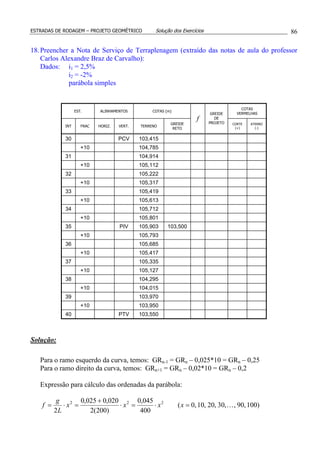
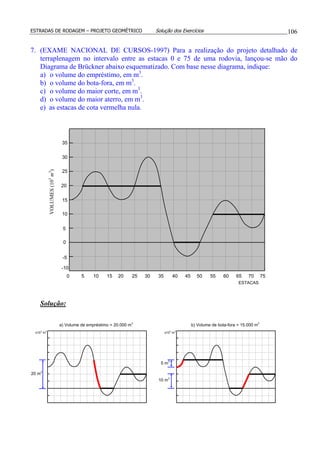
9. Calcular a área da
seção transversal da figura.
Solução:
uaA
A
A
50,40
3122415104309
2
1
0054630
3362153
2
1
=
+−−−+−−−⋅=
−−−−
⋅=
10.Calcular o volume do prismóide.
( )21 4
6
AAA
L
V m +⋅+⋅=
Solução:
[ ] 3
33,853.2100)144(4180
6
20
mV =+⋅+⋅=
11.Com relação à questão anterior, qual o erro cometido se o volume fosse calculado pela
fórmula das áreas médias V = L.(A1 + A2)/2 ?
Solução: ( ) 3
800.2100180
2
20
mV =+⋅=
Erro de -53,33 m3
ou -1,87%
(0,0)(-3,0)
(-5,3)
(-1,6)
(2,4)
(6,5)
(3,0)
L = 20 m
Am = 144 m2
A1 = 180 m2
A2 = 100 m2](https://image.slidesharecdn.com/glaucoexerciciosresolvidos1-160318123632/85/Glauco-exercicios-resolvidos-1-108-320.jpg)