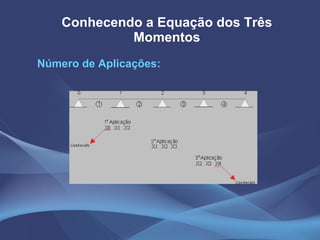
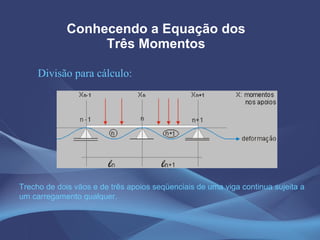
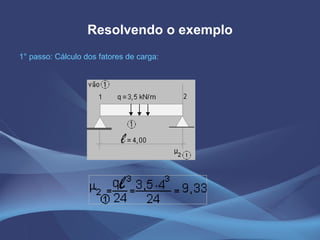
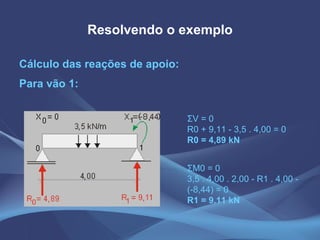
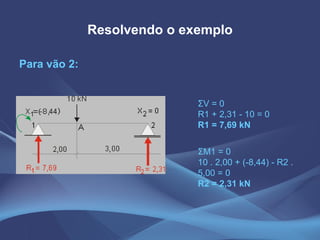
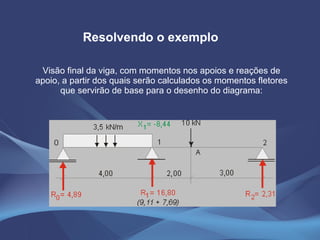
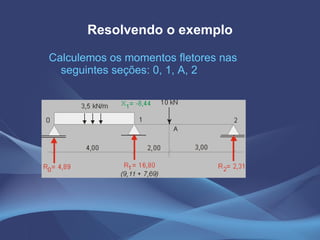
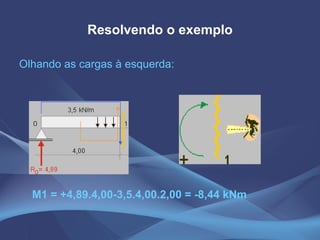
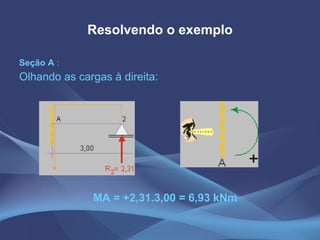
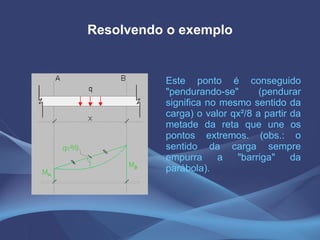
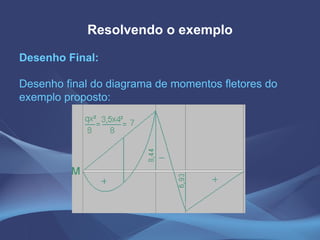
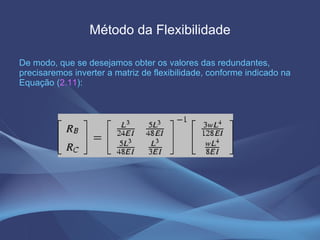
Este documento discute o método da equação dos três momentos e o método da flexibilidade para análise de vigas contínuas. Apresenta exemplos numéricos de cálculo de momentos fletores, reações de apoio e diagramas de esforços usando a equação dos três momentos. Também explica os conceitos teóricos e os passos para aplicação do método da flexibilidade.

1. SEMINÁRIO SOBRE O MÉTODO DA FLEXIBILIDADE E A EQUAÇÃO DOS TRÊS MOMENTOS. Acadêmicas:Fernanda Fernandes Martins Viviane Martins Pelotas, 10 de Novembro de 2008

2. Introdução Vigas Contínuas ou Vigas Hiperestáticas

3. Exemplos de vigas contínuas

4. Conhecendo a Equação dos Três Momentos Quando surgiu? No século XIX. Quem desenvolveu a teoria da Equação dos Três Momentos? Os engenheiros franceses Clapeyron e Bertolt.

5. Conhecendo a Equação dos Três Momentos O que é a equação dos três momentos? É uma equação que relaciona três momentos fletores concentrados na viga de dois em dois vãos. E assim teremos tantas equações quantos os momentos fletores desconhecidos na viga.

6. Conhecendo a Equação dos Três Momentos Número de Aplicações:

7. Conhecendo a Equação dos Três Momentos Trecho de dois vãos e de três apoios seqüenciais de uma viga continua sujeita a um carregamento qualquer. Divisão para cálculo:

8. Conhecendo a Equação dos Três Momentos O’b= Ma.La + Mb.La + Aa.Xa 6.EIa 3.EIa EIa.La O”b= Mb.Lb + Mc.Lb + Ab.Xb 3EIb 6EIb EIb.Lb Fórmulas citadas no livro Mecânica dos Sólidos por Timoshenko/Gere. O’b=- O”b Pois as inclinações da viga biapoiada devem concordar uma com a outra em “b” . Expressão mais geral para equação dos três momentos: Ma (La/Ia) + 2Mb (La/Ia)+(Lb/Ib) + Mc (Lb/Ib)

9. e :comprimento dos vãos Xn-1, Xn e Xn+1: momentos nos apoios : Fatores de carga Onde: Outras fórmulas para Equação dos três momentos : n+1=2 n=1 Vãos n+1=2 n=1 n-1=0 Apoios

10. Cálculo do fator de carga ( µ n ) Para carga uniformemente distribuída ao longo do vão:

11. Cálculo do fator de carga ( µ n ) Para carga concentrada no vão:

12. Exemplo Viga contínua de três apoios e dois vãos.

13. Resolvendo o exemplo 1° passo: Cálculo dos fatores de carga:

14. Resolvendo o exemplo 1° passo: Cálculo dos fatores de carga:

15. Resolvendo o exemplo Resolvendo a 1ª aplicação: 2(4,00 + 5,00).X1 = -6(9,33 + 16,00) X1 = - 8,44 kNm

16. Resolvendo o exemplo Cálculo das reações de apoio: Para vão 1: Σ V = 0 R0 + 9,11 - 3,5 . 4,00 = 0 R0 = 4,89 kN Σ M0 = 0 3,5 . 4,00 . 2,00 - R1 . 4,00 - (-8,44) = 0 R1 = 9.11 kN

17. Resolvendo o exemplo Para vão 2: Σ V = 0 R1 + 2,31 - 10 = 0 R1 = 7,69 kN Σ M1 = 0 10 . 2,00 + (-8,44) - R2 . 5,00 = 0 R2 = 2,31 kN

18. Visão final da viga, com momentos nos apoios e reações de apoio, a partir dos quais serão calculados os momentos fletores que servirão de base para o desenho do diagrama: Resolvendo o exemplo

19. Resolvendo o exemplo Cálculo dos Momentos Fletores: Observações: Momentos fletores: nas seções de início e de fim de carga distribuída e nas seções de carga concentrada. As reações de apoio são cargas concentradas. É indiferente olhar as cargas à esquerda ou à direita de uma determinada seção, o resultado é sempre o mesmo.

20. Resolvendo o exemplo Calculemos os momentos fletores nas seguintes seções: 0, 1, A, 2

21. Resolvendo o exemplo Seção 0 M0 = X0 = 0 Seção 1 M1 = X1 = - 8,44 kNm Analise das Seções:

22. Resolvendo o exemplo Olhando as cargas à esquerda: M1 = +4,89.4,00-3,5.4,00.2,00 = -8,44 kNm

23. Seção A : Olhando as cargas à direita: Resolvendo o exemplo MA = +2,31.3,00 = 6,93 kNm

24. Desenho dos Diagramas: Resolvendo o exemplo Algumas convenções devem ser seguidas: valores de momento fletor positivos, abaixo da linha de referência e negativos, acima desta linha. linha do diagrama de momentos fletores entre dois pontos consecutivos. se não houver carga entre estes dois pontos, a linha é reta e inclinada. se houver carga distribuída entre estes dois pontos, a linha é uma parábola do 2° grau.

25. Resolvendo o exemplo Este ponto é conseguido "pendurando-se" (pendurar significa no mesmo sentido da carga) o valor qx²/8 a partir da metade da reta que une os pontos extremos. (obs.: o sentido da carga sempre empurra a "barriga" da parábola).

26. Resolvendo o exemplo Desenho Final: Desenho final do diagrama de momentos fletores do exemplo proposto:

27. Fixando o Método Observação: O ponto sob o qual se "pendura" o valor qx2/8 não é necessariamente o ponto de máximo momento fletor. Cálculo dos fatores de carga (Fórmula) Cálculo dos momento dos apoios (Fórmula) Cálculo da Reações de Apoio (Somatórios) Cálculo dos Momentos Fletores (Seções) Diagrama Final Roteiro:

28. Método da Flexibilidade Os fundamentos teóricos do método da flexibilidade, podem ser utilizado na solução de qualquer método estaticamente indeterminado, ou seja, toda vez que existirem mais forças incógnitas do que equações de equilíbrio disponíveis para a solução do problema. No método da flexibilidade as incógnitas a serem calculadas são as redundantes estáticas, significando que o número de íncógnitas a calcular é igual ao grau de indeterminação estática (GE). GE=n° de reações nos apoios + n° de barras . N° de esforços – n° de nós . N° de equações

29. Método da Flexibilidade Quando a análise é realizada pelo método da flexibilidade, logo após identificar os redundantes estáticos, procedi-se a "liberação das restrições onde se encontravam tais redundantes”. No método da flexibilidade, logo após a "liberação da estrutura aplicava-se consecutivamente os carregamentos reais e os redundates a fim de se obterem os deslocamentos de cada uma dessas duas situações (viga liberada sujeita aos carregamentos e viga liberada sujeita aos redundates) provocadas nos nós analizados. Este método se utiliza das equações matriciais e estas necessitam que as cargas da estrutura estejam atuando unicamente nos nós, porém geralmente as cargas reais de uma estrutura não cumprem este requisito. As cargas podem ser dividas em dois tipos cargas nodais e caragas que atuam nos membros e estas devem ser substituídas por cargas estaticamente equivalentes que atuem nos nós, estas cargas são chamadas de cargas nodais equivalentes. Quando estas cargas são adicionadas as cargas reais dos nós a carga total é denominada carga nodal combinada. E depois disso a estrutura pode ser analisada pelos métodos matriciais

30. Abordagem Matricial Agora vejamos o caso apresentado na Figura 18 :

31. Método da Flexibilidade No caso da viga apresentada na Figura 18 -(a) temos uma estrutura estaticamente indeterminada do segundo grau, e neste caso, a solução do problema via método da flexibilidade requer que sejam rompidos dois vínculos da viga. No caso específico da viga da Figura 18 -(a) foram rompidos os vínculos dos apoios B e C. Como determina o método da flexibilidade, foram colocados os redundantes estáticos e no locais onde os vínculos foram rompidos, resultando no esquema estrutural da Figura 18 -(c). O próximo passo é calcular os deslocamentos na estrutura liberada nos pontos onde atuam os redundantes. Em primeiro lugar, calculam-se os deslocamentos devido a ação do carregamento que solicita a estrutura (o carregamento distribuído ). Em seguida calculam-se os deslocamentos devido a ação dos redundates e . A partir de agora, chamaremos os deslocamentos devido aos carregamento de . O subíndice indica apenas que é um deslocamento devido ao carregamento (em inglês load ), não sendo propriamente um subíndice, mais um indicador. Os terão os subíndeces , que indicam a posição onde o deslocamento está sendo calculado. Para o caso apresentado na Figura 18 -(d), podemos calcular e através da técnica da carga virtual unitária do modo ilustrado nas Figuras 19 e 20 .

32. Método da Flexibilidade

33. Método da Flexibilidade

34. Método da Flexibilidade

35. Método da Flexibilidade

36. Método da Flexibilidade Agora que já sabemos as flexibilidades nos pontos 1 e 2, podemos calcular os deslocamentos na estrutura liberada devido a ação das redundantes estáticas. Uma vez que já foram calculadas as flexibilidades, podemos expressar os deslocamentos na forma da Equação ( 2.5 ):

37. Adotando a nomeclatura semelhante a utilizada por gereweaver, nominaremos os deslocamentos gerais como ; os deslocamentos devido as cargas de , e as forças redundates denotadas por . Desse modo a Equação ( 2.7 ), é reescrita em temos gerais na forma da Equação ( 2.8 ):

38. Método da Flexibilidade Substituindo os valores já calculados para a Equação ( 2.8 ), obteremos a Equação ( 2.9 ):

39. Método da Flexibilidade Agora, se desejamos obter os valores das redundantes , isolamos esse termo da Equação ( 2.9 ), obtendo a Equação ( 2.10 ):

40. Método da Flexibilidade De modo, que se desejamos obter os valores das redundantes, precisaremos inverter a matriz de flexibilidade, conforme indicado na Equação ( 2.11 ):

41. Método da Flexibilidade Utilizando a técnica algébrica descrita em boldrini, podemos obter a inversa da matriz de flexibilidade, dada pela Equação ( 2.12 ):

42. Método da Flexibilidade Assim, podemos reescrever a Equação ( 2.11 ) na forma da Equação ( 2.13 ):

43. Método da Flexibilidade Resolvendo ( 2.13 ), chegamos aos valores dos redundantes expressos na Equação ( 2.14 )

44. Roteiro para Método da Flexibilidade Caracterização do problema Cálculo do grau de indeterminação estática Identificar possíveis redundantes estáticas Escolha da estrutura liberada Cálculo de deslocamentos na estrutura liberada devido a ação dos carregamentos reais Cálculo de deslocamentos na estrutura liberada devido a ação dos redundantes estáticos Montagem da equação de compatibilidade Solução da equação de compatibilidade Cálculo de demais deslocamentos, reações, etc Obtençaõ dos hiperestáticos Obtenção dos efeitos finais (eq. efeitos finais)

45. Semelhanças entre os métodos Ambos analisam vigas contínuas e estruturas hiperestáticas. Ambos analisam a estrutura por partes (flex vão a vão e 3 momentos 2 vãos em 2 vãos). Em ambas se faz o somatório das reações verticais e dos momentos. Σ v=0 e Σ M=0 Em ambos o objetivo é traçar o diagrama final de esforços da estrutura. Ambos utilizam nos cálculos a constante EI. ...

46. Diferenças entre os métodos Método da Equação dos três momentos - utiliza momentos de inécia e áreas da estrutura. Método da Flexibilidade - utiliza matrizes. Método da Flexibilidade - utiliza somente cargas nodais ou cargas nodais equivalentes. Método da Equação dos três momentos - utiliza as cargas reais da estrutura. Método da Flexibilidade - o 1° passo é calcular o GE. Método da Equação dos três momentos - Não utiliza GE, o 1° passo é calcular os fatores de cargas.

47. Diferenças entre os métodos Método Flexibilidade - escolha estrutura liberada. Método Flexibilidade - Se tem redundantes estáticas. Método Flexibilidade - se analisa a estrutura vão a vão. Método da equação dos 3 Momentos - se analisa a estrutura de dois em dois vãos. Método da equação dos 3 Momentos - se soma as reações do mesmo apoio. ...

48. Referencias Bibliográficas Mecânica dos sólidos;Livros tecnicos e cientificos editora 1981; S. P. Timoshenko e J. E. Gere. Resistência dos materiais; editora Universidade de São Paulo em 1966, Timoshenko, Stephen P. http://www.engenhariacivil.ueg.br/ http://www.lami.pucpr.br/ Material de Estrutura de Analise II, Cristiane, 2008