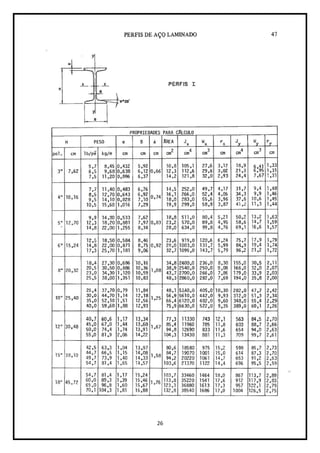
Este documento fornece exemplos de exercícios sobre resistência dos materiais, incluindo cálculos de tensões, alongamentos e determinação de áreas de seção transversal de barras sob cargas axiais. Resolve exemplos como determinar tensões em diferentes trechos de uma barra sob múltiplas forças, calcular alongamentos em barras elásticas e dimensionar perfis estruturais.

1. 1
COMPLEMENTO DE
RESISTÊNCIA DOS MATERIAIS
CARLOS WALTER VICENTINI
LISTA DE EXERCÍCIOS 1 Tensões
NOTAS DE AULAS MINISTRADAS PARA A TURMA DE ENGENHARIA
CIVIL (5º/6º CICLO) DA UNIP
Santos, agosto de 2013

2. 2
1. Determinar o alongamento e a tensão normal atuante em uma barra
prismática (figura abaixo) com 850 mm de comprimento, seção transversal
retangular de 10 mm x 20 mm e com módulo de elasticidade E = 200 GPa. F
= 20 kN
Solução
(0,010 x 0,020) = 100000000 N/m² = 100 Mpa
Supondo que está na região elástica e, portanto, obedecendo a lei de Hooke,
3
-­4
mm/mm
0 0 = 5*10-­4
* 850
Resposta
2. A barra de aço da figura abaixo tem seção transversal A = 10 cm² e está
solicitada pelas forças axiais representadas. Determinar o alongamento da
barra e as tensões que atuam nos diversos trechos, sabendo-­se que E =
2100 tf/cm².
Solução
Trecho AB:
10000 = 0 portanto N = 10000 kgf
AB = N/A = 10000 kgf / 10 = 1000 kgf/cm²
e = 2500 kgf/cm² e podemos dizer que a tensão que atua
no trecho AB é inferior a esse valor, logo está na região elástica e segue a lei de
= 1000 kgf/cm² / 2100000 kgf/cm² = 4,76*10-­4
cm/cm

3. 3
0 0 = 4,76*10-­4
* 2000 mm
AB = 0,95 mm Resposta
Trecho BC:
10000 + 3000 = 0 portanto N = 7000 kgf
BC = N/A = 7000 kgf / 10 = 700 kgf/cm²
= 700 kgf/cm² / 2100000 kgf/cm² =
3,33*10-­4
cm/cm
0 0 = 3,33*10-­4
* 3000 mm
BC = 1 mm Resposta
Trecho CD:
-­ N = 0 portanto N = 9000 kgf
CD = N/A = 9000 kgf / 10 = 900 kgf/cm²
= 900 kgf/cm² / 2100000 kgf/cm² =
4,29*10-­4
cm/cm
0 0 = 4,29*10-­4
* 4000 mm
CD = 1,72 mm Resposta
3. A treliça Howe da figura suporta a força de 54 t. Determinar as áreas das
seções transversais das barras DE e AC, sabendo-­se que a tensão admissível
do material, a tração, é de 1400 kgf/cm². Sendo de 2 m o comprimento da
barra DE, pergunta-­se qual o seu alongamento, admitindo para o módulo de
elasticidade do material o valor de E = 2,1 x 106
kgf/cm².
Após a determinação das áreas, escolha o perfil mais adequado da tabela dada
no final da lista de exercícios.

4. 4
4. Duas barras iguais, de aço, são articuladas nas extremidades e suportam
uma carga de 45 tf, tal como indicado na figura. Adotando-­se a tensão
admissível de 2100 kgf/cm², pede-­se determinar a área da seção transversal
dessas barras e o deslocamento vertical do nó B. São dados: E = 2,1 x 106
kgf/cm² e o comprimento da barra l = 3 m.
Solução:

5. 5
TAB cos45° + TBC cos45° -­ 45 tf = 0
TAB cos45° + TBC cos45° = 45 tf 0,707(TAB + TBC) = 45
TAB + TBC = 63,64 tf
Fx = 0: TBC cos45° -­ TAB cos45° = 0;; portanto TBC = TAB
Logo, TBC = TAB = 63,64/2 = 31,82 tf
adm = 2100 kgf/cm² = N/A;; portanto A = N/21000 = 31820/2100
A = 15,15 cm² Resposta
, portanto:
AB BC
AB BC/0,707
AB/l0 AB AB/E = N/AE AB = 31820 kgf/(15,15cm² * 2,1E6 kgf/cm²)
AB = 0,001 AB AB * l0 = 0,001*3000 mm
AB = 3 mm
Resposta
5. Considere o pino de 12 mm de diâmetro da ligação da figura. Sendo a força
P = 9000 N, determine o valor da tensão média de cisalhamento que atua na
seção transversal a-­a do pino considerando que sua distribuição seja
uniforme. Determine também as tensões de esmagamento que ocorrem nas
c d
Solução:
Cisalhamento duplo:
Fx = 0: V + V P = 0 2V = P V = P/2
²/4)
Resposta
Esmagamento na chapa central -­ d = 20 mm:
es = P/Aproj = 9000 N / (0,012*0,020) es = 37,5 Mpa Resposta

6. 6
Esmagamento nas chapas superior e inferior -­ c = 15 mm:
es = P/2Aproj = 9000 N /2 (0,012*0,015) es = 25,0 Mpa Resposta
6. De acordo com a figura, a força P tende a fazer com que a peça superior
deslize em relação à inferior segundo o plano a-­a. Sendo P = 4000 kgf, qual
a tensão de cisalhamento nesse plano?
Solução:
A força de cisalhamento que atua no plano a-­a é provocada pela componente
horizontal de P. Logo temos:
Px = P cos45° = 4000*0,707 Px = 2828 kgf
A área em que atua a força Px vale: A = 20*30 = 600 cm²
Logo a tensão de cisalhamento será:
= Px/A = 2828/600 Resposta
7. Considere o corpo de prova da figura, de seção transversal retangular de 2,5
cm por 5,0 cm, utilizado para determinar a resistência à tração da madeira.
Sendo para a peroba a tensão de ruptura ao cisalhamento de 130 kgf/cm²,
pede-­ a
a ruptura se dê por tração e não por cisalhamento. A carga de ruptura à
tração é P = 1040 kgf.
Solução:
Se a carga de ruptura a tração é P = 1040 kgf, isso significa que com essa
carga eu não posso ter ruptura por cisalhamento. Então, como eu terei
P/2A rup então,
a 0,8 cm Resposta

7. 7
8. Uma viga de madeira, com seção retangular com b=10cm e h=18cm tem 6m
de vão e a tensão admissível é 9Mpa. Calcular a máxima carga P que pode
ser aplicada no meio do vão.
Solução:
W = bh²/6 = 0,10*0,18²/6 = 0,00054 m³
O momento máximo ocorre no ponto de aplicação da carga (centro do vão) e
vale: Mmax = PL/4 = P*6/4 = 1,5P
9E6 N/m² = 1,5P Nm / 0,00054 m³
P = 9E6*0,00054/1,5 P = 3240 N Resposta
9. Calcular o valor da tensão máxima devido à flexão na viga prismática de
concreto armado da figura. Represente a distribuição das tensões na seção
transversal da viga.
São dados: c=2,5tf/m³;; alv=2,0tf/m³;; e=0,8m.
Solução:
Cálculo da carga distribuída devido ao peso próprio do concreto:
qcon c * 1 * 1 = 2,5 tf/m
Cálculo da carga distribuída devido ao peso próprio da parede de alvenaria:
qalv alv * 8 * 0,8 = 12,8 tf/m
q = qcon + qalv = 15,3 tf/m
O momento máximo vale: Mmax = ql²/8 = 15,3*12²/8 = 275,4 tfm
O módulo de resistência à flexão, W, será:
W = bh²/6 = 1*1²/6 = 0,17 m³
A tensão normal máxima devido à flexão será:

8. 8
max = Mmax/W = 275,4/0,17
max = 1620 tf/m² ou max = 162 kgf/cm² Resposta
10. A viga de concreto armado da figura suporta duas colunas iguais de
concreto, com 30cm de diâmetro e tensão de compressão de 120kgf/cm² na
base, sendo a sua seção transversal retangular com 60cm de base e 90cm
de altura, com peso específico c=2,5tf/m³. Determine o valor da tensão
máxima de compressão na viga e represente a distribuição das tensões na
seção.
Solução:
Cálculo da carga distribuída devido ao peso próprio do concreto:
qcon c * 0,6 * 0,9 = 1,35 tf/m
Cálculo da carga concentrada P devido à coluna de concreto:
Acol = d²/4 = *0,3²/4 = 0,071 m²
P = *A = 120*0,071*100² = 85200 kgf = 85,2 tf
Mmax = ql²/8 + VA*2 = 1,35*10²/8 + 85,2*2 = 187,275 tfm
O módulo de resistência à flexão, W, será:
W = bh²/6 = 0,6*0,9²/6 = 0,081 m³
A tensão normal máxima devido à flexão será:
max = Mmax/W = 187,3/0,081
max = 2312 tf/m² ou max = 231,2 kgf/cm² Resposta

9. 9
11.Determine para a viga representada na figura abaixo, os diagramas de força
cortante, momento fletor.
Após a obtenção dos diagramas, faça com que w0 = 2 kN/m, L = 3m, calcule a
tensão de flexão máxima absoluta e represente a distribuição de tensão na
seção transversal da viga.
Considere uma viga em perfil I 203,2 x 27,3 dada na tabela de perfis que se
encontra no final da lista de exercícios.
Solução:
Reações de apoio. A carga distribuída é substituída por sua resultante e as reações
são determinadas com as equações de equilíbrio como segue
y = 0;; RA w0 L/2 = 0 ou RA = w0 L/2
A = 0;; MA (w0 L/2) (2L/3) = 0 ou MA = w0 L²/3
Funções de cisalhamento e momento fletor. Um diagrama de corpo livre de um
segmento com comprimento x é desenhado na figura (c). A intensidade da carga é
determinada por semelhança de triângulos, ou seja, w/x = w0/L e, portanto, w =
w0x/L.

10. 10
y = 0;; w0 L/2 (½)(w0 x/L)x V = 0 ou V = w0/2L (L² -­ x²) (1)
x = 0;; (w0 L²/3) -­ w0 L/2 (x) + (½)(w0 x/L)x (x -­ 2x/3) + M = 0 ou M =
w0/6L (-­2L³ + 3L²x x³) (2)

11. 11
Diagramas de força cortante e momento fletor. Os gráficos das equações (1) e
(2) estão mostrados na figura (d).
Fazendo-­se w0 = 2 kN/m e L = 3m, obtemos os valores de V e M que são
V = w0 L/2 = (2 kN/m) (3 m)/2 = 3 kN
M = -­ (w0 L²)/3 = (2 kN/m) (3 m)² / 3 = -­6 kNm
Nota: O valor negativo do momento significa que as fibras inferiores são comprimidas
e as superiores tracionadas.
Consultando a tabela da página 5, I 203,2 x 27,3, obtemos os valores de Ix = 2400
cm4
;; h = 20,32 cm;; Wx = 236 cm³.
portanto, Ix = 2400 (1/1004
) m4
;; h = 20,32 (1/100) m ;; Wx = 236 (1/100³) m³.
Logo, Ix = 2,4 10-­5
m4
;; h = 2,032 10-­1
m;; Wx = 2,36 10-­4
m³.

12. 12
c = h/2 = (2,032 10-­1
)/2 = 1,016 10-­1
m
como máx = M c/I, temos que máx = (-­6 kNm) (1,016 10-­1
m)/ 2,4 10-­5
m4
, então
máx = -­2,54 104
N/m² = -­2,54 104
Pa = -­25,4 kPa Resposta
Nota:
Podemos usar também a seguinte equação: máx = M / W e então teremos: máx =
(-­6 kNm)/(2,36 10-­4
m³) = 25423,7 N/m² ou aproximadamente 25,4 kPa.
12. Determine para a viga com um balanço representada na figura abaixo, os
diagramas de força cortante, momento fletor.
Após a obtenção dos diagramas, faça com que p = 15 kN/m, L = 4 m, a = 3 m
e b = 1 m. Calcule a tensão de flexão máxima absoluta e represente a
distribuição de tensão na seção transversal da viga.
Escolha o perfil mais econômico, portanto mais adequado, consultando a tabela
a seguir e considerando que o material da viga apresenta uma tensão
admissível Adm = 150 MPa .

13. 13
Solução
Reações de apoio. A carga distribuída é substituída por sua resultante e as reações
são determinadas com as equações de equilíbrio como segue
y = 0;; RA + RB p L = 0 ou RA = p L -­ RB
A = 0;; RB a -­ p L L/2 = 0 ou RB = p L²/2 a
então RA = p L p L²/2 a = p L (1 L/2a)
Funções de cisalhamento e momento fletor. Um diagrama de corpo livre de um
segmento no trecho AB com comprimento x é desenhado na figura (c).
y = 0;; RA p x -­ V= 0 ou V = p L (1 L/2a) p x
para x = 0 temos V = p L (1 L/2a)
para x = a temos V = p L (1 L/2a) p a

14. 14
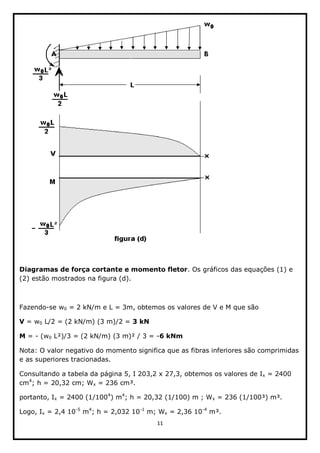
Onde V(x) = 0 o momento será máximo, logo para sabermos onde V(x) corta o eixo
dos x, igualamos V(x) a zero.
V = p L (1 L/2a) p x = 0 então x = [p L (1 L/2a)]/p
x = L (1 L/2a)
x = 0;; M RA x + p x (x/2) = 0 ou
M = p L (1 L/2a) x -­ p x²/2
para x = 0 temos M = 0
para x = a temos M = p L (a L/2) -­ p a²/2
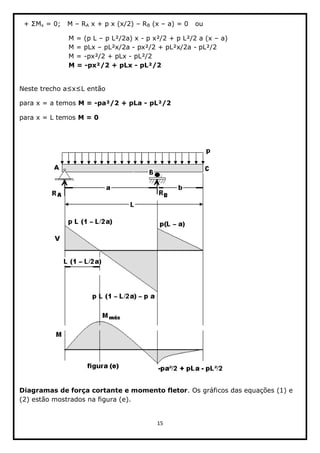
Um diagrama de corpo livre de um segmento no trecho BC com comprimento x é
desenhado na figura (d) e aplicadas as equações de equilíbrio para determinação das
equações dos esforços internos M e V.
y = 0;; RA p x + RB V = 0 ou
V = p L p L²/2a p x + p L²/2 a ou V = pL p x = p(L x)
então
para x = a temos V = p(L a)
para x = L temos V = 0

15. 15
x = 0;; M RA x + p x (x/2) RB (x a) = 0 ou
M = (p L p L²/2a) x -­ p x²/2 + p L²/2 a (x a)
M = pLx pL²x/2a -­ px²/2 + pL²x/2a -­ pL²/2
M = -­px²/2 + pLx -­ pL²/2
M = -­px²/2 + pLx -­ pL²/2
então
para x = a temos M = -­pa²/2 + pLa -­ pL²/2
para x = L temos M = 0
Diagramas de força cortante e momento fletor. Os gráficos das equações (1) e
(2) estão mostrados na figura (e).

16. 16
Fazendo-­se p = 15 kN/m, L = 4 m, a = 3 m e b = 1 m, como pedido no enunciado do
exercício, temos, no trecho AB, pois é lá que encontramos Mmáx substituindo x por L(1
L/2a) = 4 m [1 (4 m)/(2 3 m) = 1,33 m.
A equação do momento para o trecho AB é dada pela expressão:
M = p L (1 L/2a) x -­ p x²/2. Substituindo os valores teremos:
M = (15 kN/m)(4 m)[1 (4 m)/(2 3 m)] (1,33 m) (15 kN/m) (1,33 m)² /2 = 13,3
kNm.
Adm podemos dizer que
Adm
Então, se igualarmos as expressões acima obtemos:
Adm Adm
Logo, W = (13,3 kNm)/(150 MPa) = 8,9 10-­5
m3
= 89 cm³
Para a escolha do perfil mais econômico, portanto mais adequado, consultando
a tabela da página 5, encontramos uma viga I 127 x 18,2 cujo valor de Wx =
89,8 cm3
Resposta
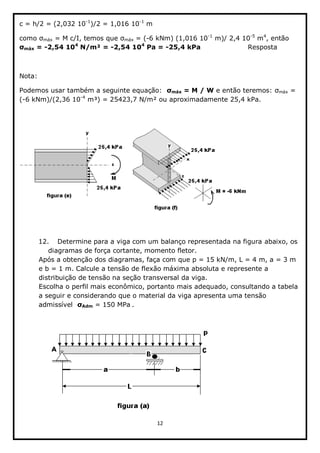
Então a tensão máxima de flexão vale:
máx = M/W = (13,3 kNm)/(89,8 cm³)
máx = (13,3 kNm)/(8,98 10-­5
m³)
máx = 148,1 MPa Resposta
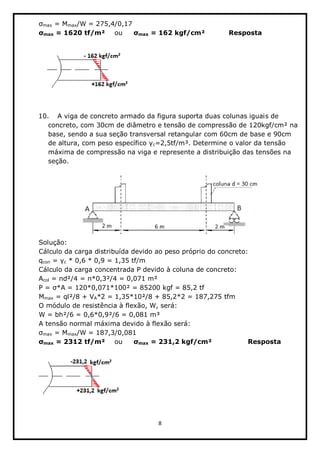
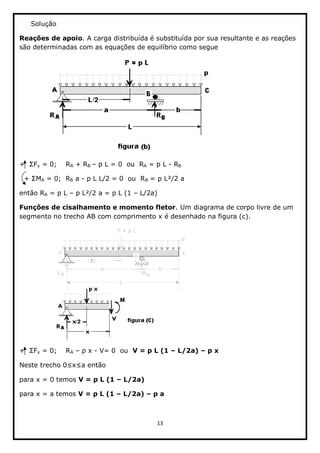
13. A peça de mármore, que podemos considerar como um material linear elástico
frágil, tem peso específico de 24 kN/m³ e espessura de 20 mm. Calcule a tensão
de flexão máxima da peça se ela estiver apoiada (a) em seu lado e (b) em suas
Rup = 1,5 MPa, explique as consequências de
apoiar a peça em cada uma das posições.
Solução: Esquema estático adotado:

17. 17
Como já vimos anteriormente, o valor de momento máximo para esse esquema
estático é:
M = w L²/8
Portanto temos que determinar o valor de w que é:
mármore Vpeça / L= (24 kN/m³) (1,5 m x 0,5 m x 0,02 m)/1,5 m
w = 240 N/m e L = 1,5 m
então,
M = 240 N/m (1,5 m)²/8 = 67,5 Nm
Cálculo do momento de inércia da peça:
1. Para a posição (a) temos:
Ix = b h³/12 = 0,02 m (0,5 m)³/12 = 2,08 10-­4
m4
Wx = Ix/c = Ix 2/h = 8,33 10-­4
m³
então máx = M/W = 67,5 Nm / 8,33 10-­4
m³ = 0,081 MPa Rup
2. Para a posição (b) temos:
Ix = b h³/12 = 0,5 m (0,02 m)³/12 = 3,33 10-­7
m4

18. 18
Wx = Ix/c = Ix 2/h = 3,33 10-­5
m³
então máx = M/W = 67,5 Nm / 3,33 10-­5
m³ = 2,025 MPa Rup
Portanto na posição (a) a peça resiste mas na posição (b) a peça se
rompe. Resposta
14. Uma viga composta é feita de madeira e reforçada com uma tira de aço
localizada em sua parte inferior. Ela tem a área de seção transversal
mostrada na figura. Se for submetida a um momento fletor M = 2 kNm,
determine a tensão normal nos pontos B e C. Considere Eaço = 200 GPa. Emad
= 12 GPa.
Solução
Solução
Propriedades da seção. Embora a escolha seja arbitrária, aqui, transformaremos a
seção em outra feita inteiramente de aço. Visto que o aço tem rigidez maior que a da
madeira (Eaço > Emad), a largura da madeira deve ser reduzida a uma largura
equivalente para o aço. Por conseqüência n deve ser menor do que um. Para tanto, n
= Emad/ Eaço, então
baço = nbmad = [(12 GPa)/(200GPa)](150 mm) = 9 mm
A seção transformada é mostrada na figura 86b.

19. 19
A localização do centróide (eixo neutro), calculada em relação a um eixo de referência
localizado na parte inferior da seção, é
y = [(0,01 m)(0,02 m)(0,15 m) + (0,095 m)(0,009 m)(0,15 m)]/
/[0,02 m(0,15 m) + 0,009 m (0,15 m)] = 0,03638 m
Portanto, o momento de inércia em relação ao eixo neutro é
INA=[(1/12)(0,15 m)(0,02 m)³ + (0,15 m)(0,02 m)(0,03638 m 0,01 m)²]
+[(1/12)(0,009 m)(0,15 m)³ + (0,009 m)(0,15 m)(0,095 m 0,03638 m)²]
INA = 9,358(10-­6
) m4
Tensão normal
= Mc/I = 2 kNm (0,170 m 0,03638 m)/9,358(10-­6
) m4
= 28,6 MPa
C = 2 kNm (0,03638 m)/9,358(10-­6
) m4
= 7,78 MPa Resposta
A distribuição da tensão normal na seção transformada (toda de aço) é mostrada na
figura 86c.
A tensão normal na madeira, localizada em B na figura 86a, é determinada pela
equação:
B = (12 GPa/200 GPa)(28,56 MPa) = 1,71 MPa Resposta

20. 20
Usando esses conceitos, mostre que a tensão no aço e na madeira no ponto onde elas
aço mad = 0,21 MPa, respectivamente.
A distribuição de tensão normal na viga verdadeira é mostrada na fig. 86d.
15. A viga de concreto armado é feita com duas hastes de reforço de aço. Se a
aço)adm = 280 MPa e a tensão de
compressão admissível para o concreto conc)adm = 21 MPa, determine o
momento máximo M que pode ser aplicado à seção. Considere que o
concreto não pode suportar uma tensão de tração. Eaço =200 GPa, Econc =
26,5 GPa.
Solução
Dados: bf = 550 mm;; df = 100 mm;; bw = 150 mm;; dw = 450 mm
dr = 25 mm hr = 50 mm Econc = 26,5 GPa
Eaço = 200 GPa;; aço)adm conc)adm = 21 MPa
Propriedades da seção

21. 21
n = Eaço/Econc = 200 GPa/26,5 GPa = 7,54717
aço r
-­ aço(dw -­ hr f df(0,5 df w
-­7409,42(450 50
2850,24 = 0
de onde ou h´= -­835,54
Portanto o valor mais aceitável é:
Determinação do momento de inércia da seção:
I = Iaço + If + Iw
Iaço aço(dw -­ hr -­ 50 3,41)² = 1165380460 mm4
If = 1/12(bfdf
3
) + bfdf(0,5df
If = 202727878,8 mm4
Iw = 1/12(bw w
Iw = 1982,6 mm4
I = 1165380460 mm4
+ 202727878,8 mm4
+ 1982,6 mm4
I = 1368110321 mm4
A tensão máxima no concreto será dada por: máx = conc)adm = Mconc cconc /I
onde cconc = df
Então o momento máximo permitido no concreto será:
Mconc = ( conc)admI/cconc = 21 MPa (1368110321 mm4
)/103,41 mm = 277,83 kNm
A tensão máxima no aço será dada por: máx = aço)adm =n Maço caço /I
onde caço = dw -­ hr 50 -­ 3,41 = 396,59 mm
O momento máximo permitido no aço será:

22. 22
Maço = aço)admI/n caço = 280 MPa (1368110321 mm4
)/(7,54717)396,59 mm =
127,98 kNm
Portanto o momento máximo permitido será:
Mmáx = 127,98 kNm Resposta
16. Visto que o concreto só pode suportar pouca ou nenhuma tração, esse
problema pode ser evitado se o concreto for protendido com cabos ou hastes.
Considere a viga simplesmente apoiada mostrada na figura, que tem seção
transversal retangular de 450 mm por 300 mm. Se o peso específico do
concreto for 24 kN/m³, determine a tração exigida na haste AB, que se estende
por toda a viga, de modo que nenhuma tensão de tração seja desenvolvida na
seção central a-­a da viga. Despreze o tamanho da haste e qualquer deflexão da
viga.
Solução
Dados: b = 300 mm;; d = 450 mm;;
L = 2,4 m;; = 24 kN/m³
a = d
Cálculo das reações: por simetria, RA = RB = R
y = 0;; 2R wL = 0;; R = wL/2 = 3,888 kN

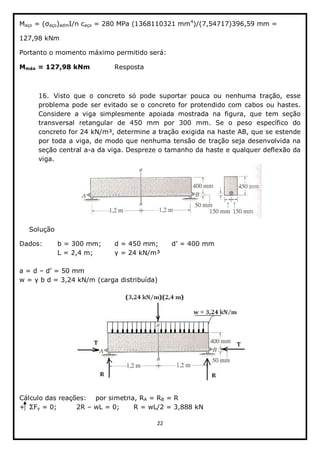
23. 23
Esforços internos (normal e momento fletor):
x = 0;; T N = 0;; N = T
O = 0;; M + T(0,5d a) R(0,5L) + (0,5wL)(0,25L) = 0
M = R(0,25L) T(0,5d a)
Propriedades da seção:
A = bd = 135000 mm²
I = 1/12(b d³) = 2278125000 mm4
Tensão normal: a = N/A + Mc/I
Por imposição do problema: a = 0;; 0 = -­T/A + Mca/I
onde ca = 0,5d
0 = -­T/A + [R(0,25L) T(0,5d a)]ca/I
T = R(0,25L)/ [(0,5d a) + I/(A ca)]
T = 9331 kN Resposta
17. Para reforçar uma viga de aço, uma tábua de carvalho foi colocada entre
seus flanges, como mostra a figura. Se a tensão normal admissível para o aço
adm)aço adm)mad = 21 MPa, determine o
momento fletor máximo que a viga pode suportar com e sem o reforço da
madeira. Eaço = 200 GPa, Emad = 12 GPa. O momento de inércia da viga de aço
é Iz = 7,93 106
mm4
, e sua área de seção transversal é A = 5493,75 mm².
Solução

24. 24
Sem a tábua. Neste caso, o eixo neutro coincide com o eixo z. A aplicação direta da
fórmula da flexão para a viga de aço dá como resultado
adm)aço = Mc/Iz
168 N/mm² = M (105 mm)/7,93 106
mm4
M = 12,688 kNm Resposta
Com a tábua. Visto que agora temos uma viga composta, devemos transformar a
seção em um único material. Será mais fácil transformar a madeira em uma
quantidade equivalente de aço. Para tal, n = Emad/Eaço. Assim, a largura de uma
quantidade equivalente de aço é
baço = nbmad = (12 GPa/200GPa)300 mm = 18 mm
A seção transformada é mostrada na figura.
O eixo neutro encontra-­se em
y = yA/ A = (0)(5493,75 mm²) + (55 mm)(100 mm)(18 mm)/
/[5493,75 mm² + 100(18) mm²] = 13,57 mm
E o momento de inércia em relação ao eixo neutro é
I = [7,93 106
mm4
+ (5493,75 mm²)(13,57 mm)²] +
+ [(1/12)(18 mm)(100 mm)³ + (18 mm)(100 mm)(55 mm 13,57 mm)²]
I = 13,53(106
) mm4
A tensão normal máxima ocorrerá na parte inferior da viga (figura 87b). Aqui, c =
105 mm + 13,57 mm = 118,57 mm. O momento máximo baseado na tensão
admissível para o aço é
adm)aço = Mc/I
168 (106
) N/m² = 168 N/mm² = M(118,57 mm)/13,53(106
) mm4
M = 19,17 kNm
A tensão normal máxima na madeira ocorre na parte superior da viga (figura 87b).
13,5 mad aço, o momento
máximo baseado na tensão admissível para a madeira é

25. 25
adm)mad
6
)mm4
Por comparação, o momento máximo é limitado pela tensão admissível no aço.
Portanto,
M = 19,17 kNm Resposta
Observação: Usando a tábua como reforço, conseguimos 51% de capacidade
adicional para o momento da viga.

26. 26