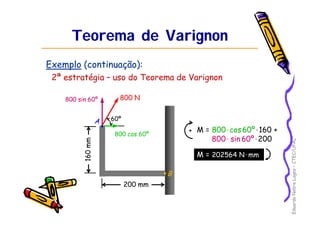
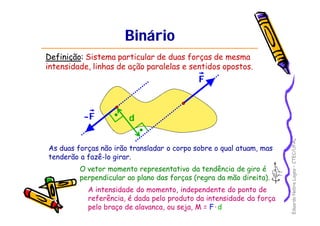
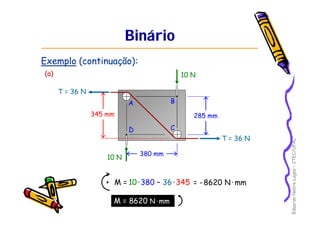
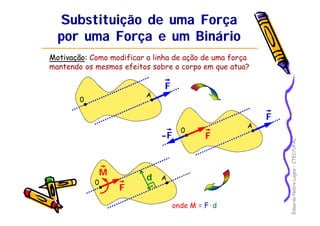
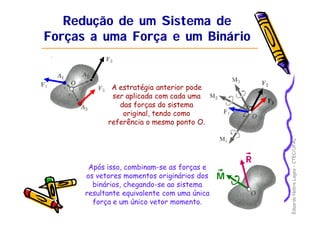
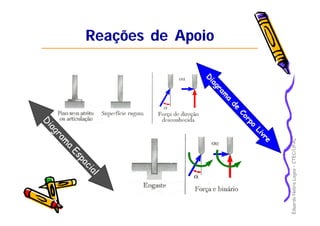
1) O documento discute equilíbrio de corpos rígidos sob a ação de forças, incluindo momentos de forças, binários e redução de sistemas de forças.
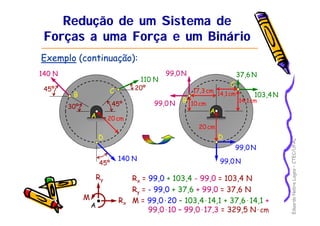
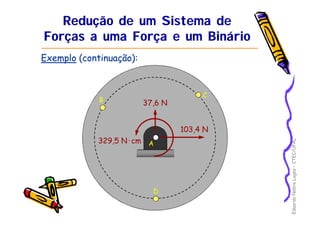
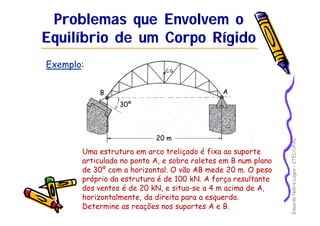
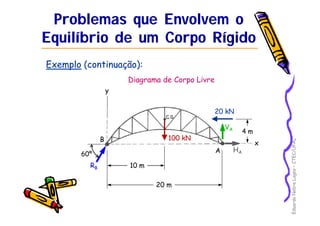
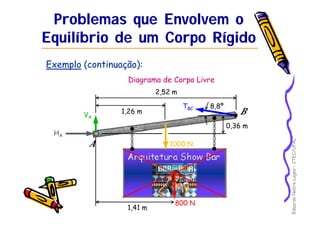
2) É apresentado um exemplo resolvendo as reações em apoios para uma estrutura sob ação de forças.
3) Um segundo exemplo calcula a tração em um cabo e reações em uma articulação para equilibrar um mastro e letreiro.