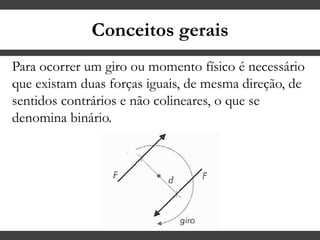
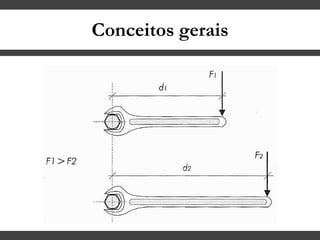
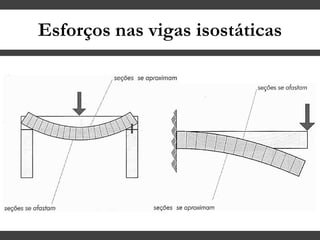
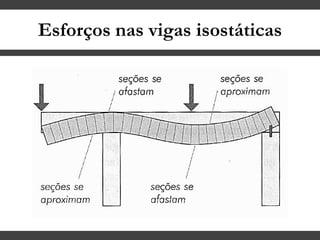
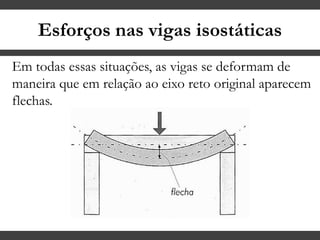
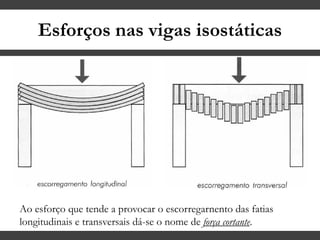
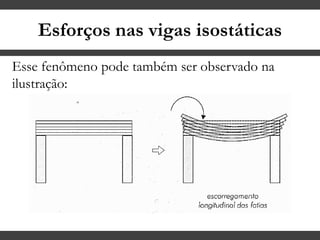
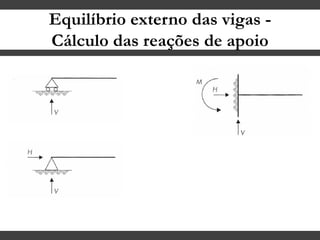
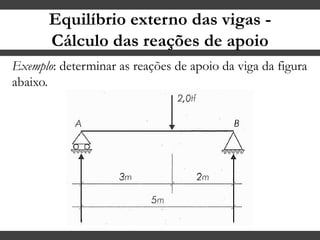
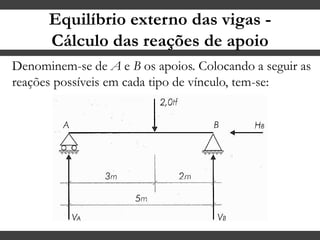
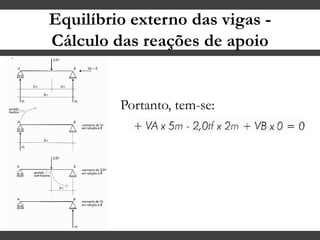
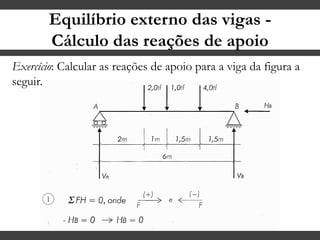
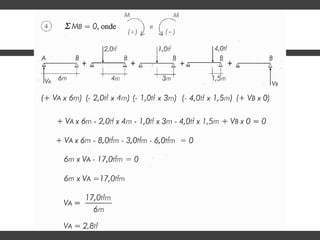
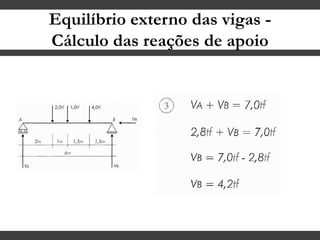
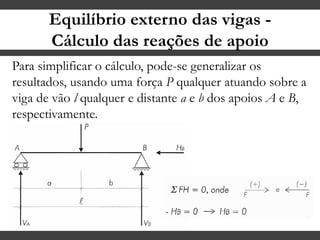
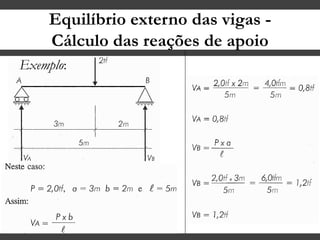
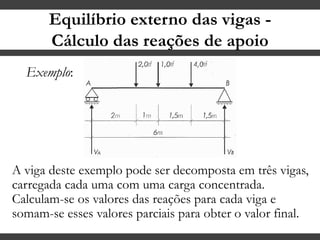
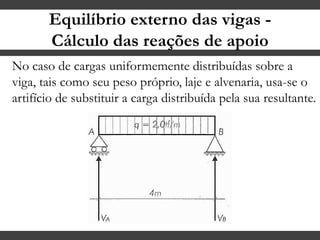
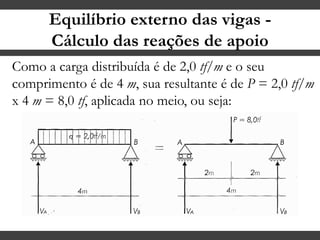
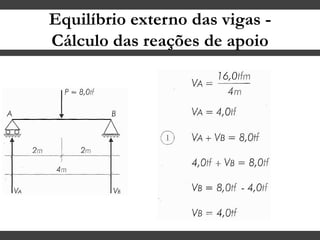
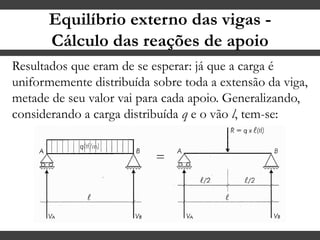
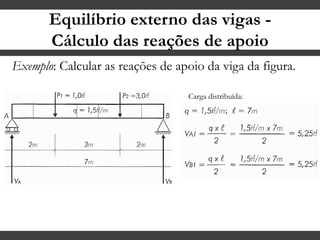
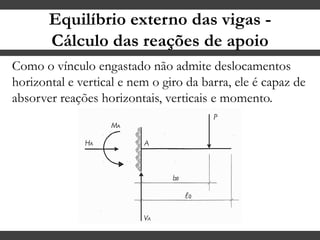
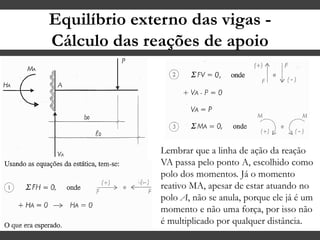
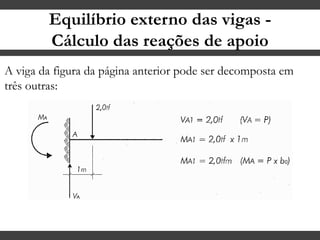
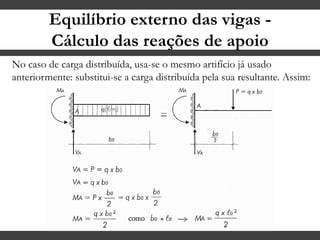
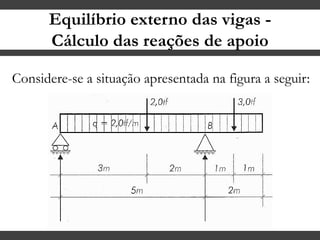
O documento discute conceitos gerais sobre momentos e esforços em vigas, incluindo: (1) a definição de momento como um esforço que provoca giro, (2) os conceitos de binário e distância de força em relação ao ponto de giro, e (3) os tipos de esforços em vigas, como momento fletor e força cortante. O documento também explica como calcular as reações de apoio em vigas isostáticas usando equações de equilíbrio estático.