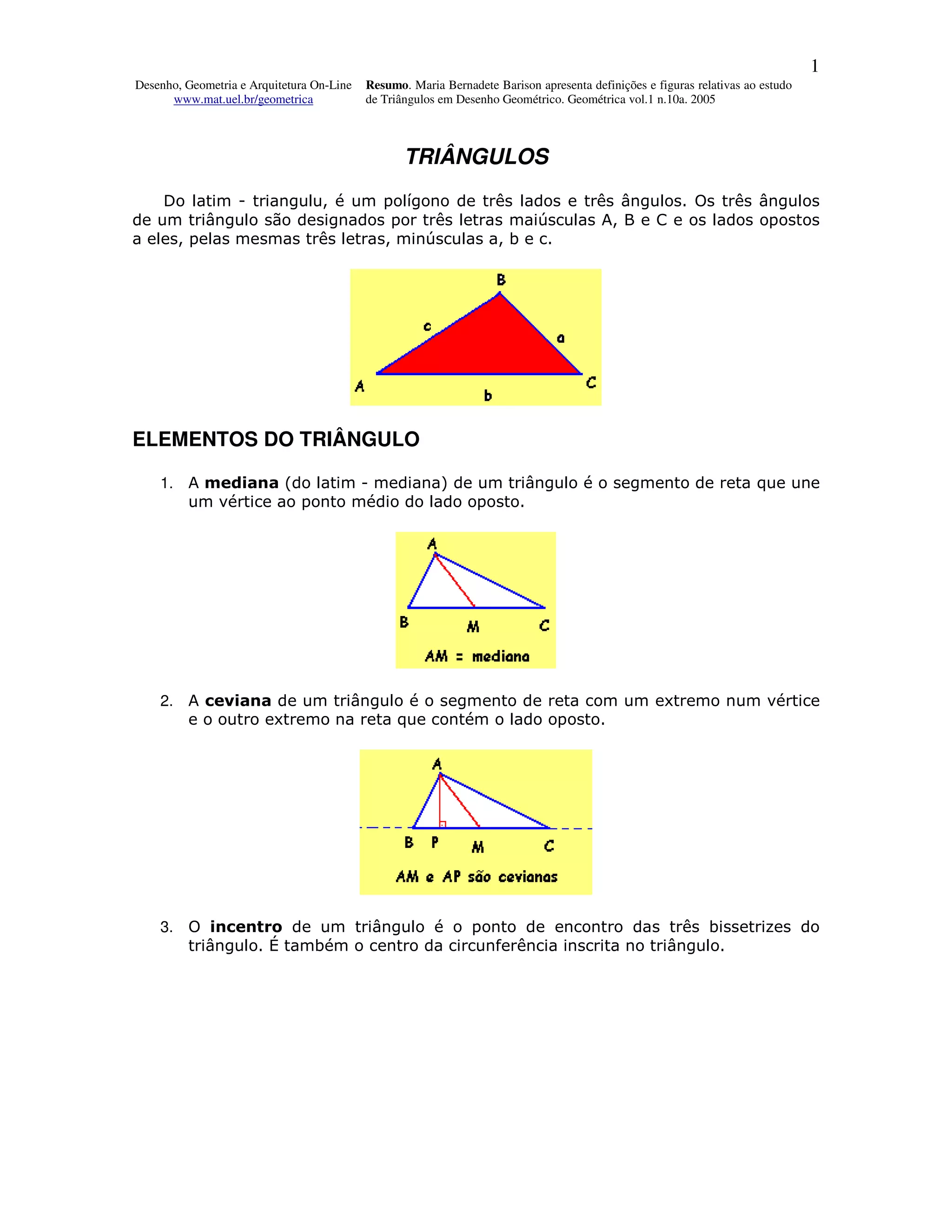
O documento discute os tipos de triângulos, definindo-os por seus ângulos e lados. Ele descreve elementos-chave de triângulos como medianas, cevianas, incentro, baricentro, circuncentro e ortocentro. O documento também define triângulos inscritos em outros triângulos.