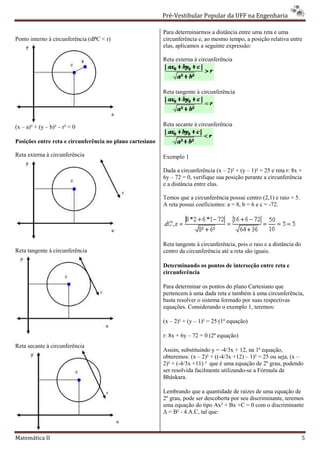
1) O documento apresenta os conceitos fundamentais de sistemas de coordenadas cartesianas no plano, incluindo distância entre pontos, equações de retas e circunferências.
2) É explicado como calcular a área de triângulos no plano cartesiano usando determinantes.
3) São descritas as posições relativas entre pontos, retas e circunferências no plano cartesiano.
![Pré-Vestibular Popular da UFF na Engenharia
ibular
UNIVERSIDADE FEDERAL FLUMINENSE Como:
DISCIPLINA: MATEMÁTICA II
PROFESSORA: JULIANA [d(P, R)]2 = | x1 - x2| 2 = (x1 - x2)2
Eixos Coordenados e
Consideremos um plano e duas retas perpendiculares, [d(Q,R)] 2 = | y1 - y2| 2 = (y1 - y2)2
sendo uma delas horizontal e a outra vertical. A horizontal
será denominada Eixo das Abscissas (eixo OX) e a Vertical
então
será denominada Eixo das Ordenadas (eixo OY). Os pares
ordenados de pontos do plano são indicados na forma
P=(x,y) onde x será a abscissa do ponto P e y a ordenada do
ponto P.
Exemplos: A distância entre P=(2,3) e Q=(5,12) é:
√(2-5)2 +(3-12)2 = √90 (raiz quadrada de 90)
90
A distância entre a origem O=(0,0) e um ponto P=(x,y) é
dada por:
Na verdade, x representa a distância entre as duas retas
verticais indicadas no gráfico e y é a distância entre as duas
retas horizontais indicadas no gráfico. O sistema de
Coordenadas Ortogonais é conhecido por Sistema de
Coordenadas Cartesianas e tal sistema possui quatro Ponto médio de um segmento
regiões denominadas quadrantes.
Aplicação: Dados os pares ordenados P=(x1,y1) e
Distância entre dois pontos do plano cartesiano Q=(x2,y2), pode-se obter o Ponto Médio M=(xm,ym) que
se
está localizado entre P e Q.
Teorema de Pitágoras: Em um triângulo retângulo, o
quadrado da medida da hipotenusa a é igual à soma dos
quadrados das medidas dos catetos b e c, isto é, a2=b2+c2.
Dados P=(x1,y1) e Q=(x2,y2), obtemos a distância entre P e O ponto médio é obtido com o uso da média aritmética,
Q, traçando as projeções destes pontos sobre os eixos uma vez para as abscissas e outra vez para as ordenadas.
coordenados, obtendo um triângulo retângulo e usando o
Teorema de Pitágoras. xm = (x1 + x2)/2, ym = (y1 + y2)/2
Observação: O centro de gravidade(ou Baricentro) de um
triângulo plano cujas coordenadas dos vértices são
rdenadas
A=(x1,y1), B=(x2,y2) e C=(x3,y3), é:
G=((x1+x2+x3)/3, (y1+y2+y3)/3 )
O segmento PQ é a hipotenusa do triângulo retângulo PQR,
o segmento PR é um cateto e o segmento QR é o outro Retas no plano cartesiano
cateto, logo:
Na Geometria Euclidiana, dados dois pontos P1=(x1,y1) e
2 2
[d(P,Q)] = [d(P,R)] + [d(Q,R)] 2 P2=(x2,y2) no plano cartesiano, existe uma única reta que
passa por esses pontos. Para a determinação da equação de
uma reta existe a necessidade de duas informações e dois
Matemática II 1](https://image.slidesharecdn.com/apostilamat2-100801074308-phpapp01/75/Apostila-mat2-1-2048.jpg)






![Pré-Vestibular Popular da UFF na Engenharia
ibular
Seja a PA genérica (a1, a2, a3, ... , an, ...) de razão r. 4 - Propriedades das Progressões Aritméticas
De acordo com a definição podemos escrever:
a2 = a1 + 1.r Numa PA, cada termo (a partir do segundo) é a média
a3 = a2 + r = (a1 + r) + r = a1 + 2r aritmética dos termos vizinhos deste.
a4 = a3 + r = (a1 + 2r) + r = a1 + 3r
..................................................... Exemplo:
PA : ( m, n, r ) ; portanto, n = (m + r) / 2
Podemos inferir (deduzir) das igualdades acima que:
.............. an = a1 + (n – 1) . r Assim, se lhe apresentarem um problema de PA do tipo:
A expressão an = a1 + (n – 1) . r é denominada termo geral Três números estão em PA, .. , a forma mais inteligente de
...
da PA. resolver o problema é considerar que a PA é do tipo:
Nesta fórmula, temos que an é o termo de ordem n (n- (x - r, x, x + r), onde r é a razão da PA.
ésimo termo) , r é a razão e a1 é o primeiro termo da
Progressão Aritmética – PA. Numa PA, a soma dos termos eqüidistantes dos
extremos é constante.
Exemplos:
Exemplo:
Qual o milésimo número ímpar positivo? PA : ( m, n, r, s, t); portanto, m + t = n + s = r + r = 2r
Temos a PA: ( 1, 3, 5, 7, 9, ... ) onde o primeiro termo a1=
1, a razão r = 2 e queremos calcular o milésimo termo a1000. Estas propriedades facilitam sobremaneira a solução de
Nestas condições, n = 1000 e poderemos escrever: problemas.
a1000 = a1 + (1000 - 1).2 = 1 + 999.2 = 1 + 1998 = 1999.
Portanto, 1999 é o milésimo número ímpar.
5 - Soma dos n primeiros termos de uma PA
Qual o número de termos da PA: ( 100, 98, 96, ... , 22) ? Seja a PA ( a1, a2, a3, ..., an-1, an).
Temos a1 = 100, r = 98 -100 = - 2 e an = 22 e desejamos A soma dos n primeiros termos Sn = a1 + a2 + a3 + ... + an-1
calcular n. + an , pode ser deduzida facilmente, da aplicação da
Substituindo na fórmula do termo geral, fica: 22 = 100 + (n segunda propriedade acima.
- 1). (- 2) ;
logo, 22 - 100 = - 2n + 2 e, 22 - 100 - 2 = - 2n de onde
Temos:
conclui-se que - 80 = - 2n ,
Sn = a1 + a2 + a3 + ... + an-1 + an
de onde vem n = 40.
Portanto, a PA possui 40 termos.
É claro que também poderemos escrever a igualdade acima
como:
Através de um tratamento simples e conveniente da
Sn = an + an-1 + ... + a3 + a2 + a1
fórmula do termo geral de uma PA, podemos generaliza
generaliza-la
da seguinte forma:
Somando membro a membro estas duas i igualdades, vem:
2. Sn = (a1 + an) + (a2 + an-1) + ... + (an + a1)
Sendo aj o termo de ordem j (j-ésimo termo) da PA e ak o
ésimo
termo de ordem k ( k-ésimo termo) da PA, poderemos
ésimo
escrever a seguinte fórmula genérica: Logo, pela segunda propriedade acima, as n parcelas entre
aj = ak + (j - k).r parênteses possuem o mesmo valor ( são iguais à soma dos
termos extremos a1 + an ) , de onde concluímos
inevitavelmente que:
Exemplos:
2.Sn = (a1 + an).n , onde n é o número de termos da PA.
Se numa PA o quinto termo é 30 e o vigésimo termo é 60,
Daí então, vem finalmente que:
qual a razão?
Temos a5 = 30 e a20 = 60.
Pela fórmula anterior, poderemos escrever:
a20 = a5 + (20 - 5) . r e substituindo fica: 60 = 30 + (20 - 5).r
ndo
;
60 - 30 = 15r ; logo, r = 2. Exemplo:
Calcule a soma dos 200 primeiros números ímpares
Numa PA de razão 5, o vigésimo termo vale 8. Qual o positivos.
terceiro termo? Temos a PA: ( 1, 3, 5, 7, 9, ... )
Temos r = 5, a20 = 8. Precisamos conhecer o valor de a200 .
Logo, o termo procurado será: a3 = a20 + (3 – 20).5 Mas, a200 = a1 + (200 - 1).r = 1 + 199.2 = 399
a3 = 8 –17.5 = 8 – 85 = - 77. Logo, Sn = [(1 + 399). 200] / 2 = 40.000
Matemática II 9](https://image.slidesharecdn.com/apostilamat2-100801074308-phpapp01/85/Apostila-mat2-9-320.jpg)
![Pré-Vestibular Popular da UFF na Engenharia
ibular
Portanto, a soma dos duzentos primeiros números ímpares 2x – (x + 1) = (x2 – 5) – 2x
positivos é igual a 40000. 2x – x –1 + 5 – x2 + 2x = 0
3x + 4 – x2 = 0
Exercícios resolvidos e propostos:
Multiplicando por (-1) ambos os membros da igualdade
1)
1 - Qual é o número mínimo de termos que se deve somar acima, fica:
na P.A. :( 7/5 , 1 , 3/5 , ... ) , a partir do primeiro termo, x2 – 3x – 4 = 0
para que a soma seja negativa? Resolvendo a equação do segundo grau acima
*a) 9 encontraremos x = 4 ou x = - 1.
b) 8
c) 7 Assim, teremos:
d)6 x = 4: os termos da P.A . serão: x+1, 2x, x2 – 5 ou
e) 5 substituindo o valor de x encontrado: 5, 8, 11, que são as
medidas dos lados do triângulo. Portanto, o perímetro do
SOLUÇÃO: triângulo (soma das medidas dos lados) será igua a
igual
Temos: a1 = 7/5 e r = 1 – 7/5 = 5/5 – 7/5 = -2/5, ou seja: r = 5+8+11 = 24.
-2/5. O valor negativo de x não serve ao problema, já que levaria
Poderemos escrever então, para o n-ésimo termo an:
ésimo a valores negativos para os lados do triângulo, o que é uma
an = a1 + (n – 1).r = 7/5 + (n – 1).(-2/5) impossibilidade matemática, pois as medidas dos lados de
an = 7/5 – 2n/5 + 2/5 = (7/5 + 2/5) –2n/5 = 9/5 –2n/5 = (9 –
2n/5 um triângulo são necessariamente positivas. Portanto, a
2n)/5 alternativa correta é a letra D.
ativa
A soma dos n primeiros termos, pela fórmula vista 4 - UFBA - Numa progressão aritmética, o primeiro termo
anteriormente será então: é 1 e a soma do n-ésimo termo com o número de termos é
ésimo
Sn = (a1 + an). (n/2) = [(7/5) + (9 – 2n)/5].(n/2) = [(16 – 2. Calcule a razão dessa progressão.
2n)/5].(n/2) Resp: r = -1
Sn = (16n – 2n2) / 10
SOLUÇÃO:
Ora, nós queremos que a soma Sn seja negativa; logo, vem: Temos: a1 = 1 e an + n = 2, onde an é o n-ésimo termo.
(16n – 2n2) / 10 < 0 Fazendo n = 2, vem: a2 + 2 = 2, de onde vem
imediatamente que a2 = 0.
Como o denominador é positivo, para que a fração acima Daí, r = a2 – a1 = 0 – 1 = -1, que é a resposta procurada.
,
seja negativa, o numerador deve ser negativo. Logo,
deveremos ter: 1 – Definição
16n – 2n2 < 0
Entenderemos por progressão geométrica - PG - como
Portanto, n(16 – 2n ) < 0 qualquer seqüência de números reais ou complexos, onde
Ora, como n é o número de termos, ele é um número inteiro cada termo a partir do segundo, é igual ao anterior,
e positivo. Portanto, para que o produto acima seja multiplicado por uma constante denominada razão.
negativo, deveremos ter:
16 – 2n < 0, de onde vem 16 < 2n ou 2n > 16 ou n > 8. Exemplos:
Como n é um número inteiro positivo, deduzimos (1,2,4,8,16,32, ... ) PG de razão 2
imediatamente que n = 9. (5,5,5,5,5,5,5, ... ) PG de razão 1
Portanto, a alternativa correta é a letra A. (100,50,25, ... ) PG de razão 1/2
,25,
(2,-6,18,-54,162, ...) PG de razão -3
54,162,
2 - As medidas dos lados de um triângulo são expressas por
x + 1, 2x , x2 - 5 e estão em P.A. , nesta ordem. O perímetro 2 - Fórmula do termo geral
do triângulo vale:
a) 8 Seja a PG genérica: (a1, a2, a3, a4, ... , a n, ... ) , onde a1 é o
b) 12 primeiro termo, e an é o n-ésimo termo, ou seja, o termo de
ésimo
c) 15 ordem n. Sendo q a razão da PG, da definição podemos
*d) 24 escrever:
e) 33 a2 = a1 . q
a3 = a2 . q = (a1 . q) . q = a1 . q2
SOLUÇÃO: a4 = a3 . q = (a1 . q2) . q = a1 . q3
Ora, se x + 1, 2x , x2 – 5 formam uma P.A. , podemos ................................................
escrever: ................................................
Matemática II 10](https://image.slidesharecdn.com/apostilamat2-100801074308-phpapp01/85/Apostila-mat2-10-320.jpg)

![Pré-Vestibular Popular da UFF na Engenharia
ibular
Multiplicando ambos os membros por q, fica:
9 + 9q2 – 30q = 0
Dividindo por 3 e ordenando, fica:
3q2 – 10q + 3 = 0, que é uma equação do segundo grau. PENGE 1
Resolvendo a equação do segundo grau acima
encontraremos q = 3 ou q = 1/3.
1 .Conhecendo-se o baricentro B(3,5), do triângulo XYZ
se
Como é dito que a PG é decrescente, devemos considerar onde X(2,5), Y(-4,6), responda:
4,6),
apenas o valor a) Quais as coordenadas do vértice Z do triângulo
)
q = 1/3, já que para q = 3, a PG seria crescente. XYZ?
Portanto, a PG é:
9/q, 9, 9q, ou substituindo o valor de q vem: 27, 9, 3. b) Qual o comprimento do segmento BZ?
)
O problema pede a soma dos quadrados, logo:
a2 + b2 + c2 = 272 + 92 + 32 = 729 + 81 + 9 = 819 2. Seja a reta y = -2x, determine:
2x,
6.2 - Sabe-se que S = 9 + 99 + 999 + 9999 + ... + 999...9
se a) As coordenadas do ponto P que está no segundo
onde a última parcela contém n algarismos. Nestas quadrante, sobre a reta r e cuja distância ao ponto
condições, o valor de 10n+1 - 9(S + n) é: (0,-1) é √10 unidades;
10
A)1 b) As coordenadas do ponto Q, sobre a reta r, que esestá
*B) 10 mais próximo do ponto (0,(0,-1).
C) 100
D) -1
E) -10 PENGE 2
Solução: 1-Sendo o ponto P(r - 12, 4r - 6) pertencente a bissetriz dos
quadrantes ímpares e P’(s-12, 4s
12, 4s-13) pertencente a bissetriz
Observe que podemos escrever a soma S como:
rve dos quadrantes ímpares, determine:
S = (10 – 1) + (100 – 1) + (1000 – 1) + (10000 – 1) + ... +
(10n – 1)
a) O valor da distância entre P e P’.
S = (10 – 1) + (102 – 1) + (103 – 1) + (104 – 1) + ... + (10n –
1)
b) Qual dos pontos está mais próximo da origem.
ntos
Como existem n parcelas, observe que o número ( 1) é
(–
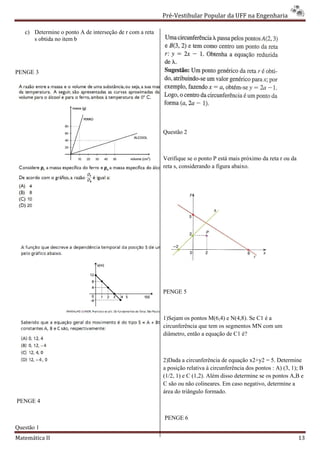
somado n vezes, 2. Considere o gráfico:
resultando em n(-1) = - n.
Logo, poderemos escrever:
S = (10 + 102 + 103 + 104 + ... + 10n ) – n
Vamos calcular a soma Sn = 10 + 102 + 103 + 104 + ... + 10n
, que é uma PG de primeiro termo a1 = 10, razão q = 10 e
último termo an = 10n . Teremos:
Sn = (an.q – a1) / (q –1) = (10n . 10 – 10) / (10 – 1) = (10n+1 –
10) / 9
Substituindo em S, vem:
S = [(10n+1 – 10) / 9] – n
Deseja-se calcular o valor de 10n+1 - 9(S + n)
Temos que S + n = [(10n+1 – 10) / 9] – n + n = (10n+1 – 10) /
9 a) Obtenha uma equação da reta r
Substituindo o valor de S + n encontrado acima, fica:
10n+1 – 9(S + n) = 10n+1 – 9(10n+1 – 10) / 9 = 10n+1 – (10n+1 – b) Obtenha uma equação da reta s que passa por P e é
10) = 10 perpendicular a r.
Matemática II 12](https://image.slidesharecdn.com/apostilamat2-100801074308-phpapp01/85/Apostila-mat2-12-320.jpg)