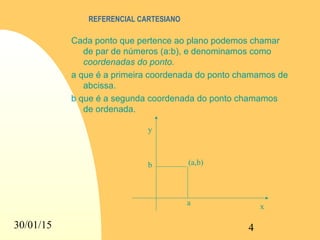
O documento explica o referencial cartesiano, que consiste em dois eixos perpendiculares (x e y), onde o eixo vertical é chamado de ordenadas e o horizontal de abcissas. Cada ponto no plano cartesiano é representado por um par de números correspondentes às suas coordenadas x e y.

1. 30/01/15 1
REFERENCIAL
CARTESIANO
Aula 1
Professora Renata Dias Melo Varella

2. 30/01/15 2
Introdução
No estudo da Matemática para se localizar os pontos
no plano é necessário utilizar o termo:
REFERENCIAL CARTESIANO
Y
X

3. 30/01/15 3
REFERENCIAL CARTESIANO
O gráfico cartesiano possui dois eixos que são
perpendiculares entre si. Podemos visualizar
abaixo:
y
Eixo das ordenadas
x
Eixo das abcissas
O eixo vertical é denominado como eixo das ordenadas e o
sentido dele vai de baixo para cima.
O eixo horizontal é denominado como eixo das abcissas e o
sentido dele vai da esquerda para a direita.
O ponto de encontro desses dois eixos podemos denominar
como origem.
0 origem

4. 30/01/15 4
REFERENCIAL CARTESIANO
Cada ponto que pertence ao plano podemos chamar
de par de números (a:b), e denominamos como
coordenadas do ponto.
a que é a primeira coordenada do ponto chamamos de
abcissa.
b que é a segunda coordenada do ponto chamamos
de ordenada.
y
xa
b (a,b)

5. 30/01/15 5
REFERENCIAL CARTESIANO
Podemos exemplificar da seguinte forma: Dada a
figura abaixo, sendo o ponto A formado pela
abcissa 3 e sua ordenada 2. Podemos dizer que
suas coordenadas são 3 e 2 e podem se
representadas por:
A (3,2)
No gráfico:
0 1 2 3
1
2 A

6. 30/01/15 6
CONCLUSÃO
Podemos dizer então que o chamado plano ou
referencial cartesiano baseia-se no encontro de
dois eixos, sendo estes eixos perpendiculares entre
si e sua junção será no ponto 0, que é a origem
destes dois pontos (x e y). O primeiro é o eixo das
abcissas e o segundo ponto é o eixo das
ordenadas.

7. 30/01/15 6
CONCLUSÃO
Podemos dizer então que o chamado plano ou
referencial cartesiano baseia-se no encontro de
dois eixos, sendo estes eixos perpendiculares entre
si e sua junção será no ponto 0, que é a origem
destes dois pontos (x e y). O primeiro é o eixo das
abcissas e o segundo ponto é o eixo das
ordenadas.