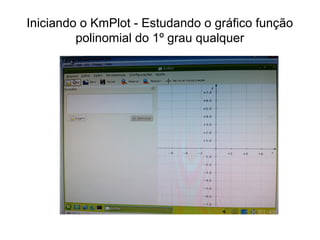
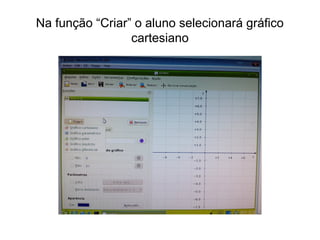
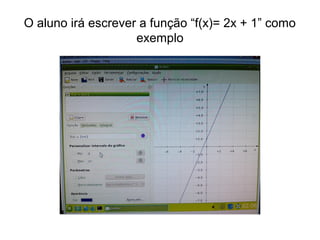
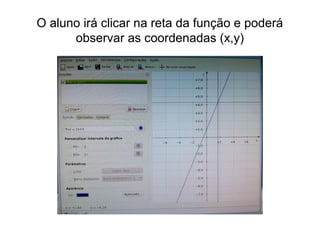
O documento descreve um curso sobre funções polinomiais do 1o grau ministrado em 6 aulas. A primeira aula apresenta dois problemas relacionados a planos de saúde e custos de produção para serem resolvidos usando funções do 1o grau. Nas aulas subsequentes são apresentados conceitos, construídos gráficos no software KmPlot e realizados exercícios para solidificar os conhecimentos.

1. FUNÇÃO POLINOMIAL
DO
1º GRAU
Curso de Informática Educativa I
Projeto Execução
Leandro Casemiro

2. Função Polinomial do 1º grau
Coeficientes
Gráficos
Aplicações

3. Antes da primeira aula serão feita algumas
revisões
Alguns temas serão relembrados:
Equações do 1º grau
Inequação do 1º grau
Intervalos e Sistemas

4. Primeira Aula – São propostos dois problemas
Responda :
1. Uma pessoa vai escolher um plano de saúde entre
duas opções: A e B.
Condições dos planos:
Plano A: cobra um valor fixo mensal de R$ 140,00 e
R$ 20,00 por consulta num certo período.
Plano B: cobra um valor fixo mensal de R$ 110,00 e
R$ 25,00 por consulta num certo período.
Em qual situação o plano A é mais econômico ? o
plano B é mais econômico ? os dois se equivalem ?

5. Primeira Aula – São propostos dois problemas
2. Na produção de peças, uma fábrica tem um custo fixo
de R$ 16,00 mais um custo variável de R$ 1,50 por
unidade produzida. Sendo x o número de peças
unitárias produzidas, qual seria o custo de produção de
400 peças ? E de 1000 peças ?
O que essas duas questões tem em comum ? Existe
alguma técnica para resolver estes problemas ?
Empregamos o conceito de função do 1º grau para
solucionar estes problemas.

6. Segunda Aula – Apresentando os conceitos e
definições sobre função polinomial do
1º grau
Na apresentação dos conceitos e definições
sobre função polinomial do 1º grau será
empregado o software KmPlot.
Esta aula será ministrada no laboratório de
informática com o uso do software KmPlot.
Algumas funções do software KmPlot serão
apresentados aos alunos para familiarização
dos recursos.

7. Terceira Aula – Estudando os gráficos da função
polinomial do 1º grau
Construções através do software KmPlot.
Coeficientes
Gráficos
Aplicações

8. Iniciando o KmPlot - Estudando o gráfico função
polinomial do 1º grau qualquer

9. Na função “Criar” o aluno selecionará gráfico
cartesiano

10. O aluno irá escrever a função “f(x)= 2x + 1” como
exemplo

11. O aluno irá clicar na reta da função e poderá
observar as coordenadas (x,y)

12. Na parte inferior esquerda poderá ver os valores
de x e y
O aluno após clicar na
reta, poderá observar
as diversas
coordenadas, por
exemplo: quando
x =1,64 então
y = 4,29.

13. Os alunos irão mudar o valor do coeficiente
angular a
Com isso poderão
observar que
declividade da reta.
Irão notar que quando
o coeficiente a for
positivo a função será
crescente e quando
negativo descrente.

14. Uma nova função será criada.
A função será f(x) = 5x – 2.

15. Diferenças das funções e suas retas
Uma nova função f(x) = 5x – 2 foi criada.
O aluno observará as diferenças das retas das
respectivas funções f(x) = -2x+1 e
f(x) = 5x - 2.

16. Retas das funções
O aluno observará a
reta da função
f(x) = -2x+1 na cor
azul e a reta da
função f(x) = 5x – 2
na cor vermelha

17. Quarta Aula – Pesquisa sobre o tema, função
polinomial do 1º grau, e discussão sobre os
recursos do KmPlot
Apresentação das pesquisas dos alunos.
Discussão dos recursos do KmPlot na
construção dos gráficos, declividade da reta,
coordenadas.
Realização de exercícios em grupo no
laboratório de informática.

18. Quinta Aula - Resolvendo o primeiro exercício
gerador do tema
Uma pessoa vai escolher um plano de saúde entre duas opções:
A e B.
Condições dos planos:
Plano A: cobra um valor fixo mensal de R$ 140,00 e R$ 20,00 por
consulta num certo período.
Plano B: cobra um valor fixo mensal de R$ 110,00 e R$ 25,00 por
consulta num certo período.
Em qual situação o plano A é mais econômico ? o plano B é mais
econômico ? os dois se equivalem ?
Resposta:
Primeiro determinaremos as leis das funções de cada plano :
Plano A: f(x) = 20x + 140
Plano B: g(x) = 25x + 110

19. Resolvendo o primeiro exercício gerador do tema
Para que o plano A seja mais econômico:
g(x) > f(x)
25x + 110 > 20x + 140
25x – 20x > 140 – 110
5x > 30
x > 30/5
x > 6

20. Resolvendo o primeiro exercício gerador do tema
Para que o Plano B seja mais econômico:
g(x) < f(x)
25x + 110 < 20x + 140
25x – 20x < 140 – 110
5x < 30
x < 30/5
x < 6

21. Resolvendo o primeiro exercício gerador do tema
Para que eles sejam equivalentes:
g(x) = f(x)
25x + 110 = 20x + 140
25x – 20x = 140 – 110
5x = 30
x = 30/5
x = 6

22. Resolvendo o primeiro exercício gerador do tema
Os alunos chegarão a seguinte conclusão :
O plano mais econômico será:
Plano A = quando o número de consultas for
maior que 6.
Plano B = quando número de consultas for
menor que 6.
Os dois planos serão equivalentes quando o
número de consultas for igual a 6.

23. Resolvendo o segundo exercício gerador do tema
Sendo x o número de peças unitárias
produzidas, qual seria o custo de produção de
400 peças ? E de 1000 peças ?
Primeiro determinaremos a lei da respectiva
função :
f(x) = 1,5x + 16

24. Resolvendo o segundo exercício gerador do tema
Na produção de peças, uma fábrica tem um custo fixo de R$ 16,00
mais um custo variável de R$ 1,50 por unidade produzida. Sendo x
o número de peças unitárias produzidas, qual seria o custo de
produção de 400 peças ? E de 1000 peças ?
Resposta:
Calculando primeiramente o custo de produção de 400 peças.
f(x) = 1,5x + 16
f(400) = 1,5*400 + 16
f(400) = 600 + 16
f(400) = 616 reais

25. Resolvendo o segundo exercício gerador do tema
Em seguida, calculamos o o custo de produção de 1000
peças ?
f(x) = 1,5x + 16
f(1000) = 1,5*1000 + 16
f(1000) = 1500 + 16
f(1000) = 1516 reais

26. Exercícios Propostos
1. Utilizando o software
Kmplot, construa os
gráficos das funções
f(x) = 2x - 4 e g(x) = -4x + 3.
Resposta ao lado!

27. Exercícios Propostos
1.1 Sabendo que toda função afim é determinada pela lei
f(x) = ax +b, com a e b números reais, em que a é o
coeficiente angular e b é o coeficiente linear da função.
Qual é o valor do coeficiente angular da função f(x) = 2x
- 4? Ele é positivo ou negativo?
Resposta: 2. Positivo.
Qual é o valor do coeficiente angular da função g(x) =
-4x + 3?
Ele é positivo ou negativo?
Resposta: -4. Negativo.

28. Exercícios Propostos
1.2 Observando os gráficos das funções f(x) e
g(x), determine qual função é
crescente e qual é decrescente.
f(x) = crescente
g(x) = decrescente

29. Exercícios Propostos
1.3 Agora com base na função f(x) = 2x - 4, crie mais dois
gráficos alterando apenas o valor do coeficiente angular
da função, mantendo este valor positivo. Estas novas
funções são crescentes ou decrescentes?
Resposta : crescentes
1.4 Observando agora a função g(x) = - 4x + 3 (que já está
na sua tela) construa mais dois gráficos alterando
apenas o valor do coeficiente angular da função,
mantendo este valor negativo. Estas novas funções são
crescentes ou decrescentes?
Resposta : decrescentes

30. Exercícios Propostos
1.5 Comparando as respostas encontradas nos
itens 1.3 e 1.4, o que você pode descrever com
relação ao coeficiente angular (ser positivo ou
ser negativo) e o crescimento ou decrescimento
destas funções.
Resposta : quando positivo função crescente e
quando negativo função decrescente.

31. Exercícios Propostos
2. Solicite um arquivo novo,
para isso clique na Barra
de Ferramentas em
Arquivo, e em seguida
em Novo. Construa
novamente os gráficos
das funções: f(x) = 2x - 4
e
g(x) = -4x + 3

32. Exercícios Propostos
2.1 Anote o valor da coordenada onde o gráfico de f(x)
corta o eixo x.
Resposta: (2,0)
2.2 Determine algebricamente o valor de x quando f(x) = 0.
Ou seja o zero ou raiz de f(x).
Resposta: 2x-4 = 0
x = 4: 2
x = 2
2.3 Compare as respostas encontradas nos itens 2.1 e 2.2
e descreva o que você observou.
Resposta: Quando x = 2 então y = 0.

33. Exercícios Propostos
2.4 Anote o valor da coordenada onde o gráfico de
g(x) corta o eixo x.
Resposta: (34,0)
2.5 Determine algebricamente o valor de x quando
g(x) = 0. Ou seja o zero ou raiz de g(x).
Resposta: -4x + 3 = 0
x = 34

34. Exercícios Propostos
2.6 Compare as respostas encontradas nos itens 2.4 e 2.5
e descreva o que você observou.
Resposta: Quando x = 2 então y = 0.
2.7 Anote o valor da coordenada onde o gráfico de f(x)
corta o eixo y.
Resposta: - 4
2.8 Determine o valor do coeficiente linear, ou seja, o valor
de b na função f(x) = 2x - 4
Resposta: - 4

35. Exercícios Propostos
2.9 Compare as respostas encontradas nos itens
2.8 e 2.9 e descreva o que você observou.
Resposta: b determina onde o eixo y será cortado.
2.10 Anote o valor da coordenada onde o gráfico
de g(x) corta o eixo y.
Resposta: (0,3)

36. Exercícios Propostos
2.11 Determine o valor do coeficiente linear, ou
seja, o valor de b na função g(x) = - 4x + 3
Resposta: 3
2.12 Compare as respostas encontradas nos itens
2.11 e 2.12 e descreva o que você observou.
Resposta: b determina onde o eixo y será cortado.

37. Sexta Aula : Avaliação das tarefas desenvolvidas
Avaliação dos Alunos:
Avaliação dos conhecimentos adquiridos e
participação do aluno no processo das suas
aprendizagens significativas.

38. Referência Bibliográfica
Disponível em, <
http://www.brasilescola.com/matematica/aplicacoes-uma-funcao-.htm>. Acessado em 02/08/2014.
Disponível em, <
http://pt.slideshare.net/scmaedu/anlise-de-dados-na-fsica-grficos
>. Acessado em 02/09/2014.
Disponível em, <
http://www.conexaoprofessor.rj.gov.br/downloads/cm/cm_11_>. Acessado em 02/08/2014.
Disponível em,
< http://pt.slideshare.net/luisadr/projeto-planejamento-luis-alberto->. Acessado em 02/09/2014.