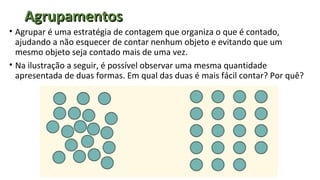
Este documento discute conceitos matemáticos como quantificação, registro, agrupamentos e contagem. Ele oferece atividades para crianças desenvolverem percepção numérica e senso de quantidade, além de reflexões sobre como agrupamentos podem facilitar a contagem de grandes coleções. O documento também discute a importância dos registros dos alunos para analisar seu progresso no aprendizado de conceitos matemáticos.

1. LEITURA DELEITELEITURA DELEITE
Diário de Biloca
Edson Gabriel Garcia
Ilustrações de Ricardo Azevedo
Nosso diário de
bordo

2. CADERNO 2CADERNO 2
QUANTIFICAÇÃO,QUANTIFICAÇÃO,
REGISTRO EREGISTRO E
AGRUPAMENTOSAGRUPAMENTOS
parte 1parte 1
O. E. Profª Arianna Peliciari Tinelli Busch
11/08/2014

3. O objetivo geral do caderno éO objetivo geral do caderno é provocar reflexões sobre aprovocar reflexões sobre a
ideia de número e seus usos em situações do cotidianoideia de número e seus usos em situações do cotidiano,,
oferecendo subsídios para práticas pedagógicas de modooferecendo subsídios para práticas pedagógicas de modo
que a criança possa:que a criança possa:

4. CONTAGEM
• Pegue lápis e papel;
• Observe os quadros que a Orientadora de Estudos irá mostrar;
• Anote a quantidade que você observou;
• Socialize.
• Quais foram os números mais fáceis de serem contados?
• Por quê?
• As crianças chegam à escola sem percepção numérica?
• Leitura do texto da página 7.

6. Perceber e relacionar quantidades até 5 é uma das
capacidades inatas de nós seres humanos e animais.
Independente de como estão organizadas.

7. SENSO NUMÉRICOSENSO NUMÉRICO
• O senso numérico é a capacidade que permite diferenciar, sem
contar, pequenas quantidades de grandes quantidades, perceber
onde há mais e onde há menos, quando há “tantos quantos” ou
uma situação de igualdade entre dois grupos. O senso numérico é a
capacidade natural que o ser humano e alguns animais possuem
para apropriar-se de quantidades, ou seja, num golpe de vista
consegue-se indicar quantidades pequenas, de um a cinco, mesmo
que estas se refiram a objetos ou seres que podem estar em
movimento, como animais ou aves em um pasto. (pág. 6 – caderno
2)

9. O que é correspondência um a um?
• Correspondência um a um é a relação que se estabelece na
comparação unidade a unidade entre os elementos de duas coleções.
• No controle de quantidades por meio da correspondência um a um,
para cada elemento de uma coleção que se deseja contar, existe
outro elemento de outra coleção...
• A correspondência uma a um é também utilizada por nos no dia a dia.
Como por ex: quando andamos de ônibus.(pág. 11)
• Da mesma forma, a criança na escola pode fazer registros de
quantidades sem conhecer os símbolos numéricos que utilizamos
atualmente.

10. Onde tem
mais?

11. Cenas e quantidadesCenas e quantidades
PERCEBER A IDEIA DE TANTOS A MAIS.
SERÁ QUE ISSO É FACIL PARA AS CRIANÇAS?
• TRABALHAR PRIMEIRAMENTE COM MATERIAIS MANIPULÁVEIS, PARA
LEVAR AS CRIANÇAS A PERCEBEREM O NUMERO, A QUANTIDADE, PARA
DEPOIS PARTIR PARA UMA REPRESENTAÇÃO ESCRITA.

12. Que dinâmicas proporcionar aos
meus alunos, para dar
oportunidade à eles de fazerem
comparações para determinar onde
há mais, onde há menos ou há
tantos quantos, em comparação de
quantidade de objetos?

13. Represente com as pedras a imagem
abaixo

14. Mais representações usando as pedras

15. ContagemContagem
São três as condições para que o ser humano saiba de fato contar,
segundo Ifrah (1998).
•Ele deve ser capaz de atribuir um “lugar“ a cada ser que passa
diante dele; (aspecto ordinal)
•Ele deve ser capaz de intervir para introduzir na unidade que passa
a lembrança de todas que a precederam (aspecto cardinal)
•Ele deve saber conceber esta sucessão simultaneamente. (O que
chamamos de conservação das quantidades) Exemplos: calendários,
agenda, observação e contagem de horas.

16. O agrupamento na organização daO agrupamento na organização da
contagem e na origem dos sistemas decontagem e na origem dos sistemas de
numeraçãonumeração
Quando as crianças tentam contar usando os dedos das mãos, elas estão
descobrindo seu corpo como ferramenta para o processo de contagem, como
muitos povos fizeram ou ainda o fazem.
Por que as crianças contam nos dedos?

17. Onde você
guardaria
estes
produtos?
E se tivesse mais de um
destes produtos?
Você continuaria
guardando no mesmo
lugar? Por quê?
Se levarmos em conta os aspectos qualitativos
que nos fazem agrupar produtos na vida
cotidiana, concluiremos que o fazemos para:
Já pararam para pensar que muitos destes
produtos já foram agrupados antes que os
adquiríssemos?
Vamos observar alguns exemplos...

18. Há situações em que encontramos
diferentes agrupamentos...
2 em 2 3 em 3
5 em 5
4 em 4
6 em 6

19. 8 em 8 10 em 10 12 em 12
100 em
100 E etc...
Há situações em que encontramos
diferentes agrupamentos...
Como você faria se
precisasse organizar algum
destes produtos em grande
quantidade?

20. Uma vivência para refletirmos...
Como você agruparia estes objetos em cada
espaço?
Há apenas uma possibilidade?
Então, quer dizer que o
agrupamento pode nos ajudar a
organizar melhor nossos produtos...
E também podemos fazê-lo de 2 em
2, 3 em 3, 4 em 4, 5 em 5, em
Há ideias
matemáticas
envolvidas
nestes
agrupamentos?

21. Como você contaria os itens abaixo, sem perder
a “conta”?
• 1 a 1?
• de 2 em 2?
• de 5 em 5?
• de 10 em 10?
• de outra
Será que já
chegamos a
algumas
conclusões?

22. AgrupamentosAgrupamentos
• Agrupar é uma estratégia de contagem que organiza o que é contado,
ajudando a não esquecer de contar nenhum objeto e evitando que um
mesmo objeto seja contado mais de uma vez.
• Na ilustração a seguir, é possível observar uma mesma quantidade
apresentada de duas formas. Em qual das duas é mais fácil contar? Por quê?

23. Como será que os
conhecimentos de
quantificação e agrupamentos foram
registrados nos tempos antigos?
E como isso se dá com cada
criança?
REFLETINDO...REFLETINDO...

24. A necessidade de contar grandes quantidades levou o ser humano a superar a
correspondência um a um e organizar “montes” ou “grupos” de quantidades,
ou seja, a contagem por agrupamento. Esse tipo de contagem é o princípio
básico que deu origem aos mais diversos sistemas de numeração. A contagem
por agrupamento representou um grande avanço, pois permitiu ao ser
humano superar a correspondência um a um, tornando a ação de contagem
de grandes quantidades mais rápida e eficiente. (pág. 15)

25. • Contar e agrupar são ações que permitem controlar, comparar e
representar quantidades. Daí a importância de propor atividades para os
alunos que exijam a contagem de uma coleção de objetos por meio de seu
agrupamento em quantidades menores.
• Leitura do relato de experiência: O sítio animado – pág. 16
• A história apresentada é imaginária, os personagens são animais que
falam e contam. Ela seria adequada para os seus alunos?
• De que outras maneiras você poderia desenvolver um trabalho com outras
situações que levassem seus alunos a fazer agrupamentos para facilitar a
contagem e representar grandes quantidades com pouco material?

26. O ato de contar (quantificar) por si só, a depender da situação
colocada, já traz ações do campo aditivo e multiplicativo.
Se valorizarmos os agrupamentos como estratégia para contar
oportunizaremos aos alunos o desenvolvimento de conceitos
fundamentais para a realização de cálculos. São exemplos:
• Juntar e Separar elementos;
• Decompor e compor
quantidades;
• Organizar parcelas iguais;
• Contar em escalas crescentes
variadas;
• Dividir um todos em partes
iguais;
Para fechar...

27. PAREAMENTOPAREAMENTO
O pareamento ocorre a partir da relação entre duas
coleções.
O trabalho com o pareamento possibilita melhor compreensão do conceito a mais.

28. OS REGISTROS DOS ALUNOSOS REGISTROS DOS ALUNOS
• Quadro na página 19
• Os registros apresentados em todos os cadernos são fundamentais
para dar ao professor condições de analisar o progresso dos alunos
na compreensão das ideias matemáticas.