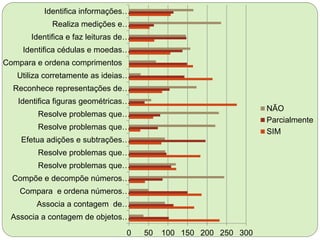
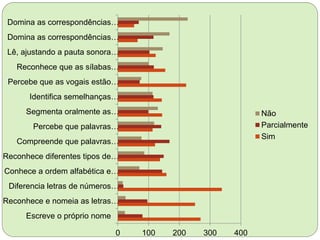
O documento analisa os perfis de entrada de matemática e linguagem de alunos do 1o ciclo do ensino fundamental de escolas municipais de Pontes e Lacerda. Apresenta dados sobre as habilidades dos alunos em contar, comparar números, resolver problemas matemáticos e reconhecer letras e palavras. Também fornece sugestões de atividades para o desenvolvimento do senso numérico e da alfabetização.





























![O AGRUPAMENTO NA ORGANIZAÇÃO DA CONTAGEM
E NA ORIGEM DOS SISTEMAS DE NUMERAÇÃO
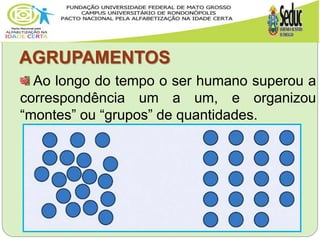
“[...] a necessidade de contar grandes
quantidades levou o ser humano a
superar a correspondência um a um
e organizar “montes” ou “grupos” de
quantidades, ou seja, a contagem por
agrupamento. Esse tipo de contagem
é o princípio básico que deu origem
aos mais diversos sistemas de
numeração.” (p. 15).](https://image.slidesharecdn.com/caderno2-140520215042-phpapp02-140725221701-phpapp01/85/Caderno2-140520215042-phpapp02-35-320.jpg)

















![USO E FUNÇÕES DO NÚMERO
EM SITUAÇÕES DO COTIDIANO
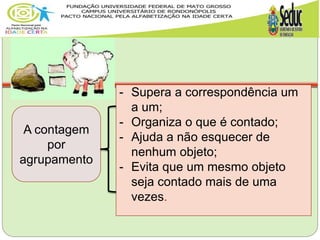
[...] desde muito cedo somos capazes de
discriminar quantidades pequenas através
de uma discriminação visual que nos
habilita a detectar até três elementos
mesmo sem realizar qualquer tipo de
contagem.](https://image.slidesharecdn.com/caderno2-140520215042-phpapp02-140725221701-phpapp01/85/Caderno2-140520215042-phpapp02-54-320.jpg)