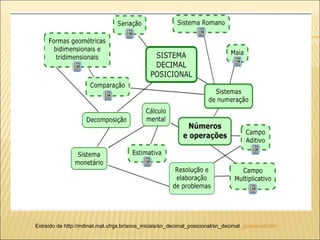
1) O documento discute habilidades matemáticas e estratégias de contagem, como agrupamento e sistemas de numeração. 2) É importante que as crianças desenvolvam a compreensão de quantidades ao contar objetos e associar nomes de números à sua ordem correta. 3) A atividade proposta pede que os alunos escrevam todos os modos de obter 9 através da soma de dois algarismos para explorar a propriedade comutativa e o elemento neutro da adição.

1. SME – Campinas / PNAIC
Slides elaborados por Adriana Correia
Coodernadora geral: Bete Pimentel
Colaboradoras: Cristina Pauluci, Eliana Boscolo, Idelvandre,Isnary, Ìtala
Rizzo, Kelly Arduíno, Laís Alendes,
Patrícia Regina Infanger Campos.
AGOSTO / 2014

2.  Leitura deleite
 Socialização dos trabalhos com as SDs (quais
atividades, grupos, etc). Aproximadamente 20
minutos.
 Início do trabalho com o tema de hoje.

3. Jérôme Bosch (creditado), O concerto do ovo, século XV, óleo sobre tela

4. Extraído da Revista "Enigma da Arte + 90 jogos com obras e artistas históricos" - Coquetel

5.  É uma habilidade que permite que o indivíduo lide de forma bem sucedida e
flexível com os vários recursos e situações do cotidiano que envolvem
a matemática.
 É uma boa intuição sobre números, sobre seus diferentes significados,
seus usos e funções; uma intenção de atribuir significado para as
situações numéricas.
 É algo que se desenvolve gradualmente sem se limitar ao uso dos algoritmos
tradicionais ou à formalização própria do contexto escolar.
 Não se trata de uma unidade curricular ou um conceito matemático que possa ser
diretamente ensinado, mas uma forma de pensar que deve permear as
situações de ensino em relação a todos os campos da matemática em
todos os segmentos da escolarização, desde a educação infantil.

6. COMO PODEMOS
CONTAR ESTE
CONJUNTO DE
BOLINHAS DE GUDE?

7. Atribuir a cada um dos objetos de uma coleção
uma palavra ou símbolo que corresponde a
uma posição na sequência numérica e que
indica a quantidade que ele representa nessa
posição.

8. Superaram a correspondência um a um e
organizaram “montes” ou “grupos” de
quantidades, ou seja, a contagem por
agrupamento. Esse tipo de contagem é o
princípio básico que deu origem aos
mais diversos sistemas de numeração.

9. São formas de organização que ao mesmo
tempo em que favorecem as contagens,
proporcionam o desenvolvimento dos sistemas
de numeração.

10. Agrupar é uma estratégia de contagem que organiza
o que é contado, ajudando a não esquecer de contar
nenhum objeto e evitando que um mesmo objeto
seja contado mais de uma vez.
Contar e agrupar são ações que permitem controlar,
comparar e representar quantidades. Por isso, a
importância de propor atividades para os alunos que
exijam a contagem de uma coleção de
objetos por meio de seu agrupamento em
quantidades menores.

11.  Tem esse nome por ser organizado na base 10 (de
origem provavelmente ligada às contagens que os
homens primitivos faziam com os dez dedos das
mãos).
 É posicional porque o valor de cada algarismo
depende do lugar que ele ocupa na escrita.
Par tindo da primeira casa, da direita para
a esquerda, cada posição é determinada
pela multiplicação do algarismo por uma
potência de 10 (1, 10, 100, 1000...).

12. A origem do número 52 em nosso sistema é
dada pela representação:
5 x 10 + 2 x 1 = 50 + 2 = 52
Já a representação do número 436 é:
4 x 100 + 3 x 10 + 6 x 1 =
400 + 30 + 6 = 436

13. Extraído de http://mdmat.mat.ufrgs.br/anos_iniciais/sn_decimal_posicional/sn_decimal_posicional.htm

14. https://www.youtube.com/watch?v=9VqPW8FfOnM

15. 1)
2)
3)...

16. O desenvolvimento da habilidade de contagem ganha
corpo quando ocorre a compreensão de quantidades e
para isso a criança deve:
a) fazer a associação dos nomes números de acordo com
a sua ordem (ordinalidade);
b) associar os nomes dos números com a identificação
dos elementos no conjunto (classificação);
c) contar somente uma vez cada elemento. Ao final da
contagem, a criança deverá perceber a correspondência
com o total de elementos pertencentes a coleção
quantificada.

18. É imprescindível saber que um número está
relacionado com o próximo pela adição do 1, 1
(+1), 2 (+1), 3 (+1), 4 (+1)...e assim por diante,
ou ligado ao anterior ao subtrair 1, isto é: 3 (–
1), 2 (–1), 1 (–1), 0.
A compreensão de sucessor e antecessor
são saberes importantes nas práticas de
contagem, recontagem e sobrecontagem.

20. Ela compreende a ordem, a inclusão e a conservação
das quantidades envolvidas na situação.
Este recurso subsidia o cálculo mental e pode ser
empregado ao fazer cálculos intermediários facilitando a
compreensão das técnicas operatórias, além de ser um
controle dos resultados para cálculos escritos. Por exemplo:
13 + 20 = 33 é o mesmo que
(10 + 10 + 10 + 3 = 33 ) ou
(10 + 20 = 30, 30 + 3 = 33).

21. Vamos escrever todos os modos possíveis para
obtermos o número 9 através da soma de 2
algarismos.
Atividade extraída do AM-2º ano do 1º grau-Vol. 1 - SEESSP - 1985

22. 9
9 + 0 = 9 0 + 9 = 9
8 + 1 = 9 1 + 8 = 9
7 + 2 = 9 2 + 7 = 9
6 + 3 = 9 3 + 6 = 9
5 + 4 = 9 4 + 5 = 9

23. Além das composições aditivas, essa atividade
explora inicialmente dois conceitos muito
importantes:
a) Propriedade comutativa: 1 + 8 = 8 + 1
b) Elemento neutro da adição (zero):
0 + 9 = 9 + 0

24. Vamos escrever todos os modos possíveis
para obtermos o número 10 através da
soma de até 3 algarismos.

26. Vamos socializar na lousa os direitos de
aprendizagem que vocês elencaram...

27. http://revistaescola.abril.com.br/fundamental-1/roteiro-didatico-sistema-Caderno 1 de apoio de aprendizagem da Prefeitura Municipal de
São Paulo (2010).
Cadernos 2 e 3 do PNAIC-Matemática (2014).
Caderno 1 do EMAI – SESSP (2014).
Cadernos do Mathema – Jogos de matemática do 1º ao 5º (Smole,
Diniz e Cândido). Artmed.