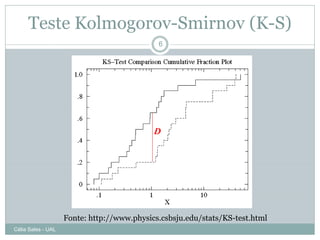
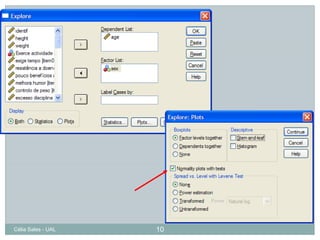
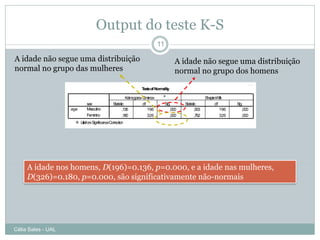
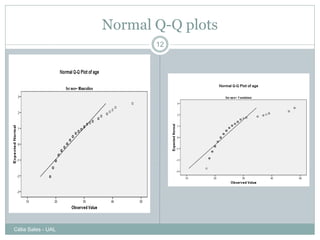
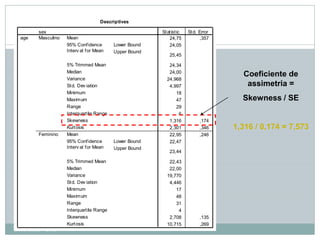
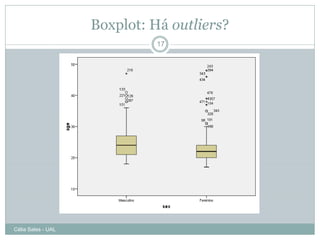
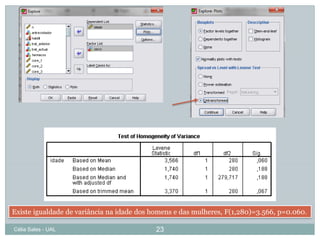
Este documento discute os pressupostos dos testes paramétricos, incluindo: 1) As amostras devem seguir uma distribuição normal; 2) Deve haver homogeneidade de variância entre os grupos; 3) As variáveis devem ser medidas em nível de intervalo ou razão. Métodos como gráficos Q-Q, teste Kolmogorov-Smirnov e coeficiente de assimetria são usados para verificar a normalidade, enquanto o teste de Levene é usado para verificar a homogeneidade de variância.

1. Pressupostos dos testes de hipóteses
paramétricos
PROFª DOUTORA CÉLIA SALES

2. Conteúdos
2
 Testes paramétricos
 Definição
 Análise de pressupostos mediante o SPSS
Célia Sales - UAL

3. Teste de hipóteses paramétrico
3
 Teste que requer dados de uma das distribuições
que é descrita pelos estatísticos (distribuição de
probabilidade)
 Geralmente, o termo “TESTE PARAMÉTRICO” é
usado para designar “TESTE PARAMÉTRICO
BASEADO NA DISTRIBUIÇÃO NORMAL”
Célia Sales - UAL

4. Pressupostos dos testes paramétricos
(baseados na distribuição normal)
4
Um teste paramétrico requer quatro características:
1. Distribuição de amostragem segue uma
distribuição normal (“normalidade dos dados”)
2. Homogeneidade da variância
3. Nível de medição da variável de intervalo ou
razão
4. Independência
Célia Sales - UAL

5. PASSO 1:
Verificação da Normalidade dos Dados
5
Considerar, para cada grupo a comparar:
1. Representação gráfica: dá-nos uma ideia da distribuição
dos dados (Q-Q plots)
2. Teste K-S de aderência à normalidade: testa se a diferença
entre a nossa distribuição e a distribuição normal é
SIGNIFICATIVA
3. Coeficiente de Assimetria
4. Dimensão dos grupos a comparar: Simplifica os passos
anteriores, para amostras grandes (Teorema do Limite
Central)
Célia Sales - UAL

6. Teste Kolmogorov-Smirnov (K-S)
6
Fonte: http://www.physics.csbsju.edu/stats/KS-test.html
Célia Sales - UAL

7. Teste Kolmogorov-Smirnov (K-S)
7
H0: A idade tem uma distribuição normal no grupo
dos homens
H1: A idade não tem uma distribuição normal no
grupo dos homens
 p<α Rejeita-se H0
A idade dos homens não segue uma distribuição normal
 p≥α Verifica-se o pressuposto da normalidade
A idade dos homens segue uma distribuição normal
Célia Sales - UAL

8. Coeficiente de assimetria
8
 O Teste K-S é conservador, isto é, tende a rejeitar a
hipótese nula quando ela é verdadeira (i.e., indicar
que os dados não seguem uma distribuição normal,
quando na realidade seguem)
 Se K-S rejeitar a hipótese nula, observar também o
coeficiente de assimetria, em cada grupo
 A partir do quadro do “Explore”, dividir a assimetria
(skweness) pelo seu Erro Padrão de Medida (SE)
Célia Sales - UAL

9. Verificação do pressuposto da normalidade no
SPSS
9
Analyse – descriptive statistics – explore
(normality plots with tests)
Vai dar-nos, para os grupos a comparar:
- Boxplots
- Normal Q-Q plots
- Teste K-S
- Quadro de estatísticas descritivas
Célia Sales - UAL

10. Célia Sales - UAL 10

11. Output do teste K-S
11
A idade não segue uma distribuição A idade não segue uma distribuição
normal no grupo das mulheres normal no grupo dos homens
T of Normality
ests
a
Kolmogorov-Smirnov Shapiro-Wilk
sex Statistic df Sig. Statistic df Sig.
age M lino
ascu ,136 196 ,000 ,903 196 ,000
Feminino ,180 326 ,000 ,762 326 ,000
a. Lilliefo SignificanceCorrectio
rs n
A idade nos homens, D(196)=0.136, p=0.000, e a idade nas mulheres,
D(326)=0.180, p=0.000, são significativamente não-normais
Célia Sales - UAL

12. Normal Q-Q plots
12
Célia Sales - UAL

13. Descriptives
sex St at ist ic St d. Error
age Masculino Mean 24,75 ,357
95% Conf idence Lower Bound 13 24,05
Interv al f or Mean Upper Bound
25,45
5% Trimmed Mean 24,34
Median 24,00
Variance
Coeficiente de
24,968
St d. Dev iation 4,997 assimetria =
Minimum 18
Maximum 47 Skewness / SE
Range 29
Interquart ile Range 6
Skewness 1,316 ,174
Kurt osis 2,301 ,346 1,316 / 0,174 = 7,573
Feminino Mean 22,95 ,246
95% Conf idence Lower Bound 22,47
Interv al f or Mean Upper Bound
23,44
5% Trimmed Mean 22,43
Median 22,00
Variance 19,770
St d. Dev iation 4,446
Minimum 17
Maximum 48
Range 31
Interquart ile Range 4
Skewness 2,708 ,135
Kurt osis 10,715 ,269
Célia Sales - UAL

14. Interpretação do coeficiente de assimetria
14
 Valor estandardizado (Z-score)
< -2 ou >2
os dados não seguem uma distribuição normal
Célia Sales - UAL

15. Teorema do Limite Central
15
1. Quando as amostras são grandes (n > 30), a
distribuição de tende a seguir uma distribuição
normal, independentemente da forma da
população de onde a amostra é retirada
 Importante para verificação do pressuposto de normalidade
2. O desvio padrão da distribuição de amostragem
(i.e., o Erro Padrão, SE) é igual ao desvio padrão da
amostra a dividir pela raíz quadrada da dimensão
da amostra (N)
Célia Sales - UAL

16. Teorema do Limite Central e testes paramétricos
16
 Se os grupos a comparar tiverem (cada um) n>30,
podemos assumir a normalidade dos dados
 Não são necessários os passos anteriormente vistos (K-S,
coeficiente de assimetria)
 No entanto, é indispensável observar se há outliers;
se sim, a média pode não ser a melhor medida para
comparar os grupos
Célia Sales - UAL

17. Boxplot: Há outliers?
17
Célia Sales - UAL

18. Em suma: Passo 1 - Verificação da
normalidade de cada grupo a comparar
18
 Gráfico Q-Q
 se os pontos se situam na linha recta, é indicativo de distribuição
normal
 K-S de adesão à normal
 Coeficiente de assimetria
 se se situar entre -2 e 2, podemos assumir que a distribuição é
normal
 Teorema do Limite Central
 Boxplot
 Se houver outliers, a média não é um bom modelo da distribuição –
o teste t poderá ser desaconselhado
(no caso de comparação de médias)
Célia Sales - UAL

19. Pressupostos dos testes paramétricos
(baseados na distribuição normal)
19
Um teste paramétrico requer quatro características:
1. Distribuição de amostragem segue uma
distribuição normal
2. Homogeneidade da variância
3. Nível de medição da variável de intervalo ou
razão
4. Independência
Célia Sales - UAL

20. Homogeneidade da variância
20
 Em testes de comparação de grupos de participantes,
significa que cada amostra provém de populações com a
mesma variância
 A homogeneidade da variância de grupos de participantes
verifica-se com o teste Levene
Célia Sales - UAL

21. Teste Levene
 Testa a hipótese nula de que a variância entre
os grupos é igual.
 Se:
p<α Variâncias são significativamente
diferentes – NÃO HÁ homogeneidade
p≥α Há homogeneidade
Para reportar: F(df1, df2) = value, Sig
21

22. Teste Levene no SPSS
22
 Geralmente é calculado juntamente com os testes que o
exigem (por exemplo, t-student)
 Podemos calculá-lo separadamente:
ANALYSE – DESCRIPTIVE STATISTICS – EXPLORE
Dependent List: variável cuja média pretendemos comparar
Factor List: variável de definição dos grupos a comparar
Plots:
 Boxplots: Factor levels together
 Spread vs. Plots with Levene Test: Untransformed
Célia Sales - UAL

23. Existe igualdade de variância na idade dos homens e das mulheres, F(1,280)=3.566, p=0.060.
Célia Sales - UAL 23

24. Pressupostos dos testes paramétricos
(baseados na distribuição normal)
24
Um teste paramétrico requer quatro características:
1. Distribuição de amostragem segue uma
distribuição normal
2. Homogeneidade da variância
3. Nível de medição da variável de intervalo ou
razão
4. Independência
Célia Sales - UAL

25. Nível de medição da variável
25
 Em teoria, apenas os dados de natureza contínua (de
intervalo ou de razão) poderão seguir uma distribuição
normal
 EXCEPÇÃO para os dados ORDINAIS (Labowitz,
1967; 1970)
 Com muitas possibilidades de resposta (5 ou mais)
 A distância entre os níveis de resposta é igual entre cada nível
de resposta
 Escalas de Likert com 5 ou mais níveis, podem ser tratados
com testes de hipótese paramétricos (escalas de quasi-
intervalo)
Célia Sales - UAL

26. Pressupostos dos testes paramétricos
(baseados na distribuição normal)
26
Um teste paramétrico requer quatro características:
1. Distribuição de amostragem segue uma
distribuição normal
2. Homogeneidade da variância
3. Nível de medição da variável de intervalo ou
razão
4. Independência
Célia Sales - UAL

27. Leituras de apoio
27
 Field (2010), cap. 5
Célia Sales - UAL