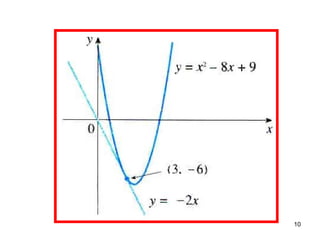
O documento discute a interpretação da derivada de uma função como a inclinação da reta tangente ao gráfico da função em um ponto e como a taxa instantânea de variação de y em relação a x no ponto. Ele fornece exemplos para calcular a derivada de uma função parabólica e encontrar a equação da reta tangente.

1. DERIVADA
A Derivada de uma função f pode ser
interpretada como:
1- Uma função cujo valor em x é a Inclinação
da Reta Tangente ao gráfico de y = f(x) em x,
ou
2- Uma função cujo valor em x é a taxa
instantânea de variação de y em relação à x,
no ponto x.
1

2. INTERPRETAÇÃO DA
DERIVADA
COMO A INCLINAÇÃO
DA RETA TANGENTE
Profa. Rosana G. S. Miskulin 2

3. f(x) - f(a)
lim
x-a
x→a
m
3

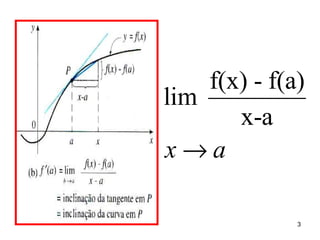
4. RETA TANGENTE À
CURVA
y = f (x), no ponto
P ( a, f (a) ), pode ser
considerada como sendo a
reta que passa por P e
possui inclinação m
m= lim [f ( a + h) - f(a)] /h
h 0
Pela definição de Derivada:
f ’ (a) = lim [f ( a + h) - f(a) ]/h
h 0
4

5. EXEMPLO: ENCONTRE A DERIVADA DA FUNÇÃO:
f (x) = x2 - 8x + 9, NO PONTO P(a, f(a))
Pela definição:
f ’ (a) = lim [f ( a + h) - f(a) ]/h =
h 0
x = a + h, então:
lim[ ( a + h )2 – 8 ( a + h ) + 9 – ( a2 -8a + 9 ) ]/ h =
Lim [a2 + 2ah + h2 – 8a - 8h + 9 – a2 + 8a -9 ] /h
Lim [2ah + h2 – 8h ]/ h = lim [h( 2a + h – 8)] /h =
5

6. PELA DEFINIÇÃO DE DERIVADA TEMOS QUE:
f’(x)=
f(x) - f(a)
lim
x-a
x→a
EXEMPLO: ENCONTRE A DERIVADA DA FUNÇÃO:
f (x) = x2 - 8x + 9, NO PONTO P(a, f(a))
6

7. f(x) - f(a)
lim , sendo f (x) = x 2 - 8x + 9, NO PONTO P(a, f(a))
x-a
x→a
x 2 - 8x + 9 - (a 2 -8a+9) x 2 - 8x + 9 - a 2 +8a-9
f '(x) = lim = lim =
x-a x-a
x→a
x 2 - a 2 - 8x +8a + 9 -9 (x+a)(x-a) - 8x +8a
lim = lim
x-a x-a
(x+a)(x-a) - 8(x -a) (x-a)[(x+a) - 8]
= lim = lim = lim [(x+a) - 8] = 2a − 8
x-a (x-a)
x→a x→a x→a
Resp: 2a-8
7

8. EXEMPLO: ENCONTRE A DERIVADA DA FUNÇÃO:
f (x) = x2 - 8x + 9, NO PONTO P(a, f(a))
f (x) = x2 - 8x + 9, no ponto P(a, f(a))
f ’(x) = 2x - 8 , no ponto P(a, f(a))
f ’(x) = 2a- 8
8

9. EXEMPLO 2
ENCONTRE A EQUAÇÃO DA RETA tangente à
PARÁBOLA y = x2 – 8x + 9, no ponto P (3, -6).
Como no ex. anterior, a derivada da função f , no ponto a é
f ’ (a) = m = lim f ( a + h) - f(a) /h = 2a-8
h 0
PORTANTO, A INCLINAÇÃO DA RETA TANGENTE EM (3, -6 )
É: f ’ (x) = f’ (3) = 2 . 3 – 8 = 6 – 8 = m=-2
PORTANTO, A EQUAÇÃO DA RETA TANGENTE É:
y – f (a) = f’ (a) . (x – a)
No ponto (3, -6)
y – (-6) = f ’ (a) (x –a)
y +6 = -2 (x – 3) = y + 6 = -2x +6  y = -2x 9

10. 10

11. INTERPRETAÇÃO DA DERIVADA
COMO A TAXA INSTANTANEA de
VARIAÇÃO
EXEMPLO: Para uma motocicleta viajando a
uma velocidade v milhas /h quando é freada,
a distância d (em pés) necessária para parar
a motocicleta pode ser aproximada da
fórmula
d = 0,05v2 + v .
Encontre a taxa de variação instantânea da
distância em relação à velocidade, quando a
velocidade for 49 milhas/h.
Profa. Rosana G. S. Miskulin 11

12. Resolução:
d = 0,05v2 +v
a taxa de variação
instantânea da distância em
relação à velocidade =
derivada =
d’= 2. (0,05) v +1 =
= 0,10. 49 + 1 = 5,9 milhas/h
12