O documento descreve como Fermat e Newton, de forma independente, chegaram ao conceito de derivada ao tentarem resolver problemas diferentes: Fermat sobre tangentes a curvas e Newton sobre velocidade instantânea. A derivada representa a taxa de variação de uma função num determinado ponto e foi fundamental para o desenvolvimento do cálculo diferencial.

1. Na Rota da DerivadaTaxa Média de Variação e Taxa de Variação

2. Pierre de Fermat (1601-1665) chegou ao conceito de derivadana resolução de um problemarelacionado com tangentes a curvas.O corpo de raio r roda sobre a curva C’ e a curva C descreve a trajectória do centro do corpo.O ângulo θ mede a inclinação da recta tangente a curva C’ em P. Isaac Newton (1642-1727) chegou ao conceito de derivadana determinação davelocidade instantânea.

3. 1. Nota HistóricaFermat e Newton, com o objectivo de resolverem dois problemas diferentes, chegaram um dos mais importantes conceitos da matemática: o conceito de Derivada. Fermat colocou a questão:“Como determinar o declive de uma recta tangente a uma curva?”A recta a tem com a curva dois pontos comuns e é tangente à curva.A recta c tem com a curva um só ponto comum e não é tangente à curva.Como definir então a tangente a uma curva?

4. Fermat pretendia determinar o declive de uma recta tangente a um ponto qualquer de uma curva. Para isso, considerou um ponto P de uma curva e uma secante PQ. Concluiu que o declive da recta tangente à curvapodia ser calculado como o limite do declive da secante PQquando o ponto Q, percorrendo a curva, se aproxima de P (Q1, Q2, Q3,…)Se P é um ponto fixo e que um ponto se aproxima de Pocupando as posições sucessivas Q1, Q2, Q3,…, as secantes terão as posições dadas por PQ1, PQ2, PQ3,… e os declives dessas rectas secantes ficarão cada vez mais próximas do declive da recta tangente. .

5. Newton pretendia determinar a velocidade instantânea, ou seja, a velocidade dada pelo velocímetro de um automóvel em movimento, conhecendo apenas a relação entre o espaço e o tempo.Para determinar a velocidade instantânea no momento a , Newton considerou um intervalo de tempo em que a era um extremo, por exemplo: [a , a + h]Calculou a velocidade média nesse intervalo; Reduzindo sucessivamente h , calculou de novo a velocidade média para cada um dos intervalos. Concluiu então que podia determinar a velocidade instantânea em a através do limite da velocidade média no intervalo[a , a + h] quando h  0

6. Nas situações apresentadas, aparece a referência a um limite:o declive da recta tangente a uma curva é um limite;a velocidade instantânea é um limite. ** Hoje, a estes limites chamamos derivadas.

7. 2. DERIVADA de uma FUNÇÃO NUM PONTO como DECLIVE DE UMA RECTATaxa de variação média. Velocidade médiaImaginemos a situação seguinte:Ligou-se um computador ao velocímetro de um carro de Fórmula 1 durante um treino. O gráfico da função fobtido dá-nos a ideia de como variou a velocidade ao longo dos primeiros 25 segundos do movimento:

8. A taxa de variação média da função f no intervalo [a , b] é dada por:Fixemo-nos no intervalo [10 , 15] e calculemos a taxa de variação média neste intervalo:O número 20 também é o declive da recta PQ Este número 20 diz-nos que, em média, dos 10 aos 15 segundos a velocidade aumentou 20 km/h , por segundo. Se em média aumentou 20 não quer dizer que em cada segundo tenha aumentado 20 !

9. Taxa de variação. Velocidade instantâneaSuponhamos que queríamos saber quanto aumentou exactamente no 10º segundo. De acordo com Fermat, utilizando material de desenho, desenhamos com o rigor que nos for possível a recta tangente à curva no ponto P.Para obtermos a recta tangente à curva no ponto P fixamos o ponto P e, deslocando o ponto Q ao longo da curva, desenhamos algumas secantes para ajudar a obter, com o rigor que nos for possível, a recta t. À medida que o ponto Q se aproxima de P , o declive das sucessivas secantes aproxima-se do declive da recta tangente t.

10. Determinemos o declive da rectat utilizando dois dos seus pontos:A (6 , 0) e P (10 , 150) Concluímos que o aumento da velocidade no instante t = 10 s foi aproximadamente 37,5 kmh-1 / s Ao número 37,5 chamamos derivada da funçãono ponto de abcissa x = 10, outaxa de variação da função no ponto de abcissa x = 10.Escreve-se f’ (10) = 37,5A derivada da função no ponto x = 10 é o declive da recta tangente ao gráfico da função no ponto de abcissa x = 10

11. Geometricamente, a derivada de uma função no ponto de abcissa x0 é o declive da recta tangente ao gráfico da função no ponto de abcissa x0

12. 3. INTERPRETAÇÃO DA DERIVADA de uma FUNÇÃO NUM PONTO Considere-se a seguinte situação:Um objecto foi lançado na vertical de um ponto P e daí a alguns instantes caiu de novo no ponto P. A distância a da bola à origem é dada por:a(t) = 12t – 3t2 com t em segundos e a em metrosO gráfico que ilustra a situação é o seguinte:

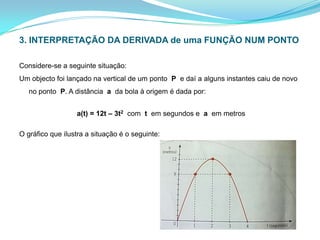
13. Calcule-se a taxa de variação média, que neste caso é a velocidade média, para os intervalos [0 , 1] ; [1 , 2] e [2 , 3]:t.v.m. [0 , 1] = t.v.m. [1 , 2] = t.v.m. [2 , 3] = Verificou-se que a velocidade média era positiva nos dois primeiros intervalos e negativa no outro. Significa isto que a bola mudou de sentido. Ia a subir e passou a descer.Verificou-se que t.v.m. [0 , 1] > t.v.m. [1, 2]o que significa que existe variação maior no intervalo [0 , 1] do que no intervalo [1 , 2], ou seja, que a velocidade média é maior no intervalo [0 , 1] do que no intervalo [1 , 2].

14. Qual será a derivada da função no ponto de abcissa 1 ? Ou seja, qual será a velocidade instantâneano instante t = 1 ? Ou seja, qual será a taxa de variaçãoda função no ponto de abcissa 1 ? Ou seja, qual será a’ (1)?Considere-se o intervalo [1 , 1+ h]e h  0 t.v.m. [1 ; 1,1] = t.v.m. [1 ; 1,01] = t.v.m. [1 ; 1,001] = À medida que htende para zero, a velocidade média parece tender para 6. Ou seja, a velocidade instantânea no instante t=1 parece ser 6 m/s , ou seja, f’(1) = 6

15. Um pouco mais de História A noção da derivada surgiu no séc. XVII marcado pela criação do cálculo diferencial ao qual estão ligados os nomes de dois grandes vultos da Ciência – Newton e Leibniz. Newton foi estimulado no seu trabalho pela necessidade de encontrar utensílios Matemáticos que dessem suporte à sua teoria da gravitação universal. Com efeito, no âmbito das suas investigações sobre mecânica celeste, Newton teve necessidade de resolver problemas sobre trajectórias de astros, velocidades, tangentes, máximos e mínimos. Por sua vez, Leibniz lançou também os fundamentos do Cálculo Infinitesimal (na mesma época que Newton mas independentemente dele), constituindo o seu trabalho um avanço decisivo na criação de uma linguagem comum a várias ciências e à filosofia. Foi com Newton e Leibniz que a Análise Infinitesimal se tornou um ramo da Matemática, autónoma em relação à Geometria.

16. Derivadas sempre na Matemática