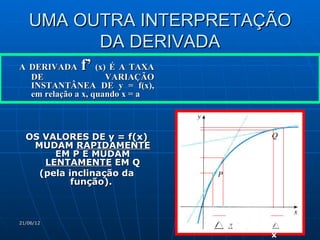
O documento discute conceitos fundamentais sobre derivadas, incluindo: (1) a derivada fornece informações sobre a taxa de variação instantânea de uma função; (2) a derivada de uma função f(x) no ponto x=a é definida como o limite da inclinação da reta tangente quando h tende a zero; (3) a derivada pode ser interpretada geometricamente como a inclinação da reta tangente ou algébricamente como uma função.

1. DERIVADAS
( Baseado em Stewart, J. – Cálculo I
 O LIMITE NOS DÁ INFORMAÇÕES PONTUAIS
SOBRE AS FUNÇÕES.
 ELE INDICA PARA ONDE TENDE A FUNÇÃO EM
UM PONTO NO QUAL ELA NÃO ESTÁ DEFINIDA ,
OU NOS FORNECE O VALOR DA FUNÇÃO EM UM
PONTO ONDE ELA ESTÁ DEFINIDA.
 A DERIVADA NOS FORNECE O
COMPORTAMENTO DA FUNÇÃO EM SEU
DOMÍNIO
21/06/12 1

2. DERIVADAS
A INCLINAÇÃO DA TANGENTE À CURVA
y = f (x), no ponto x = a, foi definida como
sendo:
m = lim f ( a + h ) – f (a ) / h
h 0
Seja s = f (t) a função posição de um objeto. A velocidade desse
objeto no instante t = a é:
v (a) = lim f (a + h) - f(a) /h
h 0
ESSE LIMITE SURGE SEMPRE AO CALCULARMOS TAXAS DE
VARIAÇÕES EM ÁREAS DIVERSAS DE CIÊNCIA E
ENGENHARIA.
QUANDO ESSE LIMITE OCORRE AMPLAMENTE DÁ-SE O
NOME DE DERIVADA.
21/06/12 2

3. DEFINIÇÃO - DERIVADA
 A DERIVADA DE UMA FUNÇÃO EM UM
NÚMERO a, DENOTADO POR
f’ (a) = lim f ( a + h) - f(a) /h, se o limite existe.
h 0
Forma equivalente como já foi visto,
anteriormente, no cálculo da reta tangente
pode ser escrito como:
( x = a + h e h = x -a) f’ (a) = lim f ( x) - f(a) /x - a
xa
21/06/12 3

4. EXEMPLO: ENCONTRE A DERIVADA DA FUNÇÃO:
f (x) = x2 - 8x + 9, NO PONTO P(a, f(a))
 Pela definição:
f’ (a) = lim f ( a + h) - f(a) /h =
h 0
x = a = h, então:
lim ( a + h )2 – 8 ( a + h ) + 9 – ( a2 -8a + 9 ) / h =
Lim a2 + 2ah + h2 – 8a - 8h + 9 – a2 + 8a -9 /h
Lim 2ah + h2 – 8h / h = lim ( 2a + h – 8) = 2a - 8
21/06/12 4

5. INTERPRETAÇÃO DA DERIVADA
COMO A INCLINAÇÃO DA RETA TANGENTE
RETA TANGENTE À CURVA y = f (x), no ponto
P ( a, f (a) ), pode ser considerada como sendo a reta
que passa por P e possui inclinação m
m = lim f( a + h) - f(a) /h
h 0
PELA DEFINIÇÃO DE DERIVADA TEMOS QUE:
f’ (a) = lim f (x) - f(a) /x – a
x a
= f’ (a) = lim f (a + h) - f(a) /h
h  0, se o limite existe.
21/06/12 5

6. INTERPRETAÇÃO GEOMÉTRICA
x
21/06/12 6

7. ESCREVER UMA EQUAÇÃO DA RETA TANGENTE À
CURVA y = f (x), NO PONTO P(a, f (a) )
EQUAÇÃO DA RETA TANGENTE À
CURVA :
y = f (x), no ponto P (a, f(a))
y – f (a) = f’ (a) . (x – a)
m
21/06/12 7

8. EXEMPLO 2 : ENCONTRE UMA EQUAÇÃO DA RETA À PARÁBOLA
Y = x2 – 8x + 9, no ponto P (3, -6).
Como no ex. anterior, a derivada da função f , no ponto a é
f’ (a) = lim f ( a + h) - f(a) /h = 2a-8
h 0
PORTANTO, A INCLINAÇÃO DA RETA TANGENTE EM (3, -6 )
É: f ’ (x) = f’ (3) = 2 . 3 – 8 = 6 – 8 = -2
PORTANTO, A EQUAÇÃO DA RETA TANGENTE É:
y – f (a) = f’ (a) . (x – a) .
No ponto (3, -6)
y – (-6) = f’ (a) (x –a)
y +6 = -2 (x – 3) = y + 6 = -2x +6  y = -2x
21/06/12 8

9. 21/06/12 9

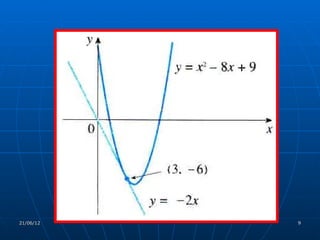
10. INTERPRETAÇÃO DA DERIVADA
COMO UMA TAXA DE VARIAÇÃO
FOI DEFINIDA ANTERIORMENTE A TAXA DE VARIAÇÃO
INSTANTÂNEA DE:
y = f(x) EM RELAÇÃO A x, EM x = x1, COMO
O LIMITE DAS TAXAS MÉDIAS DE VARIAÇÃO SOBRE
INTERVALOS CADA VEZ MENORES.
SE O INTERVALO FOR [ x1, x2 ], ENTÃO A VARIAÇÃO EM x É:
 x = x2 – x1 , A VARIAÇÃO CORRESPONDENTE EM y é:
 y = f(x2) – f(x1)
TAXA DE VARIAÇÃO INSTANTÂNEA
lim  y /  x = lim f(x2) – f( x1 ) / x2 – x1 =
 x 0 x2 x1
= derivada de f em x1 = f’ (x1)
21/06/12 10

11. UMA OUTRA INTERPRETAÇÃO
DA DERIVADA
A DERIVADA f’ (x) É A TAXA
DE VARIAÇÃO
INSTANTÂNEA DE y = f(x),
em relação a x, quando x = a
OS VALORES DE y = f(x)
MUDAM RAPIDAMENTE
EM P E MUDAM
LENTAMENTE EM Q
(pela inclinação da
função).
21/06/12
x  11
x

12. CURVA y = f(x)  TAXA INSTANTÂNEA DE
VARIAÇÃO  INCLINAÇÃO DA TANGENTE A
ESSA CURVA, NO PONTO x = a.
ISSO SIGNIFICA :
1-QUANDO A DERIVADA FOR GRANDE ( A CURVA
ESTÁ ÍNGRIME NO PONTO P)  OS VALORES DE
y MUDARÃO RAPIDAMENTE.
2- QUANDO A DERIVADA FOR PEQUENA ( A CURVA
SERÁ LEVEMENTE ACHATADA)  E OS VALORES
DE y MUDARÃO LENTAMENTE.
21/06/12 12

13. VELOCIDADE
Se S = f(t)  for a função posição de 1 partícula que
se move ao longo de uma reta, então:
f’ (a)  taxa de variação do deslocamento S em
relação ao tempo t.
f’ (a)  velocidade da partícula no instante t =a .
Rapidez da partícula  valor absoluto da velocidade
 l f’ (a) l , módulo da derivada de f em a.
21/06/12 13

14. EXEMPLO 4 P. 159
STEWART
A POSIÇÃO DE UMA PARTÍCULA É DADA PELA
EQUAÇÃO DO MOVIMENTO s = f (t) = 1 / (1 +t),
ONDE t é medido em segundos e s em metros.
Encontre a velocidade e a rapidez após 2 segundos.
Solução: A derivada de f em t é:
f’(t ) = f’(2) = lim f( t+h ) – f (t ) / h
h 0
Argumento é 2 +h, então: f’(2) = lim 1 / 1 + (2 +h) – 1 / 1 + 2
resolvendo, tem-se que: f’(t) = -1/9.
A velocidade após 2 segundos é – 1/9 e a rapidez que é o módulo
da velocidade é: mód. -1/9 = 1/9. m/s
21/06/12 14

15. A DERIVADA COMO UMA
FUNÇÃO
A DERIVADA DE UMA FUNÇÃO f EM UM
NÚMERO FIXO a:
f’ (a) = lim f (a + h ) – f(a) /h
h 0
VAMOS AGORA VARIAR O NÚMERO a
E SUBSTITUIR a por x
f’ (x) = lim f(x + h ) – f(x) /h
h 0
21/06/12 15

16.  Dado um número x, para o qual esse
limite existe  atribui-se a x o número f’
(x)
 f’ (x) = é uma nova função  chamada de
derivada de f, pois
tem sido derivada de f pela operação
limite na equação:
 f’ (x) = lim f(x + h ) – f(x) /h
h 0
O DOMÍNIO DE f’ (x) É O CONJ.
{ x / f’ (x) existe}
21/06/12 16