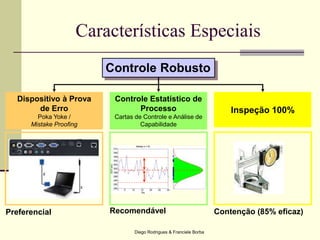
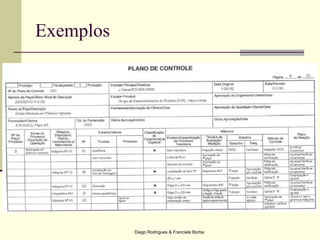
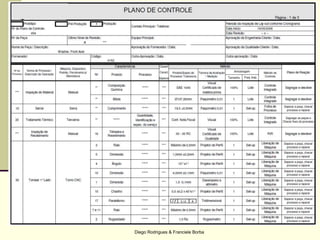
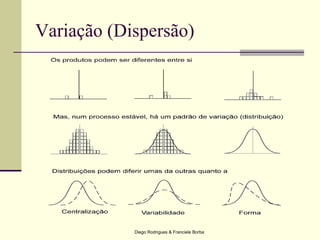
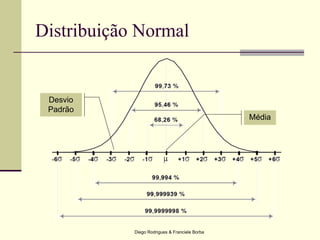
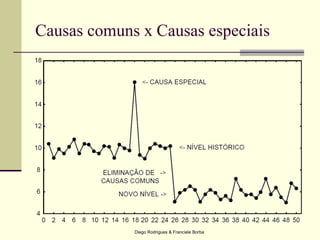
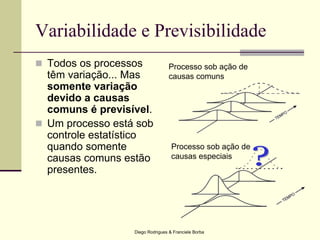
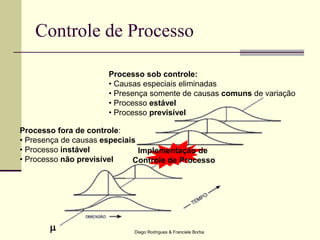
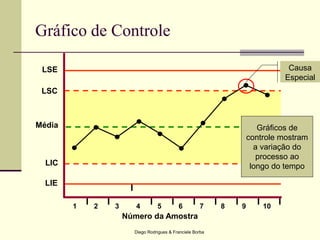
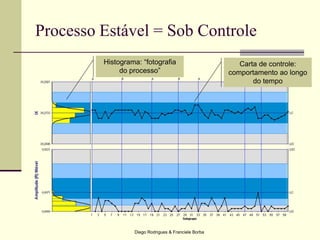
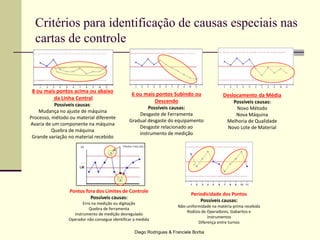
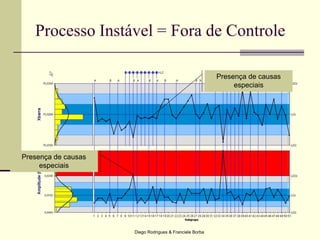
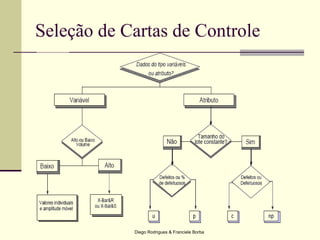
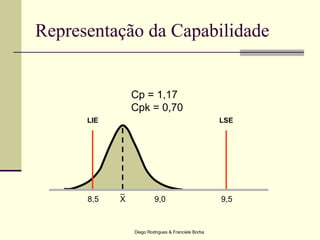
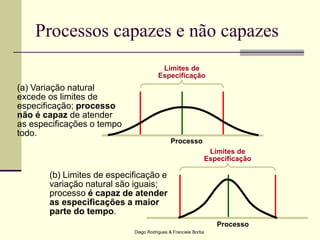
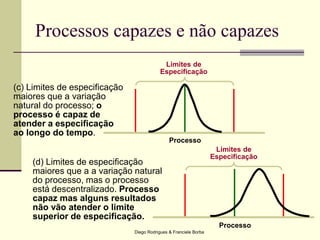
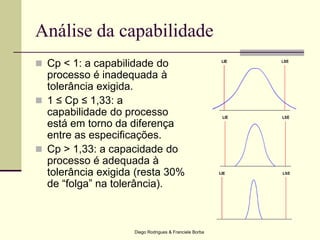
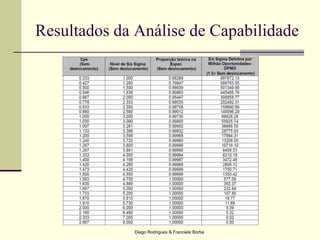
O documento apresenta os conceitos e técnicas de controle estatístico de processo, incluindo plano de controle, cartas de controle, análise de capabilidade de processo e índices como Cp e Cpk. É destacado que o objetivo é reduzir a variabilidade do processo através da identificação e eliminação de causas especiais de variação.