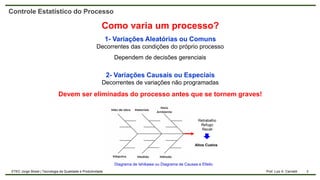
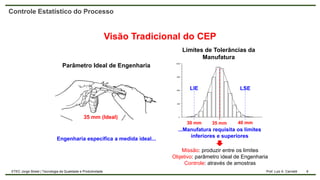
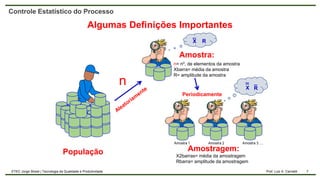
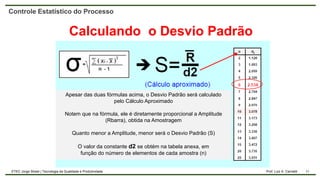
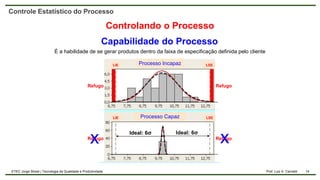
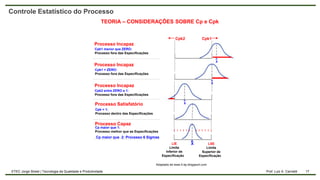
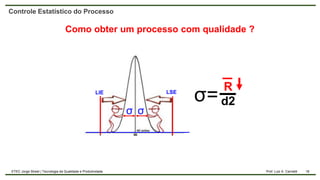
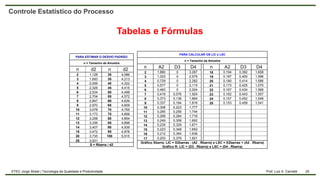
O documento aborda o controle estatístico do processo, enfatizando a importância de monitorar variações para garantir a qualidade na produção. Ele diferencia entre variações aleatórias e causais, discute a capabilidade do processo e apresenta métodos de cálculo como CP e CPK. Além disso, destaca a relevância de trabalhar com amostras para prevenir defeitos e melhorar a qualidade.