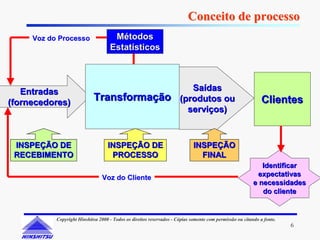
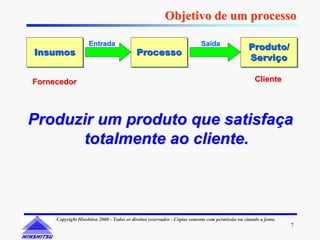
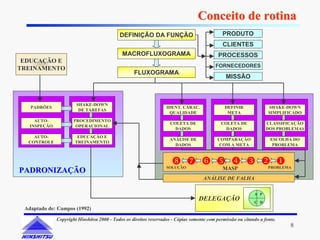
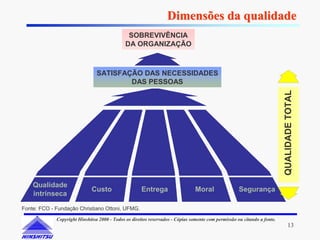
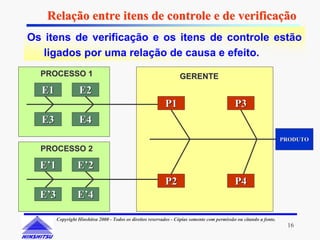
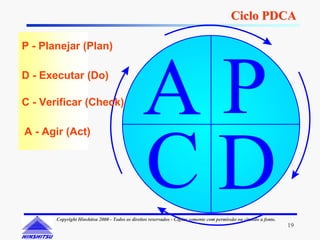
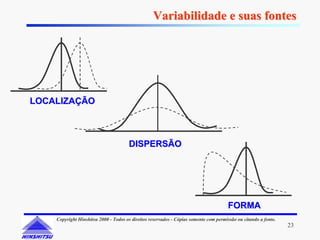
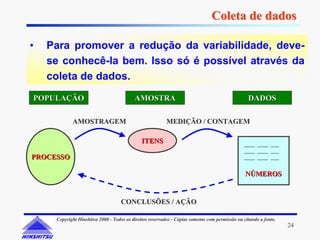
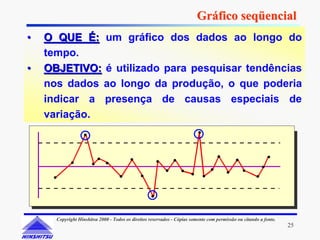
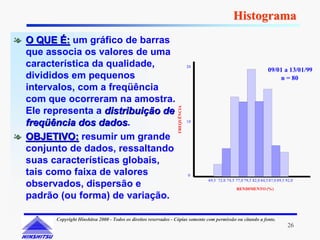
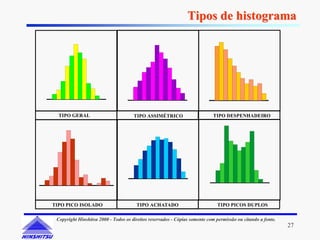
Este documento apresenta os conceitos e ferramentas do Controle Estatístico de Processos (CEP). Discute introdução a processos, gerenciamento de processos, avaliação de processos usando gráficos e índices de capacidade para melhorar processos produtivos.