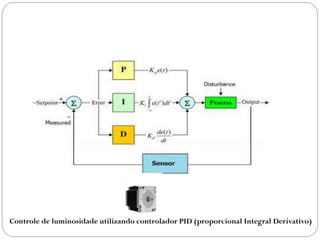
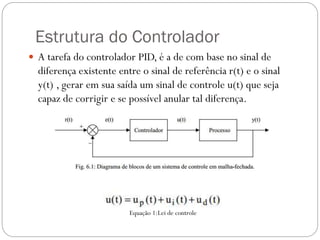
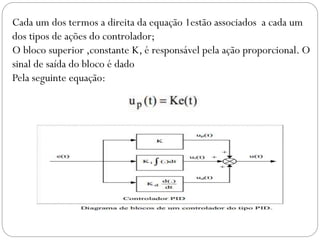
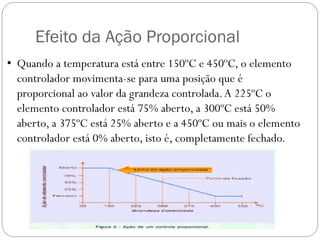
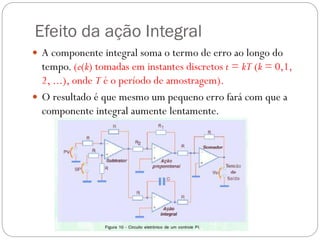
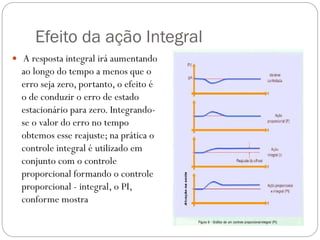
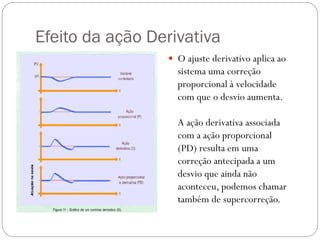
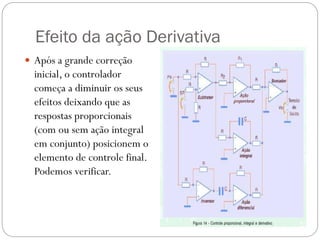
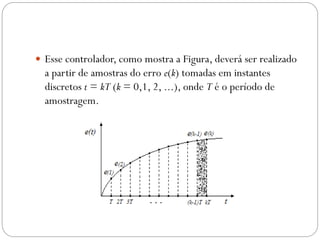
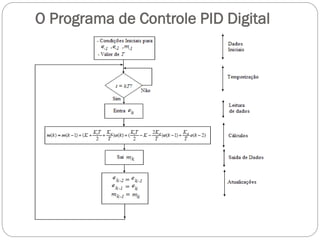
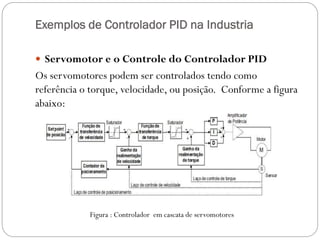
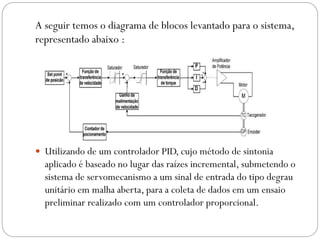
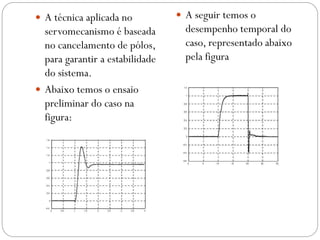
O documento descreve o funcionamento de controladores PID, incluindo suas ações proporcional, integral e derivativa. É explicado que o PID combina essas ações para minimizar o erro de processo de forma antecipada e precisa. Exemplos de aplicação de controladores PID em servomotores e outros sistemas industriais são apresentados.

1. Controlador PID
Paolla C. Normando
Isabela M. Bacelar
Elan Tarsis
Ticiane Cutrim

2. Conceito
 É uma técnica de controle de processos que une as ações derivativa,
integral e proporcional, fazendo assim com que o sinal de erro seja
minimizado pela ação proporcional, zerado pela ação integral e obtido
com uma velocidade antecipativa pela ação derivativa.
 É baseado na resposta da modelagem matemática de uma malha de
processo a ser controlada.
 Na prática os PID são encontrados no interior de controladores
eletrônicos chamados "single-loop", muitas vezes
com microprocessadores, e também através
de software em Controladores programáveis e outros equipamentos de
controle.
 A ideia básica por trás de um controlador PID é ler um sensor, calcular a
resposta de saída do atuador através do cálculo proporcional, integral e
derivativo e então somar os três componentes para calcular a saída

3. Controle de luminosidade utilizando controlador PID (proporcional Integral Derivativo)

4. Vantagens
Largamente utilizado na indústria devido à:
 Facilmente Implementável
 Baixo Custo
 Capacidade de alterar os comportamentos transitórios e de
regime permanente dos processos sob controle
Atualmente a maioria dos processos automatizados que utilizam
Controladores Lógicos Programáveis – CLP’s, possuem em
suas malhas de controle algoritmos PID.

5. Estrutura do Controlador
 A tarefa do controlador PID, é a de com base no sinal de
diferença existente entre o sinal de referência r(t) e o sinal
y(t) , gerar em sua saída um sinal de controle u(t) que seja
capaz de corrigir e se possível anular tal diferença.
Equação 1:Lei de controle

6. Cada um dos termos a direita da equação 1estão associados a cada um
dos tipos de ações do controlador;
O bloco superior ,constante K, é responsável pela ação proporcional. O
sinal de saída do bloco é dado
Pela seguinte equação:

7.  De modo análogo, pode se escrever os sinais de saída
relativos aos blocos integral e derivativo, apresentados nas
equações 3 e 4:
Equação 3
Equação 4

8. Efeito da Ação Proporcional
• Em processos que requerem um controle mais suave que aquele
fornecido pelo controlador ON-OFF, pode ser empregado o
controle proporcional (P).
O controle proporcional fornece uma relação linear fixa entre
o valor da variável controlada e o valor que o atuador de
controle pode fornecer

9. Efeito da Ação Proporcional
• Para ilustrar a ação de um controle proporcional. Usamos um
processo em que a temperatura de operação pode variar de
50ºC a 550ºC.
• O elemento controlador tem um raio de ação que fornece ao
processo uma faixa de temperatura que vai de 150ºC a 450ºC.
O ponto central é 300ºC com uma faixa de controle de
±150ºC. Quando a temperatura está em 150ºC ou menos, o
elemento controlador é todo aberto

10. Efeito da Ação Proporcional
• Quando a temperatura está entre 150ºC e 450ºC, o elemento
controlador movimenta-se para uma posição que é
proporcional ao valor da grandeza controlada. A 225ºC o
elemento controlador está 75% aberto, a 300ºC está 50%
aberto, a 375ºC está 25% aberto e a 450ºC ou mais o elemento
controlador está 0% aberto, isto é, completamente fechado.

11. Efeito da Ação Proporcional
• Com isso temos que a faixa de valores é de 300ºC, porém, esse
número expressa uma porcentagem da faixa total de excursão
da temperatura, que é de 500ºC (50ºC até 550ºC), portanto
temos que a faixa proporcional expressa 300ºC/500ºC, ou 60%
de todo o alcance da escala.

12. Efeito da Ação Proporcional
• Outra maneira de explicarmos o comportamento desse controlador é através do seu
Ganho, que é a relação entre a porcentagem de variação do elemento controlador pela
variação proporcional da grandeza. Assim temos:
Ganho = (% de variação do elemento controlador) / (% de variação da grandeza
controlada)
No nosso exemplo, o ganho seria de:
(100% no elemento controlador) / (60% de variação na grandeza) = 1,66.
Podemos dizer então, que:
Faixa proporcional = (100/Ganho)
% aberto, isto é, completamente fechado.

13. Efeito da Ação Proporcional
 No geral, aumentando o ganho proporcional irá aumentar a velocidade
da resposta do sistema de controle.
 No entanto, se o ganho proporcional é muito grande, a variável de
processo começará a oscilar.
 Se Kc(ganho proporcional) é aumentado ainda mais, as oscilações
ficarão maior e o sistema ficará instável e poderá oscilar até mesmo fora
de controle.

14. Efeito da ação Integral
 A componente integral soma o termo de erro ao longo do
tempo. (e(k) tomadas em instantes discretos t = kT (k = 0,1,
2, ...), onde T é o período de amostragem).
 O resultado é que mesmo um pequeno erro fará com que a
componente integral aumente lentamente.

15. Efeito da ação Integral
 A resposta integral irá aumentando
ao longo do tempo a menos que o
erro seja zero, portanto, o efeito é
o de conduzir o erro de estado
estacionário para zero. Integrandose o valor do erro no tempo
obtemos esse reajuste; na prática o
controle integral é utilizado em
conjunto com o controle
proporcional formando o controle
proporcional - integral, o PI,
conforme mostra

16. Efeito da ação Integral
 O Steady-State de erro é a diferença final entre as variáveis
do processo e do set point.
 Um fenômeno chamado windup integral ocorre quando a
ação integral satura um controlador, sem que o controlador
ajuste o sinal dê erro para zero. Este fato faz com que a malha
de realimentação seja de certa forma quebrada, pois o
atuador permanecerá no seu limite máximo (ou mínimo)
independentemente da saída do processo. Entretanto, se um
controlador com ação integral é utilizado, o erro continuará a
ser integrado e o termo integral tende a se tornar muito
grande, ou seja, tende a "carregar-se" demasiadamente

17. Efeito da ação Derivativa
 O ajuste derivativo aplica ao
sistema uma correção
proporcional à velocidade
com que o desvio aumenta.
A ação derivativa associada
com a ação proporcional
(PD) resulta em uma
correção antecipada a um
desvio que ainda não
aconteceu, podemos chamar
também de supercorreção.

18. Efeito da ação Derivativa
 Após a grande correção
inicial, o controlador
começa a diminuir os seus
efeitos deixando que as
respostas proporcionais
(com ou sem ação integral
em conjunto) posicionem o
elemento de controle final.
Podemos verificar.

19. Implementação
 Cada vez mais os controladores de processos são
implementados digitalmente por meio de
microcontroladores, DSPs, CLPs e computadores industriais.
Em todos esses casos, a ação de controle é realizada pela
execução de algumas linhas de programa presentes no
software do dispositivo.
 A ação de controle PID é dada por

20.  Esse controlador, como mostra a Figura, deverá ser realizado
a partir de amostras do erro e(k) tomadas em instantes
discretos t = kT (k = 0,1, 2, ...), onde T é o período de
amostragem.

21.  Ação Derivativa
A expressão 13 pode ser aproximada, a partir das amostras, por
 Ação Integrativa
A partir de (14), nos instantes de amostragem tem-se:

22.  O controlador PID Digital
A partir de (12), (15) e (17), chega-se ao Controlador PID
digital dado pela expressão iterativa

23. O Programa de Controle PID Digital

24. Exemplos de Controlador PID na Industria
 Servomotor e o Controle do Controlador PID
Os servomotores podem ser controlados tendo como
referência o torque, velocidade, ou posição. Conforme a figura
abaixo:
Figura : Controlador em cascata de servomotores

25.  A sequência começa com a posição, que será responsável por
gerar referência para a velocidade que por sua vez, gerará a
referência do torque. Cada bloco, posição, velocidade e
torque tem a sua própria realimentação, o que torna o
controle refinado e preciso, reduzindo atrasos em correção
 O sinal enviado ao servomotor ocorre pelo chaveamento dos
transistores comandados por modulação de largura de pulso
resultante dos cálculos do projeto do controlador.

27. A seguir temos o diagrama de blocos levantado para o sistema,
representado abaixo :
 Utilizando de um controlador PID, cujo método de sintonia
aplicado é baseado no lugar das raízes incremental, submetendo o
sistema de servomecanismo a um sinal de entrada do tipo degrau
unitário em malha aberta, para a coleta de dados em um ensaio
preliminar realizado com um controlador proporcional.

28.  A técnica aplicada no
servomecanismo é baseada
no cancelamento de pólos,
para garantir a estabilidade
do sistema.
 Abaixo temos o ensaio
preliminar do caso na
figura:
 A seguir temos o
desempenho temporal do
caso, representado abaixo
pela figura

29.  Com ambos os gráfico foi possível a partir dos mesmos,
comparar, como previsto, a resposta associada ao sinal de
referencia que é próxima a resposta do sistema de primeira
ordem que nesse caso, exibe uma maior velocidade de
reposta uma vez que o ganho proporcional associado ao PID
da realimentação é maior.