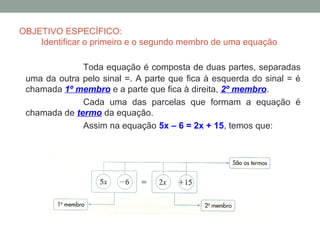
O documento discute expressões e sentenças matemáticas, classificando-as como abertas ou fechadas. Também define equações como sentenças matemáticas abertas expressas por uma igualdade, e explica que equações têm um primeiro e segundo membro. Por fim, discute reconhecer o número de variáveis em equações.

1. OBJETIVO ESPECÍFICO:
Reconhecer sentenças matemáticas abertas e fechadas.
EXPRESSÕES E SENTENÇAS MATEMÁTICAS
• “Lúcia .”
• “Oito menos três.”
• “Seis.”
Chama-se expressão o conjunto de palavras que
exprimem um pensamento incompleto.

2. OBJETIVO ESPECÍFICO:
Reconhecer sentenças matemáticas abertas e fechadas.
EXPRESSÕES E SENTENÇAS MATEMÁTICAS
• “Lúcia é minha amiga.”
• “Oito menos três é igual a cinco.”
• “Seis é menor que oito.”
• “Um número mais três é igual a dez.”
• “Um número menos dois é diferente de oito.”
Chama-se sentença o conjunto de palavras que
exprimem um pensamento completo.

3. OBJETIVO ESPECÍFICO:
Reconhecer sentenças matemáticas abertas e fechadas.
SENTENÇAS MATEMÁTICAS
• Oito menos três é igual a cinco. → 8 – 3 = 5
• Seis é menor que oito. → 6 < 8
• Um número mais três é igual a dez. → x + 3 = 10
• Um número menos dois é diferente de oito. → x – 2 ≠ 8

4. OBJETIVO ESPECÍFICO:
Reconhecer sentenças matemáticas abertas e fechadas.
As sentenças matemáticas podem ser
classificadas em verdadeiras ou falsas.
Exemplos:
8 – 3 = 5 (é uma sentença matemática verdadeira)
5 + 4 = 6 (é uma sentença matemática falsa)
x + 3 = 10 (é uma sentença matemática que pode ser
verdadeira ou falsa dependendo do valor atribuído a
x)

5. OBJETIVO ESPECÍFICO:
Reconhecer sentenças matemáticas abertas e fechadas.
As sentenças matemáticas podem ainda ser
classificadas em abertas ou fechadas.
1. Uma sentença matemática é fechada quando sua
classificação em verdadeira ou falsa não deixa dúvidas.
Exemplos:
8 – 3 = 5 (é uma sentença matemática fechada verdadeira)
6 < 8 (é uma sentença matemática fechada verdadeira)
5 + 4 = 6 (é uma sentença matemática fechada falsa)
8 - 3 = 9 (é uma sentença matemática fechada falsa)

6. OBJETIVO ESPECÍFICO:
Reconhecer sentenças matemáticas abertas e fechadas.
2. Uma sentença matemática é aberta
quando sua classificação em verdadeira ou falsa
deixa dúvidas.
Exemplos:
x + 3 = 10
x–2=8 São sentenças matemáticas abertas, pois sua
x+y=4
3x > 15
→ classificação em verdadeiras ou falsas
depende do valor que será colocado no lugar
das “letras”.

7. EXERCÍCIOS
1) Identifique: (E) expressão ou (S) sentença?
a) 8 + 4 = 12
b) 6 – 2 < 15
c) 3 . 7
d) 25 = 5
e) 6 – 3 ≠ 8
f) 4x
g) 3 + 2 . 5²
h) 3x = x + 5
i) x² + 5x + 6

8. EXERCÍCIOS
2) Identifique: (A) sentença aberta ou (F) sentença fechada?
a) 9 + 7 = 16
b) – 3 + y = 2
c) x – 4 = 12
d) x² = 16
e) 8 > 3
f) Z ⊂ Q
g) x + 4 < 20
h) 2x + 3y ≠ 0
i) 2 . ( 5 + 6 ) = 2 . 5 + 2 . 6

9. OBJETIVO ESPECÍFICO:
Identificar como equação toda sentença matemática aberta expressa por
uma igualdade.
EQUAÇÃO
Observe as seguintes sentenças matemáticas:
x – 15 = 23
5x – 6 = 2x + 15
x + y = 17
x² – 5x + 6 = 0
Todas elas representam sentenças matemáticas abertas
e expressam igualdade. São, por esse motivo, chamadas
de equações.

10. OBJETIVO ESPECÍFICO:
Identificar como equação toda sentença matemática aberta expressa por
uma igualdade.
Observe agora as seguintes sentenças matemáticas:
6.(5+4)=6.5+6.4
x – 4 < 12
x–9≠8
A primeira não representa uma sentença matemática
aberta e as demais são sentenças matemáticas abertas
que não expressam igualdade. Essas sentenças
matemáticas não representam equações.

11. OBJETIVO ESPECÍFICO:
Identificar como equação toda sentença matemática aberta expressa por
uma igualdade.
Definição de Equação
Equação é toda sentença matemática
aberta que expressa um igualdade.

12. OBJETIVO ESPECÍFICO:
Identificar o primeiro e o segundo membro de uma equação
Toda equação é composta de duas partes, separadas
uma da outra pelo sinal =. A parte que fica à esquerda do sinal = é
chamada 1º membro e a parte que fica à direita, 2º membro.
Cada uma das parcelas que formam a equação é
chamada de termo da equação.
Assim na equação 5x – 6 = 2x + 15, temos que:

13. OBJETIVO ESPECÍFICO:
Reconhecer o número de variáveis existentes numa equação.
Numa equação, as letras que nela aparecem e que
representam valores desconhecidos, recebem o nome de variáveis
ou incógnitas.
Exemplos:
5x – 4 = 16 → a variável é x.
2x + 5y = 26 → as variáveis são x e y.
x² – 5x + 6 = 0 → a variável é x.
a + b + c = 15 → as variáveis são a, b e c.

14. Importante!

15. EXERCÍCIOS
3) Identifique as sentenças abaixo que representam
equações.
a) 8 + 6 = 10 + 4
b) 6x + 3 = 4x + 10
c) 15 < 12 + 13
d) 5² +12 = 37
e) x + 2 = 17
f) x = - 13
g) x² ≠ 16
h) x + y + 6 = 18
i) 8 = 3 + 2x

16. EXERCÍCIOS
4) Indique o 1º membro e o 2º membro das seguintes equações.
a) 9x + 3 = 12
b) 18 = 4(x – 7)
c) x +12 = 3y – 4
d) x² – 7x + 12 = 0
1
e) 6 xy += 7x − 4
2
2
x 3 x 1
f) − = + 
5 2 2 4
 

17. EXERCÍCIOS
5) Identifique as variáveis de cada uma das seguintes equações
e os coeficientes de cada equação abaixo:
a) 5x - 18x = 7
b) 4y + 6 = 12y - 3
c) 2s + 3t = 5
d) 3pq = p + q
e) x ² - 5x + 6 = 0
b.c
f) = 12
2
k²
g) 3k - =6
5