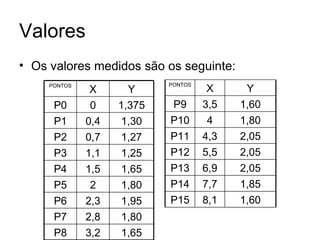
Este documento descreve o cálculo do volume de um frasco de leite fermentado usando interpolação de Lagrange. Fornece valores medidos de altura e raio em pontos ao longo do frasco e descreve os cálculos de interpolação realizados para aproximar a forma do frasco e calcular o volume total em aproximadamente 80 ml, com precisão de 0,8% em relação ao valor medido experimentalmente.

1. CENTRO DE CIÊNCIAS EXATAS E TECNOLÓGICAS ENGENHARIA ELÉTRICA Calculo Numérico CÁLCULO DE VOLUME POR INTERPOLAÇÃO AUGUSTO MAESTRO DANIEL A. DA SILVA DANILO E. MICHELIN LUCAS FAYMER LUIS GUSTAVO RAFAEL A. DE SOUZA WESLEI C. BARBOSA Londrina 2009

2. Conceito A interpolação de Lagrange permite fazer a reconstituição (aproximada) de uma função, apenas conhecendo algumas das suas abscissas e respectivas ordenadas. É um método que permite construir um novo conjunto de dados a partir de um conjunto discreto de dados pontuais conhecidos. Em engenharia e ciência, geralmente tem-se dados pontuais, obtidos a partir de uma amostragem ou experimento.

3. Conceito Através da interpolação pode-se construir uma função que aproximadamente encaixe-se nestes dados pontuais. Outra aplicação da interpolação e aproximação de funções complexas por funções mais simples. Suponha que tenhamos uma função, mas que seja muito complicada para avaliar de forma eficiente. Podemos então, escolher alguns dados pontuais da função complicada e tentar interpolar estes dados para construir uma função mais simples.

4. Interpolação de Lagrange Em análise numérica, polinômio de Lagrange (nomeado por razão de Joseph-Louis de Lagrange) é o polinômio de interpolação de um conjunto de pontos na forma de Lagrange Dado um conjunto de k +1 pontos: com todos xj distintos, o polinômio de interpolação de um conjunto de pontos na forma de Lagrange é a combinação linear dos polinômios da base de Lagrange:

5. Interpolação de Lagrange com polinômios da base de Lagrange dados por:

6. Objeto Para nosso trabalho, foi proposto calcular o volume de um frasco de leite fermentado, cujas formas aproximadas são as seguintes:

7. Valores Os valores medidos são os seguinte: P8 P7 P6 P5 P4 P3 P2 P1 P0 PONTOS 1,65 3,2 1,80 2,8 1,95 2,3 1,80 2 1,65 1,5 1,25 1,1 1,27 0,7 1,30 0,4 1,375 0 Y X Y X PONTOS 1,60 8,1 P15 1,85 7,7 P14 2,05 6,9 P13 2,05 5,5 P12 2,05 4,3 P11 1,80 4 P10 1,60 3,5 P9

8. Cálculos As interpolações foram as seguintes:

9. Cálculos

10. Cálculos

11. Cálculos

12. Cálculos

13. Cálculos

14. Soma dos valores parciais Somando-se os valores: 8,34+12,81+19,78+9,46+727,52+17,39= 795,3 unidades de volume Adequando o valor para mililitros temos 79,53 ml. O valor medido com uma balança e água destilada foi de 80,207 gramas, que equivalem a 80,207ml

15. Precisão Assim, conseguimos uma precisão de 0,8%