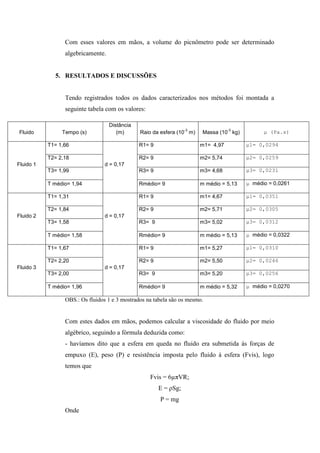
Este relatório descreve um experimento para determinar a viscosidade de dois fluidos usando um viscosímetro de Stokes. Mediu-se o tempo de queda de esferas em amostras dos fluidos dentro de um tubo vertical. Usando as medições de tempo, massa e diâmetro das esferas, calculou-se a viscosidade dos fluidos. Os resultados experimentais foram comparados com valores de literatura e as diferenças atribuídas à variação de temperatura entre os experimentos.

1. Universidade Federal do Triângulo Mineiro
Instituto de Ciências Tecnológicas e Exatas
Cursos de Engenharia
Viscosímetro de Stokes
Aluno: Fausto Pagan
Disciplina: Fundamentos de Fenômenos de Transporte.
Professor: Rúbner Gonçalves.
Uberaba-MG

2. 1. OBJETIVO
A aula experimental teve como objetivo a determinação da densidade absoluta
(µ) de um fluido a partir da descida de uma esfera nesse mesmo fluido, contido
em um tubo de vidro vertical.
2. INTRODUÇÃO
A viscosidade é uma característica completamente ligada aos fluidos.
Basicamente, viscosidade é a propriedade que os fluidos possuem em resistir ao
escoamento, dado certa temperatura.
Gases e líquidos , quando submetidos a tensões apresentam sua capacidade de
escoar, mostrando assim sua característica viscosa, diferentemente dos sólidos
que quando submetidos a tensões se deformam.
A viscosidade de um fluido pode ser determinada de diferentes formas, uma
delas é pelo Viscosímetro de Stokes, forma abordada na realização do
experimento que se baseia na velocidade e tempo de queda de uma esfera em um
determinado fluido.
O viscosímetro de Stokes, é um tubo de vidro contendo o líquido que desejamos
determinar sua viscosidade.
Nesse tubo, marca-se uma altura pré-determinada, e deixa-se cair uma esfera, de
diâmetro conhecido, no interior do fluido. Tendo a distância percorrida pela
esfera e seu tempo de queda, é possível determinar sua velocidade.
Enquanto a esfera cai pelo fluido ele é submetida ás forças de empuxo (E), peso
(P) e resistência imposta pelo fluido à esfera (Fvis).
Tendo em consideração esses conceitos pode-se então determinar a viscosidade
absoluta de um fluido, na qual discorremos no decorrer deste relatório.

3. 3. MATERIAIS
Esferas de vidro,
Proveta de vidro graduada;
Cronômetro;
Régua;
Picnômetro;
Balança;
Fluido 1: VR EXTRA MOLD SAE-40 API SF – VECCHI LUBRIFICANTES;
Fluido 2: MOBIL SUPER 1000 – API SM – 20W-50;
4. MÉTODOS
Mediu-se a massa das esferas de vidro e uma balança semi-analítica e anotaram-
se os respectivos valores;
Posteriormente, mediu-se o diâmetro da esfera, com auxílio de uma régua
milimétrica, adotando o mesmo valor de diâmetro para as demais esferas;
Em seguida, marcou-se uma altura de 17 cm na proveta de vidro, distância esta
que foi a percorrida pela esfera na descida.
Com auxílio de um cronômetro, o tempo de queda das esferas foi aferido e
anotado.
O mesmo foi feito para as demais esferas, sendo 3 esferas para um determinado
fluido e outras 6 esferas para outro. Nas provetas 1 e 3 foi colocado um fluido e
na proveta 2 foi colocado o segundo fluido.
Posteriormente 3 picnômetros foram pesados vazios, e em seguida pesados com
água, tendo seus respectivos valores anotados.
Em seguida, os picnômetros foram lavados e secos, sendo posteriormente
preenchidos com os fluidos em questão. E então foram novamente pesados.

4. Com esses valores em mãos, a volume do picnômetro pode ser determinado
algebricamente.
5. RESULTADOS E DISCUSSÕES
Tendo registrados todos os dados caracterizados nos métodos foi montada a
seguinte tabela com os valores:
Distância
-3 -3
Fluido Tempo (s) (m) Raio da esfera (10 m) Massa (10 kg) μ (Pa.s)
T1= 1,66 R1= 9 m1= 4,97 μ1= 0,0294
T2= 2,18 R2= 9 m2= 5,74 μ2= 0,0259
Fluido 1 d = 0,17
T3= 1,99 R3= 9 m3= 4,68 μ3= 0,0231
T médio= 1,94 Rmédio= 9 m médio = 5,13 μ médio = 0,0261
T1= 1,31 R1= 9 m1= 4,67 μ1= 0,0351
T2= 1,84 R2= 9 m2= 5,71 μ2= 0,0305
Fluido 2 d = 0,17
T3= 1,58 R3= 9 m3= 5,02 μ3= 0,0312
T médio= 1,58 Rmédio= 9 m médio = 5,13 μ médio = 0,0322
T1= 1,67 R1= 9 m1= 5,27 μ1= 0,0310
T2= 2,20 R2= 9 m2= 5,50 μ2= 0,0246
Fluido 3 d = 0,17
T3= 2,00 R3= 9 m3= 5,20 μ3= 0,0256
T médio= 1,96 Rmédio= 9 m médio = 5,32 μ médio = 0,0270
OBS.: Os fluidos 1 e 3 mostrados na tabela são os mesmo.
Com estes dados em mãos, podemos calcular a viscosidade do fluido por meio
algébrico, seguindo a fórmula deduzida como:
- havíamos dito que a esfera em queda no fluido era submetida ás forças de
empuxo (E), peso (P) e resistência imposta pelo fluido à esfera (Fvis), logo
temos que
Fvis = 6µπVR;
E = ρSg;
P = mg
Onde

5. µ = viscosidade absoluta do fluido;
V = velocidade da esfera;
R = raio da esfera;
ρ = massa específica do líquido;
Nas condições do equilíbrio dinâmico, temos que
P  E  Fvisc
4
mg   R 3 g  6VR
3
Pela fórmula acima, podemos isolar a viscosidade absoluta, resultando em:
4
mg   R 3 g
 3
6VR
Fórmula, que nos fornece algebricamente o valor da viscosidade do fluido em questão.
Os valores de viscosidade foram então calculados e dispostos na tabela apresentada
anteriormente.
Os valores encontrados na literatura para as massas específicas dos fluidos 1 e 2
são:
Fluido 1: ρ = 0,869 g/cm³
Fluido 2: ρ = 0,874 g/cm³
E os valores de viscosidade cinemática para os fluidos 1 e 2, também
encontrados na literatura são:
Fluido 1: mínimo 12,5 cSt = 12,5 cm²/s e máximo 16,3 cSt = 16,3 cm²/s para
uma temperatura de 100°C. Tomamos 14,4 cm²/s como sendo seu valor médio
de viscosidade cinemática.
Fluido 2: mínimo 146 cSt = 146 cm²/s e máximo 17,8 cSt = 17,8 cm²/s para uma
temperatura de 100°C. Tomamos 81,9 cm²/s como sendo o valor médio da
viscosidade cinemática.
Relacionando a viscosidade dinâmica com a cinemática temos que:
µ = ρν

6. Com,
µ = viscosidade dinâmica ou absoluta;
ρ = massa específica do fluido;
ν = viscosidade cinemática.
Pela fórmula apresentada obtivemos os seguintes valores de viscosidade
absoluta:
Fluido 1 = 1,251 Pa.s
Fluido 2 = 7,158 Pa.s
Da tabela, podemos observar que temos a viscosidade do fluido 1 como sendo
0,0261 Pa.s e do fluido 2 como sendo 0,0296 Pa.s. Equiparando os valores de
viscosidade encontrados na literatura, observamos relevada diferença entre os
valores. Sendo assim, podemos assumir essa diferença entre os valores como
sendo resultado da diferença de temperatura em que foram especificadas as
viscosidades, já que pela literatura as viscosidades foram fornecidas a uma
temperatura de 100°C enquanto o valor determinado pelo experimento foi
determinado à temperatura ambiente de 27°C.
Logo podemos registrar a influência que a temperatura exerce sobre a
viscosidade, como exemplo, citamos a dilatação que o fluido pode vir a sofrer, o
que alteraria o valor de sua viscosidade.
6. CONCLUSÃO
Pelo discutido, podemos concluir que o a diferença entre os valores de
viscosidade determinados experimentalmente e os encontrados na literatura se
devem ao fato das temperaturas não serem coincidentes.
O que era de se esperar, sabendo sobre a influência da temperatura sobre a
viscosidade, logo os valores encontrados experimentalmente são de válidos
quanto a temperatura em que se realizou o experimento (27°C).

7. 7. REFERÊNCIAS
ROTEIRO AULA PRÁTICA: viscosímetro de Stokes.
MOBIL SUPER 1000 20W-50, Rio de Janeiro – RJ – Brasil, 2009.
DIÁRIO OFICIAL DA UNIÃO de 27/11/2008, pág. 106, Seção 1, disponível
em http://www.jusbrasil.com.br/diarios/905133/dou-secao-1-27-11-2008-pg-
106. Acesso em: 30 de janeiro de 2013.