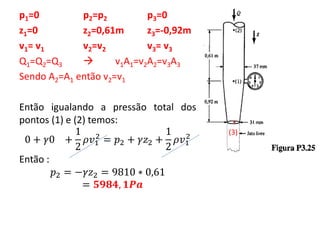
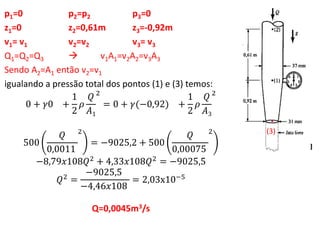
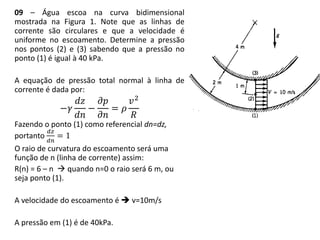
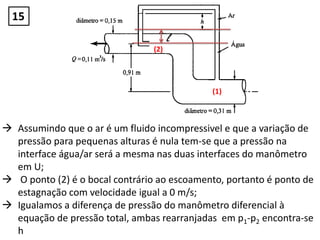
(1) A máxima pressão que atua na mão de uma pessoa fora de um automóvel a 105 km/h é de 520,1Pa. (2) A velocidade máxima do escoamento na torneira do subsolo é de 10,3m/s e a água não chega na torneira do primeiro andar. (3) A pressão no ponto 2 é de 5984,1Pa e a vazão é de 0,0045m3/s.

1. Solução Lista 2
2/2015

2. 01 – Uma pessoa coloca a mão para fora de um automóvel que
se desloca com uma velocidade de 105 km/h (29,2m/s) numa
atmosfera estagnada. Qual é a máxima pressão que atua na mão
exposta ao escoamento?
Usando (1) para pressão em um ponto a montante da mão
da pessoa e o ponto (2) para um ponto sobre a mão, sendo
a linha de corrente horizontal aplica-se a Equação de
Bernoulli:
𝑝1 + 𝛾𝑧1 +
1
2
𝜌𝑣1
2
= 𝑝2 + 𝛾𝑧2 +
1
2
𝜌𝑣2
2
Sendo p1 a pressão atmosférica a montante, portanto
usando pressão relativa p1=0; z1=z2; e v2=0, pois o ar se
choca com a mão gerando aumento de pressão tem-se:
1
2
𝜌𝑣1
2
= 𝑝2  𝑝2 =
1
2
∗ 1,22 ∗ 29,2 2
= 520,1𝑃𝑎

3. 02 – Água escoa na torneira localizada no
andar térreo do edifício mostrado na Figura 2
com velocidade máxima de 6,1 m/s.
Determine as velocidades máximas dos
escoamentos nas torneiras localizadas no
subsolo e no primeiro andar do edifício.
Admita que o escoamento é invíscido e que a
altura de cada andar seja igual a 3,6m.
A água escoa como jato livre portanto nas
saídas e no nível do reservatório a pressão é a
atmosférica.
Aplicando a Equação de pressão total
exatamente nos bocais de cada torneira, tem-
se:
p1=p2=p3
z1=0 z2=3,6m z3=7,2m
v1= v1 v2=6,1m/s v3= v3
𝑝1 + 𝛾𝑧1 +
1
2
𝜌𝑣1
2
= 𝑝2 + 𝛾𝑧2 +
1
2
𝜌𝑣2
2
= 𝑝3 + 𝛾𝑧3 +
1
2
𝜌𝑣3
2
(3)
(2)
(1)
1
2
𝜌𝑣1
2
= 𝛾𝑧2 +
1
2
𝜌𝑣2
2
= 𝛾𝑧3 +
1
2
𝜌𝑣3
2

4. Igualando a pressão do ponto 1 ao ponto 2:
1
2
𝜌𝑣1
2
= 𝛾𝑧2 +
1
2
𝜌𝑣2
2
500𝑣1
2
= 9810 ∗ 3,6 + 500 ∗ 6,02
𝒗 𝟏 =
35316 + 18000
500
= 𝟏𝟎, 𝟑𝒎/𝒔
Igualando a pressão do ponto 3 ao ponto 2:
𝛾𝑧2 +
1
2
𝜌𝑣2
2
= 𝛾𝑧3 +
1
2
𝜌𝑣3
2
𝑣3
2
=
9810 ∗ 3,6 + 500 ∗ 6,12 − 9810 ∗ 7,2
500
𝒗 𝟑
𝟐
=
35316 + 18000 − 70632
500
= −𝟑𝟒, 𝟔 (água não chega na 3ª torneira, quando todas estão abertas)

5. 03 – Água escoa em regime permanente na
tubulação mostrada na Figura 4. Sabendo que o
manômetro indica a pressão relativa nula no ponto
1 e admitindo que os efeitos viscosos são
desprezíveis, determine a pressão no ponto 2 e a
vazão em volume neste escoamento.
Aplicando a Eq de pressão total ao
escoamento e o bocal sendo jato livre
temos:
p1=0 p2=p2 p3=0
z1=0 z2=0,61m z3=-0,92m
v1= v1 v2=v2 v3= v3
Q1=Q2=Q3  v1A1=v2A2=v3A3
Sendo A2=A1 então v2=v1
.
(3)
𝑝1 + 𝛾𝑧1 +
1
2
𝜌𝑣1
2
= 𝑝2 + 𝛾𝑧2 +
1
2
𝜌𝑣2
2
= 𝑝3 + 𝛾𝑧3 +
1
2
𝜌𝑣3
2

6. p1=0 p2=p2 p3=0
z1=0 z2=0,61m z3=-0,92m
v1= v1 v2=v2 v3= v3
Q1=Q2=Q3  v1A1=v2A2=v3A3
Sendo A2=A1 então v2=v1
Então igualando a pressão total dos
pontos (1) e (2) temos:
0 + 𝛾0 +
1
2
𝜌𝑣1
2
= 𝑝2 + 𝛾𝑧2 +
1
2
𝜌𝑣1
2
Então :
𝑝2 = −𝛾𝑧2 = 9810 ∗ 0,61
= 𝟓𝟗𝟖𝟒, 𝟏𝑷𝒂
.
(3)

7. p1=0 p2=p2 p3=0
z1=0 z2=0,61m z3=-0,92m
v1= v1 v2=v2 v3= v3
Q1=Q2=Q3  v1A1=v2A2=v3A3
Sendo A2=A1 então v2=v1
igualando a pressão total dos pontos (1) e (3) temos:
0 + 𝛾0 +
1
2
𝜌
𝑄
𝐴1
2
= 0 + 𝛾(−0,92) +
1
2
𝜌
𝑄
𝐴3
2
500
𝑄
0,0011
2
= −9025,2 + 500
𝑄
0,00075
2
−8,79𝑥108𝑄2 + 4,33𝑥108𝑄2 = −9025,5
𝑄2
=
−9025,5
−4,46𝑥108
= 2,03x10−5
Q=0,0045m3/s
.
(3)

8. 04 – Água escoa na concentração
axisimétrica mostrada na Figura P3.30.
Determine a vazão em volume na
contração em função de D sabendo que a
diferença de alturas no manômetro é
constante e igual a 0,2 m.
Aplicando a Eq. Bernoulli aos pontos (1) e (2):
𝑝1 + 𝛾𝑧1 +
1
2
𝜌𝑣1
2
= 𝑝2 + 𝛾𝑧2 +
1
2
𝜌𝑣2
2
Tem-se que:
Z1=Z2
p1-p2=Δh*(ϒágua-ϒar)  diferença de pressão do manômetro diferencial
Q1=v1A1 Q2=v2A2 v2=Q/A2 v1=Q/A1
∆𝑕 𝛾 𝑎𝑔𝑢𝑎 − 𝛾 𝑎𝑟 + 500(02) = 500
𝑄2
𝐴2
2
RESOLVER
(1) (2)

9. 05 – Água escoa em regime
permanente na tubulação
mostrada na Figura P3.48.
Alguns experimentos revelaram
que o trecho de tubulação com
parede fina (diâmetro interno
=m 100 mm) colapsa quando a
pressão interna se torna igual a
externa menos 10 kPa. Até que o
valor de h a tubulação opera
convenientemente?
Comportamento de jato livre
A pressão total aos pontos 1, 2 e 3 será:
𝑝1 + 𝛾𝑧1 +
1
2
𝜌𝑣1
2
= 𝑝2 + 𝛾𝑧2 +
1
2
𝜌𝑣2
2
= 𝑝3 + 𝛾𝑧3 +
1
2
𝜌𝑣3
2
p1=0 p2=-10x103Pa p3=0
z1=1,22m z2=0 z3=-h
v1= 0 v2=v2 v3= v3
(1)
°
(2)
°
(3)
°

10. Comportamento de jato livre
A pressão total aos pontos 1, 2 e 3 será:
𝑝1 + 𝛾𝑧1 +
1
2
𝜌𝑣1
2
= 𝑝2 + 𝛾𝑧2 +
1
2
𝜌𝑣2
2
= 𝑝3 + 𝛾𝑧3 +
1
2
𝜌𝑣3
2
p1=0 p2=-10x103Pa p3=0
z1=1,22m z2=0 z3=-h
v1= 0 v2=v2 v3= v3
Assim:
0 + 9810 ∗ 1,22 +
1
2
𝜌02 = −10000 + 𝛾0 +
1
2
1000 ∗ 𝑣2
2
9810 ∗ 1,22 + 10000
500
= 𝑣2
2
𝑣2 = 6,6𝑚/𝑠
v2A2=v3A3  v3=v2A2/A3 Igualando as pressões totais do ponto 3 ao ponto 2 tem-
se:
−10000 +
1
2
1000 ∗ 6,62
= 0 + 9810(−𝑕) +
1
2
1000 6,6 ∗
0,12
0,1522
2
h=0,78m o negativo se deve ao referencial z2=0m

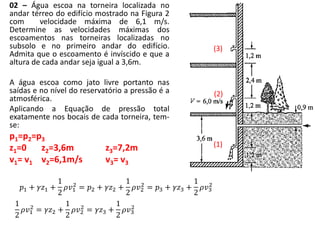
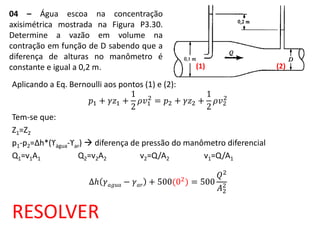
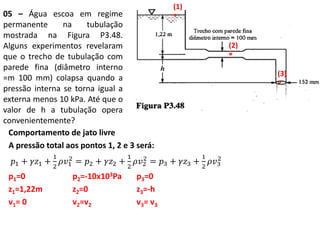
11. 06 – A vazão de água que é bombeada de um lago, através de
uma tubulação com 0,2 m de diâmetro, é 0,28 m3/s. Qual é a
pressão no tubo de sucção da bomba numa altura de 1,82 m
acima da superfície livre do lago? Admita que os efeitos viscosos
sejam desprezíveis.
Q=0,28m3/s
D=0,2m
p2 .
h= 1,82m
p1
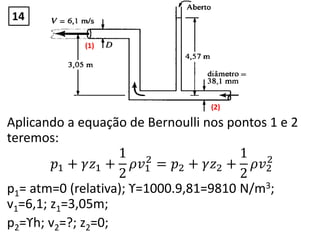
Aplicando a equação de pressão total ao longo da
linha de corrente da superfície do lago/bocal do
tubo até a altura de 1,82m tem-se:
𝑝1 + 𝛾𝑧1 +
1
2
𝜌𝑣1
2
= 𝑝2 + 𝛾𝑧2 +
1
2
𝜌𝑣2
2
Onde: p1= 0 (atmosfera/relativa) ; z1= 0; v1=0
p2= ?; z2=1,82m
v2=Q/A  v2=0,28/{[3,14*(0,2^2)]/4}=8,91m/s
Então:
0 + 𝛾0 +
1
2
𝜌02
= 𝑝2 + 𝛾1,82 +
1
2
𝜌8,912
p2= -(9810*1,82)-(500*(8,91^2))= -57,5kPa

12. 07 – A velocidade e o gradiente de pressão no ponto A de um escoamento de ar
são iguais a 20 m/s e 100 N/m3. Estime a velocidade do escoamento no ponto B
que pertence à mesma linha de corrente e que está localizado a 0,5 m à jusante
do ponto A.
A equação de movimento de um partícula fluida ao longo da linha de corrente é:
−𝛾𝑠𝑒𝑛𝜃 −
𝑑𝑝
𝑑𝑠
= 𝜌𝑣
𝑑𝑣
𝑑𝑠
Sendo:
𝑑𝑝
𝑑𝑠
 o gradiente de pressão ao longo da linha de corrente
𝑣
𝑑𝑣
𝑑𝑠
 a aceleração da partícula fluida (as)
Assumindo que a o escoamento se dá em uma linha de corrente horizontal tem-
se que θ = 0
Então: −
𝑑𝑝
𝑑𝑠
= 𝜌𝑣
𝑑𝑣
𝑑𝑠
onde dv/ds será o gradiente de velocidade ao longo
da linha de corrente
𝑑𝑣
𝑑𝑠
= −
𝑑𝑝
𝑑𝑠
𝜌𝑣
= −
100
1,22 ∗ 20
= −4,1/𝑠

13. A variação de velocidade entre dois pontos do escoamento pode ser igualada
ao gradiente de velocidade e assim a diferença de velocidade será:
∆𝑣 =
𝑑𝑣
𝑑𝑠
∗ ∆𝑠 = (-4,1)*0,5 = - 2,05 m/s
A velocidade em um ponto a 0,5m é:
∆𝑣 = 𝑣𝑓 − 𝑣𝑖
𝑣𝑓 = 𝑣𝑖 + ∆𝑣
𝑣𝑓 = 20 + −2,05 = 18,05𝑚/𝑠
A velocidade tende a diminuir com diferencial de pressão positivo

14. 08 - Qual o gradiente de pressão ao longo da linha de corrente, dp/ds,
necessário para impor uma aceleração de 9,14 m/s2 no escoamento
ascendente de água num tubo vertical? Qual o valor deste gradiente se o
escoamento for descendente?
A equação de movimento de um partícula fluida ao longo da linha de corrente
é:
−𝛾𝑠𝑒𝑛𝜃 −
𝑑𝑝
𝑑𝑠
= 𝜌𝑣
𝑑𝑣
𝑑𝑠
Se o escoamento e ascendente θ=90°  sen 90° =1
Se for descendente θ=-90°  sen -90° = - 1
Com 𝑣
𝑑𝑣
𝑑𝑠
= 𝑎𝑐𝑒𝑙𝑒𝑟𝑎çã𝑜 = 9,14 𝑚/𝑠2 em escoamento de água
Então para escoamento ascendente:
−9810 ∗ 𝑠𝑒𝑛90 −
𝑑𝑝
𝑑𝑠
= 1000 ∗ 9,14
𝑑𝑝
𝑑𝑠
= −18950,1 𝑁/𝑚3

15. Então para escoamento descendente:
−9810 ∗ 𝑠𝑒𝑛 − 90 −
𝑑𝑝
𝑑𝑠
= 1000 ∗ 9,14
𝑑𝑝
𝑑𝑠
= 670 𝑁/𝑚3

16. 09 – Água escoa na curva bidimensional
mostrada na Figura 1. Note que as linhas de
corrente são circulares e que a velocidade é
uniforme no escoamento. Determine a pressão
nos pontos (2) e (3) sabendo que a pressão no
ponto (1) é igual à 40 kPa.
A equação de pressão total normal à linha de
corrente é dada por:
−𝛾
𝑑𝑧
𝑑𝑛
−
𝜕𝑝
𝜕𝑛
= 𝜌
𝑣2
𝑅
Fazendo o ponto (1) como referencial dn=dz,
portanto
𝑑𝑧
𝑑𝑛
= 1
O raio de curvatura do escoamento será uma
função de n (linha de corrente) assim:
R(n) = 6 – n  quando n=0 o raio será 6 m, ou
seja ponto (1).
A velocidade do escoamento é  v=10m/s
A pressão em (1) é de 40kPa.

17. A equação de pressão total será:
𝑑𝑝
𝑑𝑛
= −𝜌
𝑣2
𝑅(𝑛)
− 𝛾
𝑑𝑝 = −𝜌
𝑣2
𝑅 𝑛
𝑑𝑛 − 𝛾𝑑𝑛
Integrando a equação diferencial de p1 a p2 e n1=0 a n2=n ; com
𝛾, 𝜌 𝑒 𝑣 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡𝑒𝑠 TEM-SE:
𝑑𝑝
𝑝2
𝑝1
= −𝜌𝑣2
𝑑𝑛
6 − 𝑛
𝑛2
0
− 𝛾 𝑑𝑛
𝑛2
0
A solução será:
𝑝2 − 𝑝1 = − 𝜌𝑣2 ln
6
6 − 𝑛
− 𝛾𝑛
𝑑𝑥
(𝑎𝑥 + 𝑏)
=
1
𝑎
(𝑎𝑥 + 𝑏)

18. Para n=1m
𝑝2 − 40000 = − 1000 ∗ 102 ln
6
6 − 1
− 9810 ∗ 1
𝑝2 = 11,9kPa
Para n=2m
𝑝3 − 40000 = − 1000 ∗ 102
ln
6
6 − 2
− 9810 ∗ 2
𝑝3 = −20,2kPa
A pressão sai de ~40kPa para ~-20KPa de uma extremidade para outra
no tubo a redução de pressão é necessária para que o fluido possa
fazer a trajetória.

19. 11 – O manômetro de pressão diferencial conectado a um tubo de pitot foi
modificado para fornecer a velocidade do escoamento diretamente (em lugar da
diferença entre a pressão de estagnação e a estática). A calibração do conjunto foi
realizada com ar na condição atmosférica padrão. Entretanto, o conjunto foi
utilizado para medir a velocidade num escoamento de água e, nesta condição,
indicou que a velocidade era igual a 102,9 m/s. Determine a velocidade real do
escoamento de água.
A função do tubo de pitot é medir a velocidade a partir da diferença de pressão
de acordo com a equação:
𝑣 =
2.∆𝑝
𝜌
 ∆𝑝 =
1
2
𝜌𝑣2
A diferença de entre a velocidade do ar e da água é devido à massa específica
do fluido usado para calibrar, usando a diferença de pressão para a
velocidade de 102,9 como sendo a do ar e igualando ela à diferença de
pressão do escoamento da água pode-se corrigir a velocidade .

20. ∆𝑝𝑎𝑟 = ∆𝑝á𝑔𝑢𝑎
1
2
1,22 ∗ 102,92
=
1
2
1000 ∗ 𝑣2
V=3,6m/s  velocidade da água correta

21. 13 - A Figura seguinte mostra o
esboço de um grande tanque que
contém água e óleo (densidade =
0,7). Admitindo que os efeitos
viscosos são desprezíveis e que o
regime de operação é próximo do
permanente, determine a altura do
jato de água (h) e a pressão do
escoamento no tubo horizontal.
Igualando a pressão total dos pontos
(1) e (4) tem-se:
(1) .
(2) .
(3) .
(4) .
𝑝1 + 𝛾𝑧1 +
1
2
𝜌𝑣1
2
= 𝑝4 + 𝛾𝑧4 +
1
2
𝜌𝑣4
2
Sendo: z1=0 p1=700*9,81*4=27468Pa (pressão da coluna de óleo)
v1=v4=0 p4=0
27468 + 𝛾0 +
1
2
𝜌01
2
= 0 + 𝛾á𝑔𝑢𝑎 𝑧4 +
1
2
𝜌04
2
z4=h=27468/9810=2,8m

22. Resolvido em sala de aula

24. Água escoa em regime permanente na
tubulação mostrada na Figura P3.37. Determine,
para as condições indicadas na figura, o
diâmetro do tubo de descarga (D). Admita que
os efeitos viscosos são desprezíveis.
14

25. Aplicando a equação de Bernoulli nos pontos 1 e 2
teremos:
𝑝1 + 𝛾𝑧1 +
1
2
𝜌𝑣1
2
= 𝑝2 + 𝛾𝑧2 +
1
2
𝜌𝑣2
2
p1= atm=0 (relativa); ϒ=1000.9,81=9810 N/m3;
v1=6,1; z1=3,05m;
p2=ϒh; v2=?; z2=0;
(1)
(2)
14

26. 0 + 9810 𝑥 3,05 + [
1
2
1000𝑥(6,1)2
]
= (4,57 𝑥 9810) + 𝛾0 +
1
2
1000𝑣2
2
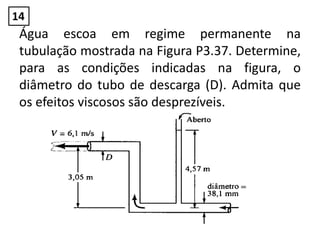
O Problema solicita determinar para as condições
dadas o diâmetro D:
Sabe-se que a vazão é constante, portanto Q1=Q2:
v1A1=V2A2  v2= V1.A1/A2
𝑣2 =
𝑣1.
𝜋𝐷2
4
𝜋(38,1𝑥10−3)2
4
=
6,1𝐷2
(38,1𝑥10−3)2
=
14

27. 0 + 9810 𝑥 3,05 + [
1
2
1000𝑥(6,1)2]
= (4,57 𝑥 9810) + 𝛾0 +
1
2
1000𝑣2
2
9810 𝑥 3,05 + [
1
2
1000𝑥 6,1)2
= (4,57 𝑥 9810) +
1
2
1000
6,1𝐷2
38,1𝑥10−3 2
2
29920,5 + 18605 = 44831,7 + 500 17,659𝑥106
𝐷4
500 17,659𝑥106
𝐷4
= 29920,5 + 18605 − 44831,7
𝐷 =
3693,8
8,829𝑥109
4
= 4,184𝑥10−74
= 𝟎, 𝟎𝟐𝟓𝒎
14

28. Água escoa, em regime permanente, na tubulação
mostrada na Figura P3.71. Admitindo que a água é
incompressível e que os efeitos viscosos são
desprezíveis, determine o valor de h.
(2)
(1)
15

29. (2)
(1)
 Assumindo que o ar é um fluido incompressivel e que a variação de
pressão para pequenas alturas é nula tem-se que a pressão na
interface água/ar será a mesma nas duas interfaces do manômetro
em U;
 O ponto (2) é o bocal contrário ao escoamento, portanto é ponto de
estagnação com velocidade igual a 0 m/s;
 Igualamos a diferença de pressão do manômetro diferencial à
equação de pressão total, ambas rearranjadas em p1-p2 encontra-se
h
15
l

30. Aplicando a equação de Bernoulli aos pontos 1 e 2 teremos:
𝑝1 + 𝛾𝑧1 +
1
2
𝜌𝑣1
2
= 𝑝2 + 𝛾𝑧2 +
1
2
𝜌𝑣2
2
(I)
Sendo: z2= 0 referencial
z1= - 0,91m v1=Q/A1=1,46 m/s
v2=0 ponto de estagnação
Assim a equação (I) fica:
𝑝1 − 𝑝2 = −𝛾𝑧1 −
1
2
𝜌𝑣1
2
(I)
No sistema há um manômetro diferencial entre os ponto 1
e 2, assim a pressão diferencial entre os pontos é dado por:
𝑝2 − 𝛾á𝑔𝑢𝑎 𝑙 − 𝛾á𝑔𝑢𝑎 𝑕 + 𝛾á𝑔𝑢𝑎 𝑙 + 𝛾á𝑔𝑢𝑎0,91 = 𝑝1
−𝛾á𝑔𝑢𝑎 𝑕 + 𝛾á𝑔𝑢𝑎0,91 = 𝑝1 − 𝑝2 (II)
15

31. Igualando (I) e (II):
−𝛾𝑧1 −
1
2
𝜌𝑣1
2
= −𝛾á𝑔𝑢𝑎 𝑕 + 𝛾á𝑔𝑢𝑎0,91
𝑕 =
𝛾á𝑔𝑢𝑎 𝑧1 +
1
2
𝜌𝑣1
2 + (𝛾á𝑔𝑢𝑎(−0,91))
𝛾á𝑔𝑢𝑎
h=0,11m
15

33. 𝑑
𝑑𝑡
𝜌𝑑𝑉 +
𝑣𝑐
𝜌𝑣. 𝑛 𝑑𝐴
𝑠𝑒
= 0
Da equação de conservação de massa temos que:
- Primeiro termo representa a taxa de variação
temporal do volume de controle.
- Segundo termo representa a variação de vazão
em massa do fluido que atravessa a fronteira do
sistema.
17

34. 𝑑
𝑑𝑡
𝜌𝑑𝑉 +
𝑣𝑐
𝜌𝑣. 𝑛 𝑑𝐴
𝑠𝑒
= 0
Integrando o primeiro termo de V = 0 litros até
V= VC l (volume de controle=área da base vezes a
altura h):
𝑑 𝑉
𝑑𝑡
𝜌
O a integração do segundo termo nos dá a
variação de vazão em massa do sistema ( o que sai
menos o que entra:
𝑚2 − 𝑚1
Como não há saída de fluidos do sistema, a vazão
em massa que saí do sistema é nula, pois todo o
fluido é acumulado no interior da piscina.
Assim a equação acima fica:
𝑑 𝑉
𝑑𝑡
𝜌 − 𝑚1 = 0
Dividindo os termos por massa específica termos:

35. 𝑑 𝑉
𝑑𝑡
− 𝑄2 = 0
A vazão de entrada (Q2) é igual à variação temporal de volume
do volume de controle de o até a altura h. Rearranjando a
equação na forma diferencial, tem-se:
𝑑𝑉 = 𝑄𝑑𝑡
Integrando o primeiro termo de h=0 até a altura h=1,5, e o
segundo termo de t=0 até t=t correspondente a altura h, com
a vazão constante de 1l/s (1x10-3m3/s):
Sendo que V é uma função de h: V=Ab.h
𝑑(𝐴 𝑏 𝑕)
𝑕=1,5
0
= 𝑄𝑑𝑡
𝑡
0
𝐴 𝑏. 1,5 = 𝑄. 𝑡
𝐭 =
𝛑𝟓 𝟐
𝟒
. 𝟏, 𝟓
𝟏𝐱𝟏𝟎−𝟑
= 𝟐𝟗𝟒𝟎𝟎𝐬 = ~𝟖 𝐡𝐨𝐫𝐚𝐬

36. Neste problema a vazão de saída não é a mesma de
entrada. Como Qs<Qe haverá acúmulo de água na
represa. O que o problema pede é para determinar
a altura da coluna de água após 24horas ou
86400segundos.
Área= 583 km2=583x106m2
18

37. Da equação de continuidade sabemos que a solução do
primeiro termo nos dá a variação temporal do volume de
controle e que o segundo termo dos dá variação da vazão em
massa:
𝑑
𝑑𝑡
𝜌𝑑𝑉 +
𝑣𝑐
𝜌𝑣. 𝑛 𝑑𝐴
𝑠𝑒
= 0
𝑑
𝑑𝑡
𝜌𝑉𝑣𝑐 + 𝑚 𝑠 − 𝑚 𝑒 = 0
Com Vvc sendo o volume de controle (igual a Asuperfixh) e 𝑚 = 𝑄𝜌
Podemos dividir a equação por massa específica e torna-la em
uma equação diferencial:
𝑑𝑉𝑣𝑐 = (𝑄 𝑒−𝑄𝑠)𝑑𝑡
𝑑(𝐴 𝑠𝑢𝑝. 𝑕) = (𝑄 𝑒−𝑄𝑠)𝑑𝑡
𝑑𝑕 =
(𝑄 𝑒−𝑄𝑠)
𝐴 𝑠𝑢𝑝
𝑑𝑡
Integrando o primeiro termo de h=0 até h=h e de t=0 até t=86400
18

38. 𝑑𝑕
𝑕
0
=
(𝑄 𝑒−𝑄𝑠)
𝐴 𝑠𝑢𝑝
𝑑𝑡
86400
0
𝑕 =
(𝑄 𝑒−𝑄𝑠)
𝐴 𝑠𝑢𝑝
86400
A equação acima nos fornece a altura h que será
preenchida na represa considerando a área,
vazão de entrada e de saída e o temo dado no
problema.
𝑕 =
(1274 − 227)
583x106
86400
h=~0,16m
18

40. Água é retirada do tanque mostrado na
Figura P3.64 por um sifão. Determine a
vazão em volume no escoamento e as
pressões nos pontos (1), (2) e (3). Admita
que os efeitos viscosos são desprezíveis.
(0)
(4)
24

41. Assumindo que o z=0 corresponde ao ponto 0 na
superfície livre e fazendo o eixo positivo apontando
verticalmente para baixo, a pressão no ponto 1 é a
pressão devido a coluna de fluido acima do ponto 1,
portanto:
p1=ρgh
p1=𝛾. 𝑧0 − 𝑧1 = 9810 2,44 = 23936,4Pa=23,9kPa
No ponto 4, descarga do sifão, a água sai devido ao peso
da coluna de fluido, ou seja em jato livre, assim:
𝑣4 = 2𝑔𝑕2
= 2𝑔 𝑧4 − 𝑧0
2
𝑣4 = 2𝑥9,81𝑥 0,91 − 0
2
=4,22m/s
24

42. Como o diâmetro do sifão é de 51 mm nos pontos de
descarga, ponto 3 e ponto 2 (entrada), podemos
concluir que para vazão ser constante (conservação de
massa) as velocidade v4=v3=v2.
Lembre que v=Q/A, sendo A4=A3=A2, então v4=v3=v2
Aplicando a equação de Bernoulli aos pontos 2, 3 e 4,
teremos:
𝑝2 + 𝛾𝑧2 +
1
2
𝜌𝑣2
2
= 𝑝3 + 𝛾𝑧3 +
1
2
𝜌𝑣3
2
= 𝑝4 + 𝛾𝑧4 +
1
2
𝜌𝑣4
2
Levando em conta que:
Z2=2,41m; p2=?; v2=4,22m/s; 𝛾 = 9810𝑁/𝑚3
Z3=0m; p3=?; v3=v2=4,22m/s;
Z4=0,91m; p4=0; v4=v2=4,22m/s;
24

43. Igualando o primeiro termo ao último termo da
igualdade acima, teremos:
𝑝2 + 𝛾𝑧2 +
1
2
𝜌𝑣2
2
= 𝑝4 + 𝛾𝑧4 +
1
2
𝜌𝑣4
2
Como v4=v2=4,22m/s e p4=0, temos:
𝑝2 + 𝛾𝑧2 = 𝛾𝑧4
𝑝2 = 𝛾𝑧4 − 𝛾𝑧2
𝑝2 = 𝛾 𝑧4 − 𝑧2
Sendo: 𝛾 = 9810𝑁/𝑚3; z4=0,91m e Z2=2,44m:
𝑝2 = 9810 0,91 − 2,44 = −𝟏𝟓, 𝟎𝟏𝒌𝑷𝒂
A pressão negativa é responsável por sugar a agua e
fazê-la sair na descarga.
24

44. Igualando o segundo termo ao último termo da
igualdade acima, teremos:
𝑝3 + 𝛾𝑧3 +
1
2
𝜌𝑣3
2
= 𝑝4 + 𝛾𝑧4 +
1
2
𝜌𝑣4
2
Como v3=v2=4,22m/s e p4=0, temos:
𝑝3 + 𝛾𝑧3 = 𝛾𝑧4
𝑝3 = 𝛾𝑧4 − 𝛾𝑧3
𝑝3 = 𝛾 𝑧4 − 𝑧3
Sendo: 𝛾 = 9810𝑁/𝑚3; z4=0,91m e Z3=0m:
𝑝3 = 9810 0,91 − 0 = 𝟖, 𝟗𝟑𝒌𝑷𝒂
𝑄 = 𝑣. 𝐴 = 4,22 ∗
𝜋 0,0512
4
= 8,6𝑥10−3
m3/s
24

45. Extra

46. Da equação de continuidade sabemos que a solução do primeiro
termo nos dá a variação temporal do volume de controle e que o
segundo termo dos dá variação da vazão em massa:
𝑑
𝑑𝑡
𝜌𝑑𝑉 +
𝑣𝑐
𝜌𝑣. 𝑛 𝑑𝐴
𝑠𝑒
= 0
𝑑
𝑑𝑡
𝜌𝑉𝑣𝑐 + 𝑚 𝑠 − 𝑚 𝑒 = 0
Com Vvc sendo o volume de controle (igual a Asuperfixh), 𝑚 = 𝑄𝜌 e
vazão de entrada igual a zero pois só há saída de fluidos, podemos
dividir a equação por massa específica e torná-la em uma equação
diferencial:
𝑑𝑉𝑣𝑐 = (−𝑄𝑠)𝑑𝑡
𝑑(𝐴 𝑠𝑢𝑝. 𝑕) = (−𝑄𝑠)𝑑𝑡
𝑑𝑕 =
(−𝑄𝑠)
𝐴 𝑠𝑢𝑝
𝑑𝑡
Integrando o primeiro termo de h=h1 até h=h2 e de t=t1 até t=t2

47. 𝑑𝑕
𝑕2
𝑕1
=
(−𝑄𝑠)
𝐴 𝑠𝑢𝑝
𝑑𝑡
𝑡2
𝑡1
𝑕1 − 𝑕2 =
−𝑄𝑠
𝐴 𝑠𝑢𝑝
𝑡1 − 𝑡2
A equação acima nos fornece a altura h para
qualquer intervalo de tempo do gráfico dado no
problema.

48. 1) 3 − 𝑕2 =
−1
14,99
0 − 15
−𝑕2= 1 − 3
𝑕2 = 2𝑚
2) 2 − 𝑕2 =
−0
14,99
15 − 25
𝑕2 = 2𝑚
Q(m3/s) Area (m2) d (saída) h1 h2 t1 (s) t2(s)
1 1 14,99 0,564m 3 2 0 15
2 0 14,99 0,564m 2 2 15 25
3 0,2 14,99 0,564m 2 25 115
4 1 14,99 0,564m 115 130
π(4,37)2/4 0,564m

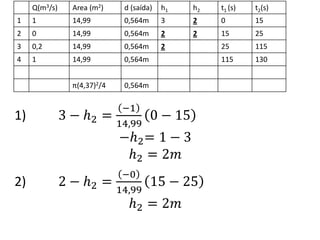
49. 3) 2 − 𝑕2 =
−0,2
14,99
25 − 115
−𝑕2= [−0,01334𝑥 −90 ] − 2
−𝑕2= 1,20 − 2
𝑕2 = 0,8𝑚
4) 0,8 − 𝑕2 =
−1
14,99
115 − 130
−𝑕2= 1,00 − 0,8
−𝑕2= 0,20
𝑕2 = −0,2𝑚
o valor de - 0,2 equivale à altura da tubulação de saída, uma vez que a
altura do reservatório é de 3m.
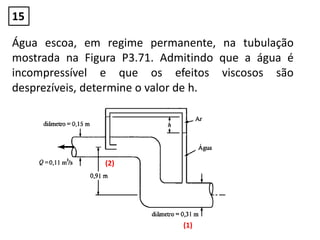
Q(m3/s) Area (m2) d (saída) h1 h2 t1 (s) t2(s)
1 1 14,99 0,564m 3 2 0 15
2 0 14,99 0,564m 2 2 15 25
3 0,2 14,99 0,564m 2 0,8 25 115
4 1 14,99 0,564m 0,8 -0,2 115 130
π(4,37)2/4 0,564m

50. O Problema pede um gráfico da variação de
altura com o tempo para a vazão e as
dimensões do reservatório. Como a vazão é
constante em cada intervalo de tempo
especificado a variação de altura será linear
assim o gráfico terá a seguinte forma:
t(s) h(m)
0 3
15 2
25 2
115 0,8
130 -0,2
0 10 20 30 40 50 60 70 80 90 100 110 120 130 140
-0.4
-0.2
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
2.2
2.4
2.6
2.8
3.0
3.2
3.4
Altura(m)
Tempo (s)

51. Exemplo 3:
Aplicações da Equação de Bernoulli
51

52. A vazão total QT é igual à soma da vazão por
cada orifícios simultaneamente.
Lembre-se que o escoamento se comporta como
jato livre, então:
𝑄 𝑇 = 𝑞1 + 𝑞2 + 𝑞3
𝑄 𝑇 =
𝑉
𝑑𝑡
= −𝐴 𝑇
𝑑𝑕
𝑑𝑡
𝑞1 = 𝐴 𝑜 2𝑔𝑕 = 𝐴 𝑜 2𝑔 𝑕
𝑞2 = 𝐴 𝑜 2𝑔(𝑕 + 𝑙2) = 𝐴 𝑜 2𝑔 (𝑕 + 𝑙2)
𝑞3 = 𝐴 𝑜 2𝑔(𝑕 + 𝑙3) = 𝐴 𝑜 2𝑔 (𝑕 + 𝑙3)
52

53. 𝑄 𝑇 = 𝑞1 + 𝑞2 + 𝑞3
−𝐴 𝑇
𝑑𝑕
𝑑𝑡
= 𝐴 𝑜 2𝑔 𝑕 + 𝐴 𝑜 2𝑔 (𝑕 + 𝑙2) + 𝐴 𝑜 2𝑔 (𝑕 + 𝑙3)
Rearranjando a Equação temos:
𝑑𝑡 = −
𝐴 𝑇
𝐴 𝑜 2𝑔
1
𝑕 + (𝑕 + 𝑙2) + (𝑕 + 𝑙3)
𝑑𝑕
Integrando a Equação de t1=0 a t2=t e h1=h até h2=0
𝑑𝑡
𝑡
0
= −
𝐴 𝑇
𝐴 𝑜 2𝑔
1
𝑕 + (𝑕 + 𝑙2) + (𝑕 + 𝑙3)
𝑑𝑕
0
𝑕
53

54. A solução da integral pode ser mais fácil usando o método de
integração numérica: regra do trapézio;
𝑑𝑡
𝑡
0
= −
𝐴 𝑇
𝐴 𝑜 2𝑔
𝑓 𝑕 𝑑𝑕
0
𝑕
Sendo:
𝑓 𝑕 =
1
𝑕 + (𝑕 + 𝑙2) + (𝑕 + 𝑙3)
Faz-se:
𝑓 𝑕 = 𝑓 𝑕1 + 𝑓 𝑕𝑖 ∗ (𝑕𝑖 − 𝑕1 /2
Indo de h1=0,051 até hi=0 soma-se a n f(h) como solução da
integração.
54

55. 55