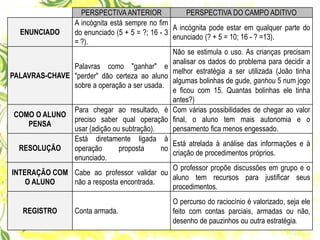
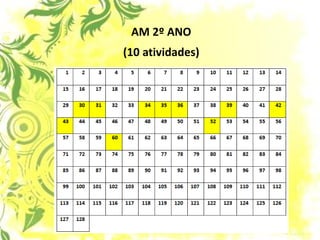
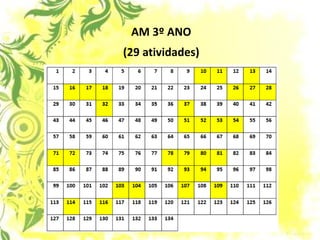
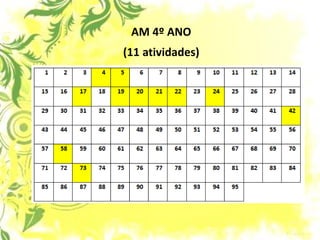
1) O documento discute a subtração e como ensiná-la de forma efetiva para as crianças, propondo abordagens alternativas ao ensino tradicional.
2) É sugerida uma capacitação de professores com discussões e atividades práticas para diagnosticar os conhecimentos dos alunos e planejar novas aulas sobre subtração.
3) O foco é ensinar subtração de forma gradual, explorando as ideias de tirar, comparar e completar através de problemas contextualizados.