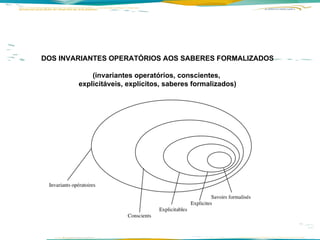
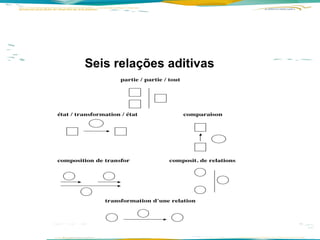
1) O documento discute os campos conceituais como fundamentos da educação e como conceitos e esquemas se desenvolvem ao longo da vida e da interação com situações e outras pessoas. 2) É definida competência como a capacidade de realizar tarefas de maneira adequada e ter recursos alternativos para se adaptar a diferentes circunstâncias. 3) Conceitos, teoremas e regras são discutidos como organizadores dos campos conceituais de estruturas aditivas e multiplicativas.

2. OS CAMPOS CONCEITUAIS COMO FUNDAMENTOS DA EDUCAÇÃO Atividade, metas, conceitos e razão Gérard Vergnaud

3. O QUE É QUE SE DESENVOLVE? Ao mesmo tempo, numa variedade de registros Gestos Competências científicas e técnicas Formas de interação com o outro Atividades de linguagem Afetividade

4. AO LONGO DA VIDA No curto período de tempo de uma conscientização No longo período de tempo da experiência. NA INTERAÇÃO Com as situações Com o outro

5. DEFINIÇÕES DA COMPETÊNCIA 1 « A » é mais competente do que « B » se souber fazer algo que « B » não sabe fazer « A » é mais competente durante um período de tempo t' do que durante um tempo t se ele souber fazer algo que, antes, não sabia fazer. 2 « A » é mais competente se atuar da melhor maneira

6. 3 « A » é mais competente se tiver ao seu dispor um arsenal de recursos alternativos que permitam que ele adapte a sua conduta em função das diferentes circunstâncias que possam ocorrer 4 « A » é mais competente se estiver menos desmunido diante de uma situação

7. OS ESQUEMAS DA ENUMERAÇÃO Esquema elementar - correspondência biunívoca - cardinal . No estádio de Nantes - partilha Card (A U B) = Card(A) + Card(B) - escrita Escrita (soma) = escrita(a) +++ escrita(b) algoritmo da adição - Bloco retangular Card (F X C) = Card(F) * Card(C) X produto cartesiano * multiplicação aritmética Canto do estádio Média= (Nmax + Nmin)/2

8. CONCEITO, TEOREMA, REGRA Conceito-em-ato = conceito considerado pertinente na ação que está sendo executada Teorema-em-ato = proposta considerada como verdadeira Exemplos de regra: não contar duas vezes o mesmo objeto; contá-los todos

9. A MESMA OPERAÇÃO NUMÉRICA TRÊS PROBLEMAS COM DIFERENTES NÍVEIS Pedro tinha 7 bolinhas de gude. Ele ganhou 5. Quantas ele tem agora? Roberto acabou de perder 5 bolinhas de gude; agora ele tem 7. Quantas bolinhas ele tinha antes de jogar?

10. Tiago acabou de jogar 2 partidas de gude. Ele não se lembra mais do que aconteceu na primeira partida. Na segunda partida, ele perdeu 7 bolinhas de gude. Fazendo as contas, ele percebeu que, no total, ele ficou com 5 bolinhas. O que é que aconteceu na primeira partida?

11. Mudanças de sentido Tiago acabou de jogar 2 partidas de gude. Ele não se lembra mais do que aconteceu na primeira partida. Na segunda partida ele bolinhas. Fazendo as contas, ele percebeu que, no total, ele bolinhas. O que é que aconteceu na primeira partida?

12. Mudanças de sentido Tiago acabou de jogar 2 partidas de gude. Ele não se lembra mais do que aconteceu na primeira partida. Na segunda partida ele ganhou 7 bolinhas. Fazendo as contas, ele percebeu que, no total, ele ganhou 15 bolinhas. O que é que aconteceu na primeira partida?

13. Mudanças de sentido Tiago acabou de jogar 2 partidas de gude. Ele não se lembra mais do que aconteceu na primeira partida. Na segunda partida ele ganhou 15 bolinhas. Fazendo as contas, ele percebeu que, no total, ele ganhou 7 bolinhas. O que é que aconteceu na primeira partida?

14. Tiago acabou de jogar 2 partidas de gude. Ele não se lembra mais do que aconteceu na primeira partida. Na segunda partida ele ganhou 15 bolinhas. Fazendo as contas, ele percebeu que, no total, ele ganhou 7 bolinhas. O que é que aconteceu na primeira partida? Mudanças de sentido

15. Seis relações aditivas

16. VÁRIOS ESQUEMAS PARA UMA MESMA SITUAÇÃO André jogou duas partidas de gude e ele tenta saber quantas bolinhas tinha antes de jogar; ao contá-las, ele constata ter 63 bolinhas de gude. Ele se lembra que ganhou 16 bolinhas na primeira partida e perdeu 8 na segunda. Quantas bolinhas ele tinha antes de começar a jogar?

17. Esquema 1: partir da situação final, acrescentar o que ele perdeu e subtrair o que ele ganhou Esquema 2: Formular uma hipótese em relação à situação inicial, aplicando as transformações sucessivas; comparar o resultado obtido com a situação final apresentada no enunciado; corrigir a hipótese em função da diferença entre as duas situações.

18. Esquema 3: compor as duas transformações para saber se, no total, André perdeu ou ganhou bolinhas de gude, e quantas. Aplicar à situação final a transformação recíproca dessa transformação composta.

19. Si F = T(I) então I = T -1 (F) COMO EXPRIMIR OS CONHECIMENTOS UTILIZADOS NA AÇÃO?

20. MULTIPLICIDADE DE SENTIDOS DO SINAL DE « MENOS » Jorge tem 9 euros na sua carteira. Ele quer comprar um doce que custa 3 euros. Quanto lhe sobrará? Ana Lucia tinha 9 euros. Sobraram-lhe 3 euros. Quanto ela gastou?

21. Maria acabou de ganhar 3 euros da sua avó. Agora, ela tem 9 euros. Quanto ela tinha antes de chegar na casa da avó? Teresa convidou 9 crianças para o seu aniversário: meninas e meninos. Havia 3 meninos; quantas meninas havia?

22. A escrita convencional 9 – 3 = não representa a diversidade dos raciocínios que as crianças devem efetuar para decidir que é necessário subtrair 3 de 9

23. Piaget Vygotski esquema Teoria da atividade Invariante operatório Conceito cotidiano / conceito cientifico Função simbólica linguagem e significado das palaras consciência e abstração reflectiva consciência e metacognição interação sujeito / objeto interção adulto / criança Estados e equilibração Zona de desenvolvimento proximal Imitação e interiorização internalização

24. CAMPO CONCEITUAL Conjunto de situações cujo domínio progressivo demanda uma variedade de conceitos, de esquemas e de representações simbólicas em estreita conexão Conjunto de conceitos que contribuem para o domínio dessas situações

25. CONCEITOS ORGANIZADORES DAS ESTRUTURAS ADITIVAS Quantidades discretas e contínuas Medida parte/todo Estado/transformação Comparação referido/referente Composição binária (medidas, transformações, relações)

26. Operação unária Inversão Número natural/número relativo Posição/abscissa/valor algébrico

27. PROPORCIONALIDADE SIMPLES (multiplicação, partição, cotição, quarta proporcional)

28. DOIS CASOS DE PROPORCIONALIDADE 285 kg de cortiça por 0,70 euros o kg Para calcular o custo total, é necessário fazer uma multiplicação ou uma divisão? 0,70 toneladas de concreto por 285 euros a tonelada Para calcular o custo total, é necessário fazer uma multiplicação ou uma divisão?

29. ANÁLISE CONCEITUAL DOS DOIS CASOS A escolha da operação correta poderá ser contestada pelo caráter crescente da função E pela falsa ideia de que a multiplicação fornece um resultado maior do que a divisão

30. 1 o,70 285 custo escalar maior que 1 285  1 f (285)  f (1) não há problema! 1 285 0,7 custo escalar menor que 1 0,7  1 f (0,7)  f (1) Problema!

31. Conceito = ( S, I, L) conjunto de situações que dão sentido ao conceito I conjunto de invariantes operatórios que fundamentam a operacionalidade dos esquemas L conjunto de formas simbólicas e de linguagem que permitem que se tenha uma representação dos conceitos, das situações e das formas de tratamento

32. CONCEITOS E TEOREMAS ORGANIZADORES DAS ESTRUTURAS MULTIPLICATIVAS Multiplicação/divisão; proporcionalidade; grandezas e dimensões; função linear, bilinear, n-linear; escalar, produto e quociente de dimensões

33. Teoremas-em-ato isomorfismos da função linear f(x + x') = f(x) + f(x') f(nx) = nf(x) f(nx + n'x') = nf(x) + n'f(x') f(n) = nf(1) Casos particulares f(1) = f(n)/n n = f(n)/f(1) coeficiente de proporcionalidade f(x) = ax x = 1/a f(x) produto cruzado e regra de três x' * f(x) = x * f(x’) f(x') = x' * f(x) / x dupla linearidade f (n 1 x 1 , n 2 x 2 ) = n 1 n 2 f(x 1 , x 2 )

34. DOS INVARIANTES OPERATÓRIOS AOS SABERES FORMALIZADOS (invariantes operatórios, conscientes, explicitáveis, explícitos, saberes formalizados)

35. Simetria ortogonal

36. Simetria ortogonal Quatro formas predicativas com diferentes níveis 1 - A fortaleza é simétrica 2 - O triângulo A'B'C' é simétrico ao triângulo ABC em relação à reta d 3 - A simetria mantém os comprimentos e os ângulos 4 - A simetria é uma isometria

37. OBRIGADO