Este documento apresenta os principais conceitos sobre probabilidades e combinatória. Discute propriedades de operações com eventos, a lei de Laplace, axiomas de probabilidade, probabilidade condicionada, independência de eventos e teoremas associados. Apresenta também conceitos sobre cálculo combinatório como fatorial, permutações, arranjos e combinações.

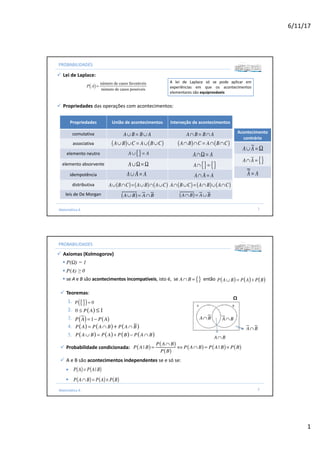
1. 6/11/17
1
PROBABILIDADES
ü Propriedades das operações com acontecimentos:
ü Lei de Laplace:
P A( )=
número de casos favoráveis
número de casos possíveis
Propriedades União de acontecimentos Interseção de acontecimentos
comutativa
associativa
elemento neutro
elemento absorvente
idempotência
distributiva
leis de De Morgan
1Matemática A
A∩ B = B∩ AA∪ B = B∪ A
A∪ B( )∪C = A∪ B∪C( ) A∩ B( )∩C = A∩ B∩C( )
A∪ B∩C( )= A∪ B( )∩ A∪C( )
A ∪{}= A A∩Ω = A
A∪Ω = Ω A∩{}= {}
A∪ A = A A∩ A = A
A∩ B∪C( )= A∩ B( )∪ A∩C( )
A ∪ B( )= A ∩ B A∩ B( )= A∪ B
A lei de Laplace só se pode aplicar em
experiências em que os acontecimentos
elementares são equiprováveis
Acontecimento
contrário
A∪ A = Ω
A∩ A = {}
A = A
PROBABILIDADES
ü Axiomas (Kolmogorov)
§ P(Ω) = 1
§ P(A) ≥ 0
§ se A e B são acontecimentos incompatíveis, isto é, se então
2Matemática A
ü Probabilidade condicionada: P A | B( )=
P A ∩ B( )
P B( )
⇔ P A ∩ B( )= P A | B( )× P B( )
ü A e B são acontecimentos independentes se e só se:
§
§
P A( )= P A | B( )
P A∩ B( )= P A( )× P B( )
ü Teoremas:
1.
2.
3.
4.
5.
P {}( )= 0
P A ∪ B( ) = P A( )+ P B( )− P A ∩ B( )
0 ≤ P A( ) ≤1
P A( )= 1− P A( )
A∩ B
A∩ B A∩ B
A∩ B
Ω
A∩ B = {} P A ∪ B( ) = P A( )+ P B( )
P A( ) = P A ∩ B( )+ P A ∩ B( )

2. 6/11/17
2
PROBABILIDADES
ü Árvore de Probabilidades:
3Matemática A
ü Tabela de contingência:
Total
Total 1 (100%)
P A( )A
A P A( )
P B( )P B( )
B B
P A∩ B( ) P A∩ B( )
P A∩ B( ) P A∩ B( )
P B | A( ) P A ∩ B( )
P A( )
B
P A( )
P B | A( )
P B | A( ) B
B
B
P A ∩ B( )
P A ∩ B( )
P B | A( ) P A ∩ B( )
A
A
P B( )
P B( )
ANÁLISE COMBINATÓRIA
0!= 1
1!= 1
ü Cálculo combinatório
§ fatorial de um número natural n:
§ permutações de n elementos distintos:
§ arranjos sem repetição:
§ arranjos com repetição:
§ combinações:
n!= n × n −1( )× n − 2( )×...× 3× 2 ×1
Pn = n!
n
Ap =
n!
n − p( )!n
A'
p = np
n
Cp =
n
Ap
p!
=
n!
p! n − p( )!
Entram todos os
elementos na
sequência?
Permutações
Sim
Arranjos com
repetição
Não
Sim Não
Arranjos sem repetição
Não
Importa a ordem
dos elementos?
Sim
Os elementos
repetem-se?
Não
Os elementos
repetem-se?
Combinações
ü Síntese
4Matemática A

3. 6/11/17
3
ANÁLISE COMBINATÓRIA
ü Triângulo de Pascal
ü Binómio de Newton:
§ Termo geral do desenvolvimento:
O desenvolvimento de (a+b)n tem n+1 termos
O grau de cada monómio é igual a n
5Matemática A
ü Propriedades do triângulo de Pascal:
§ O primeiro e último elemento de qualquer linha do triângulo é sempre 1:
§ Em cada linha os elementos equidistantes dos extremos são iguais:
§ A soma de dois elementos consecutivos de uma linha, é igual ao elemento que se encontra
entre eles na linha seguinte:
§ A linha de ordem n tem (n+1) elementos
§ A soma de todos os elementos da linha de ordem n é igual a 2n :
§ O segundo e o penúltimo elementos da linha n é igual a n:
n
C0 = n
Cn = 1, n ∈N0
n
Cp = n
Cn− p n, p ∈N0, p ≤ n
n
Cp + n
Cp+1 = n+1
Cp+1 n, p ∈N0, p ≤ n
n
C0 + n
C1 + ...+ Cn = 2n
, n ∈N0
n
C1 = n
Cn−1 = n
Tp+1 = n
Cp × an− p
× bp
a + b( )n
= n
Ck
k=0
n
∑ × an−k
× bk
, n, p ∈N0, p ≤ n
PROBABILIDADES E COMBINATÓRIA
ü Distribuição de probabilidades:
§ Valor médio ou esperado:
§ Desvio padrão:
ü Distribuição binomial: B(n,p)
6Matemática A
ü Distribuição normal: N(µ,σ)
§
§
§
µ = p1 x1 + ...+ pn xn
σ = p1 x1 − µ( )2
+ ...+ pn xn − µ( )2
P X = k( )= n
C´k × pn
× 1− p( )n−k
, 0 ≤ k ≤ n
P µ −σ < X < µ +σ( )≈ 0,6827
P µ − 2σ < X < µ + 2σ( )≈ 0,9545
P µ − 3σ < X < µ + 3σ( )≈ 0,9973
xi x1 x2 … xn
P(X=xi) p1 p2 … pn
pi = 1
i=1
n
∑
Só estamos perante um processo de provas
repetidas se efetuamos a mesma experiência
repetidas vezes, nas mesmas condições

4. 6/11/17
4
FUNÇÕES
7Matemática A
Generalidades
Função injetiva
objetos diferentes têm
sempre imagens diferentes
Função par
O gráfico é simétrico em
relação ao eixo das ordenadas
Função ímpar
O gráfico é simétrico em
relação à origem do referencial
∀x1,x2 ∈Df : x1 ≠ x2 ⇒ f x1( )≠ f x2( )
∀x1,x2 ∈Df : f x1( )= f x2( )⇒ x1 = x2
∀x ∈Df : f −x( )= f x( )
∀x ∈Df : f −x( )= − f x( )
Transformações de gráficos (k > 0)
Os gráficos de f e g são simétricos em relação ao eixo das abcissas
Os gráficos de f e g são simétricos em relação ao eixo das ordenadas
O gráfico de g desloca-se, em relação ao de f, k unidades para cima
O gráfico de g desloca-se, em relação ao de f, k unidades para baixo
O gráfico de g desloca-se, em relação ao de f, k unidades para a esquerda
O gráfico de g desloca-se, em relação ao de f, k unidades para a direita
g x( )= − f x( )
g x( )= f −x( )
g x( )= f x( )+ k
g x( )= f x( )− k
g x( )= f x + k( )
g x( )= f x − k( )
Regras
Definições
FUNÇÕES
8Matemática A
ax
× ay
= ax+y
ax
× bx
= a × b( )x
ax
ay
= ax−y
ax
bx
=
a
b
⎛
⎝⎜
⎞
⎠⎟
x
ax
( )
y
= axy
üPotências:
a−n
=
1
an
an
( )
k
= a
k
n
a1
= a
a0
= 1

5. 6/11/17
5
SUCESSÕES
ü Monotonia de uma sucessão (un)
§ monótona crescente se:
§ monótona decrescente se:
un+1 − un ≥ 0, ∀n ∈N
un+1 − un ≤ 0, ∀n ∈N
ü Progressões
Progressão aritmética Progressão geométrica
Razão
Termo geral
Soma dos n primeiros
termos
r = un+1 − un r =
un+1
un
un = u1 + n −1( )× r
un = uk + k −1( )× r
Sn =
u1 + un
2
× n Sn = u1 ×
1− rn
1− r
9Matemática A
lim 1+
1
n
⎛
⎝⎜
⎞
⎠⎟
n
= e
un = u1 × rn−1
un = uk × rn−k
FUNÇÕES
10Matemática A
Função Domínio Expressão
soma
diferença
produto
quociente
composta
inversa
Df +g = Df ∩ Dg
Df −g = Df ∩ Dg
Df ×g = Df ∩ Dg
Df +g = Df ∩ Dg x ∈R :g x( )= 0{ }
f + g( ) x( )= f x( )+ g x( )
f − g( ) x( )= f x( )− g x( )
f × g( ) x( )= f x( )× g x( )
f
g
⎛
⎝⎜
⎞
⎠⎟ x( )=
f x( )
g x( )
Dgo f = x : x ∈Df ∧ f x( )∈Dg{ } go f( ) x( )= g f x( )⎡⎣ ⎤⎦
Df −1 = D'f f −1
b( )= a ⇔ f a( )= b
Não se deve confundir f -1 com 1
f

6. 6/11/17
6
FUNÇÕES
11Matemática A
(a > 1)
Função exponencial:
f (x) = ax
Função logarítmica:
f (x) = logax
Domínio
Contradomínio
Interseção com o
eixo das ordenadas
no ponto (0, 1)
no ponto (1, 0)
1 é zero da função
Interseção com o
eixo das ordenadas
não tem zeros
não interseta este eixo
Monotonia
estritamente crescente estritamente crescente
Injetiva
sim sim
Limites
ax
= ay
⇔ x = y
ax
< ay
⇔ x < y
a−∞
= 0
a+∞
= +∞
R
R+
ax
> 0
R
R+
loga x < loga y ⇔ x < y
A inversa da função
exponencial de base a é a
função logarítmica de base a
loga x = loga y ⇔ x = y
loga 0+
= −∞
loga +∞( )= +∞
Propriedades operatóriasConsequências da
definição
FUNÇÕES
12Matemática A
ü Logaritmo de um número numa dada base a (a >1):
loga x = y ⇔ ay
= x
loga a = 1
loga 1= 0
loga ax
( )= x
aloga x
= x
loga xy( )= loga x + loga y
loga
x
y
⎛
⎝⎜
⎞
⎠⎟ = loga x − loga y
loga
1
x
= −loga x
loga xk
( )= k loga x
loga xn
=
1
n
loga x
Fórmula de mudança
de base
loga x =
logb x
logb a

7. 6/11/17
7
LIMITES
13Matemática A
Álgebra dos limites
Adição (+ ∞) + (+∞) = + ∞ (− ∞) + (− ∞) = − ∞ a + (+∞) = + ∞ a + (−∞) = − ∞
Multiplicação
(mantém-se a
regra dos sinais)
∞ × ∞ = ∞ a × ∞ = ∞ (a ≠ 0)
Divisão
(mantém-se a
regra dos sinais)
Potenciação
(mantém-se a
regra dos sinais)
∞n = ∞
Radiciação
(mantém-se a
regra dos sinais)
Símbolos de
indeterminação
+ ∞ − ∞ 0 × ∞
0
0
∞
a
= ∞
a
∞
= 0
∞
∞
a ∈R, n ∈N
a
0
= ∞ a ≠ 0( )
+∞n
= +∞ −∞n
= −∞ n ímpar( )
LIMITES
14Matemática A
ü Definição de limite de uma função segundo Heine:
Dizemos que se, e só se, qualquer que seja a sucessão (xn), que tenha todos os seus
elementos pertencentes ao domínio de f e que tenda para a, por valores diferentes de a, a
correspondente sucessão das imagens f (xn) converge para b
lim
x→a
f x( )= b
ü Limites laterais:
Supondo que faz sentido falar nos limites laterais e dizemos que existe
se, e só se os dois limites laterais existirem e forem iguais, sendo:
lim
x→a−
f x( ) lim
x→a+
f x( )
lim
x→a
f x( )
lim
x→a
f x( )= lim
x→a−
f x( )= lim
x→a+
f x( )

8. 6/11/17
8
LIMITES
15Matemática A
Indeterminação Tipo de função Como levantar a indeterminação
∞ − ∞
Polinomial
Colocar em evidência o termo de maior grau ou selecionar o termo
de maior grau do polinómio
Irracional Multiplicar e dividir a expressão pelo seu conjugado
Racional
Colocar em evidência o termo de maior grau no numerador e no
denominador ou selecionar o termo de maior grau no numerador e
no denominador
Irracional
Depende do tipo de expressão: simplificar a expressão ou multiplicar
e dividir pelo radical
Racional
Fatorizar o numerador e o denominador de modo a simplificar a
expressão
Irracional Multiplicar e dividir a expressão pelo seu conjugado
0 × ∞ - Efetuar o produto, obtendo-se uma das indeterminações anteriores
0
0
∞
∞
Nas funções exponenciais e logarítmicas levanta-se as indeterminações recorrendo aos limites
notáveis:
lim
x→+∞
ln x
x
= 0 lim
x→0
ln x +1( )
x
= 1lim
x→0
ex
−1
x
= 1lim
x→+∞
ex
xp
= +∞
CONTINUIDADE
16Matemática A
ü Função contínua no ponto a (não isolado) do seu domínio:
§ Se dizemos que a função f é contínua no ponto a
§ Se não existir ou se dizemos que a função f não é contínua no
ponto a
lim
x→a
f x( )= f a( )
lim
x→a
f x( ) lim
x→a
f x( )≠ f a( )
Uma função f é contínua à direita, num ponto a do seu domínio se
Uma função f é contínua à esquerda, num ponto a do seu domínio se
Se uma função é contínua à direita e é contínua à esquerda, num ponto, então é contínua nesse
ponto
lim
x→a+
f x( )= f a( )
lim
x→a−
f x( )= f a( )
Uma função f é contínua no intervalo aberto ]a, b[ contido no seu domínio, se for contínua em todos
os pontos do intervalo
Uma função f é contínua no intervalo fechado [a, b] contido no seu domínio, se for contínua no
intervalo aberto ]a, b[ , contínua à direita no ponto a e contínua à esquerda no ponto b
Uma função f é contínua se for contínua em todos os pontos do domínio

9. 6/11/17
9
TEOREMA DE BOLZANO
17Matemática A
ü Teorema de Bolzano:
Seja f uma função contínua no intervalo [a, b]
Seja k um número real entre f (a) e f (b) : f (a) < k < f (b)
Então existe pelo menos um número real c entre a e b cuja imagem é k : ∃c ∈ a,b] [: f c( )= k
ü Corolário do teorema de Bolzano:
Seja f uma função contínua no intervalo [a, b]
Se f (a) e f (b) tiverem sinais contrários: f (a) × f (b) < 0
Então a função tem pelo menos um zero entre a e b : ∃c ∈ a,b] [: f c( )= 0
ASSÍNTOTAS
18Matemática A
ü Assíntota horizontal:
A reta de equação y =b é uma assíntota horizontal do gráfico da função f , quando se,
e só se (sendo b um número real)
x → ±∞
lim
x→±∞
f x( ) = b
ü Assíntota vertical
A reta de equação x =a é uma assíntota vertical do gráfico da função f se, e só:
e/ou
lim
x→a−
f x( )= ±∞
lim
x→a+
f x( )= ±∞
ü Assíntota não vertical:
A reta de equação y = m x +b é assíntota não vertical do gráfico da função f , quando
se, e só se:
lim
x→±∞
f x( )− mx + b( )⎡⎣ ⎤⎦ = 0 lim
x→±∞
f x( )− mx⎡⎣ ⎤⎦ = b lim
x→±∞
f x( )
x
= m
x → ±∞
O gráfico de uma função não tem qualquer assíntota
vertical se a função for contínua e tiver por domínio o
conjunto ou um intervalo fechadoR
Se m = 0 a reta é uma assíntota horizontal
Se não existe assíntota oblíquam ∉R

10. 6/11/17
10
DERIVADAS
19Matemática A
ü Taxa média de variação :
Seja f uma função e seja [a, b] um intervalo contido no domínio de f
Chama-se taxa média de variação de f no intervalo [a, b], com a ≠ b ao valor tmv a,b[ ] =
f b( )− f a( )
b − a
ü Derivada de uma função num ponto:
Seja f uma função e seja a um ponto contido do seu domínio
Chama-se derivada da função f no ponto a ao limite (se existir)
ou
f '
a( )= lim
x→a
f x( )− f a( )
x − a
f '
a( )= lim
h→0
f a + h( )− f a( )
h
A derivada de uma função num ponto representa geometricamente o
declive da reta tangente ao gráfico da função nesse ponto
Toda a função com derivada finita num ponto é contínua nesse ponto
DERIVADAS
20Matemática A
- Quando as derivadas laterais num ponto são iguais, existe derivada da função nesse ponto
- Quando as derivadas laterais num ponto são diferentes, não existe derivada da função
nesse ponto
ü Derivadas laterais:
Seja f uma função e seja a um ponto contido do seu domínio
§ Chama-se derivada lateral esquerda da função f no ponto a ao limite (se existir)
ou
§ Chama-se derivada lateral direita da função f no ponto a ao limite (se existir)
ou
f '
a−
( )= lim
x→a−
f x( )− f a( )
x − a
f '
a−
( )= lim
h→0−
f a + h( )− f a( )
h
f '
a+
( )= lim
x→a+
f x( )− f a( )
x − a
f '
a+
( )= lim
h→0+
f a + h( )− f a( )
h
Pode não fazer sentido determinar pelo menos uma das derivadas
laterais de uma função num ponto do seu domínio

11. 6/11/17
11
DERIVADAS
21Matemática A
Derivada Regras de derivação
constante (k)’ = 0
soma (u + v)’ = u’+ v’
produto (k u)’ = k u’ (u × v)’ = u’ v + u v’
quociente
potência (un)’ = n un-1 u’
raiz quadrada
função exponencial de base e (ex)’ = ex (eu)’ = eu u’
função exponencial de base a (ax)’ = ax ln a (au)’ = u’au ln a
função logarítmica de base e
função logarítmica de base a
função composta (g o f)’ (x) = f’(x) × g’ [ f(x)]
1
v
⎛
⎝⎜
⎞
⎠⎟
'
= −
v'
v2
u
v
⎛
⎝⎜
⎞
⎠⎟
'
=
u'v − uv'
v2
x( )
'
=
1
2 x
u( )
'
=
u'
2 u
ln x( )'
=
1
x
lnu( )'
=
u'
u
loga x( )'
=
1
xlna
loga u( )'
=
u'
ulna
DERIVADAS
22Matemática A
ü Monotonia e extremos:
Método para o estudo de uma função, quanto à monotonia e aos extremos:
1. determinar a derivada da função
2. determinar os zeros da derivada
3. elaborar um quadro, no qual se estabelece a relação entre o sinal e os zeros da derivada com
a monotonia e os extremos da função
Um zero da derivada só corresponde a um
extremo da função, se a derivada mudar de
sinal desse ponto (1)
- se a derivada passar de negativa a
positiva, a função tem um mínimo
- se a derivada passar de positiva a
negativa, a função tem um máximo
- Se f’(x) ≥ 0 para qualquer então a
função f é crescente em I
- Se f’(x) ≤ 0 para qualquer então a
função f é decrescente em I
x ∈I
x ∈I
Sabendo que f’(x) = 0:
- se f’’(a) < 0 então a função f tem um máximo para x = a
- se f’’(a) > 0 então a função f tem um mínimo para x = a
(1) Se a função não for
contínua nesse ponto, esta
análise é realizada após o
cálculo das derivadas laterais
Ter em atenção o domínio da função e da 1.ª derivada

12. 6/11/17
12
DERIVADAS
23Matemática A
ü Concavidade e pontos de inflexão:
Método para o estudo de uma função, quanto ao sentido das concavidades e existência de pontos
de inflexão:
1. determinar a segunda derivada da função
2. determinar os zeros da segunda derivada
3. elaborar um quadro, no qual se estabelece a relação entre o sinal e os zeros da segunda
derivada com o sentido das concavidades e pontos de inflexão do gráfico da função
O ponto (a, f(a)) é um ponto de
inflexão do gráfico da função f , se
nesse ponto, o gráfico de f mudar o
sentido da concavidade
- O gráfico da função f tem a concavidade voltada
para cima em I se, e só se
- O gráfico da função f tem a concavidade voltada
para baixo em I se, e só se
f '' x( )> 0, ∀x ∈I
f '' x( )< 0, ∀x ∈I
Ter em atenção o domínio da função e da 2.ª derivada
TRIGONOMETRIA
24Matemática A
ü Razões trigonométricas num triângulo retângulo:
senα =
cateto oposto
hipotenusa
=
a
c
cosα =
cateto adjacente
hipotenusa
=
b
c
tgα =
cateto oposto
cateto adjacente
=
a
b
ü Valores e sinal de algumas razões trigonométricas:
α
(30°) (45°) (60°)
sen α
cos α
tg α 1
π
2
π
3π
2
2ππ
6
π
4
π
3
1
2
1
2
3
2
3
2
2
2
2
2
3
3
3
α 0 1.º Q 2.º Q 3.º Q 4.º Q
sen α 0 + 1 + 0 − -1
−
0
cos α 1 + 0 − -1 − 0 + 1
tg α 0 +
n
d
− 0 +
n
d
−
0
π
2
π
3π
2
2π
Equações trigonométricas
senx = senα ⇔ x =α + 2kπ ∨ x = π −α + 2kπ, k ∈Z
cosx = cosα ⇔ x =α + 2kπ ∨ x = −α + 2kπ, k ∈Z
tgx = tgα ⇔ x =α + kπ, k ∈Z

13. 6/11/17
13
TRIGONOMETRIA
25Matemática A
ü Redução ao 1.º quadrante:
π
2
π
3π
2
2π
----- ----- ----- -----
π −α−α π +α
π
2
−α
π
2
+α
3π
2
−α
3π
2
+α
sen −α( )= −senα
cos −α( )= cosα
tg −α( )= −tgα
sen π −α( )= senα
cos π −α( )= −cosα
tg π −α( )= −tgα
sen π +α( )= −senα
cos π +α( )= −cosα
tg π +α( )= tgα
sen
π
2
−α
⎛
⎝⎜
⎞
⎠⎟ = cosα
cos
π
2
−α
⎛
⎝⎜
⎞
⎠⎟ = senα
sen
π
2
+α
⎛
⎝⎜
⎞
⎠⎟ = cosα
cos
π
2
+α
⎛
⎝⎜
⎞
⎠⎟ = −senα
sen
3π
2
−α
⎛
⎝⎜
⎞
⎠⎟ = −cosα
cos
3π
2
−α
⎛
⎝⎜
⎞
⎠⎟ = −senα
sen
3π
2
+α
⎛
⎝⎜
⎞
⎠⎟ = −cosα
cos
3π
2
+α
⎛
⎝⎜
⎞
⎠⎟ = senα
ü Fórmulas trigonométricas:
Fórmulas básicas Fórmulas da soma e da diferença Fórmulas do ângulo duplo
sen2
α + cos2
α = 1
tgα =
senα
cosα
1+ tg2
α =
1
cos2
α
sen 2α( )= 2senα cosα
sen α + β( )= senα cosβ + cosα senβ
sen α − β( )= senα cosβ − cosα senβ
cos α + β( )= cosα cosβ − senα senβ
cos α − β( )= cosα cosβ + senα senβ
tg α + β( ) =
tgα + tgβ
1− tgα tgβ
tg α − β( ) =
tgα − tgβ
1+ tgα tgβ
cos 2α( )= cos2
α − sen2
α
tg 2α( ) =
2tgα
1− tg2
α
TRIGONOMETRIA
26Matemática A
π
2
π
3π
2
2π
Funções: f (x) = sen x f (x) = cos x f (x) = tg x
Domínio
Contradomínio
Período Positivo mínimo: Positivo mínimo: Positivo mínimo:
Maximizantes Não tem extremos
(é crescente em qualquer
intervalo onde está definida)Minimizantes
Zeros
Continuidade Contínua em Contínua em Contínua no seu domínio
Simetrias Impar: Par: Impar:
Gráfico
Existe uma infinidade de
assíntotas verticais
−1,1[ ] −1,1[ ]
tg x = 0 ⇔ x = kπ, k ∈Z
sen x = 1⇔ x =
π
2
+ 2kπ, k ∈Z
R R
sen x = −1⇔ x = −
π
2
+ 2kπ, k ∈Z
sen x = 0 ⇔ x = kπ, k ∈Z
R
sen −x( )= −sen x
cos x = 1⇔ x = 2kπ, k ∈Z
cos x = −1⇔ x = π + 2kπ, k ∈Z
cos x = 0 ⇔ x =
π
2
+ kπ, k ∈Z
R
cos −x( )= cos x
x ∈R : x ≠
π
2
+ kπ, k ∈Z
⎧
⎨
⎩
⎫
⎬
⎭
R
tg −x( )= −tg x
2π 2π π

14. 6/11/17
14
TRIGONOMETRIA
27Matemática A
π
2
π
3π
2
2π
ü Derivadas:
§
§
§
sen x( )' = cos x senu( )' = u'cosu
cos x( )' = −sen x cosu( )' = −u'senu
tg x( )' =
1
cos2
x
tgu( )' =
u'
cos2
u
ü Limites
§ Não existem os seguintes limites:
§
§ Limite notável:
lim
x→±∞
sen x
lim
x→±∞
cos x
lim
x→±∞
tg x
lim
x→0
sen x
x
= 1
lim
$→±'
sin 𝑥
𝑥
= 0
COMPLEXOS
28Matemática A
π
2
π
3π
2
2π
Para dividir dois números
complexos, multiplicamos o
numerador e o denominador pelo
conjugado do denominador
ü Números complexos na forma algébrica
§ Conjunto dos números complexos:
- a é a parte real do número complexo z = a + bi: Re(z) = a
- bi é a parte imaginária do número complexo z = a + bi
- b é o coeficiente da parte imaginária do número complexo z = a + bi: Im(z) = b
§ Simétrico de um número complexo:
§ Conjugado de um número complexo:
§ Igualdade de números complexos:
§ Adição e subtração de números complexos:
§ Multiplicação de números complexos:
§ Divisão de números complexos:
a + bi( )± c + di( )= a ± c( )+ b ± d( )i
a + bi( )× c + di( )= ac − bd( )+ ad + bc( )i
a + bi
c + di
=
a + bi( )× c − di( )
c + di( )× c − di( )
£ = z = a + bi :a,b ∈R e i = −1{ }
a + bi = c + di ⇔ a = c ∧ b = d
z = a + bi = a − bi
−z = − a + bi( )= −a − bi

15. 6/11/17
15
COMPLEXOS
29Matemática A
π
2
π
3π
2
2π
ü Representação geométrica de um número complexo no plano complexo (ou de Argand)
§ imagem geométrica ou afixo do número complexo z = a + bi: ponto P(a,b)
§ Imagem vetorial do número complexo z: vetor OP
u ruu
P (a, b)
eixo real
eixo imaginário
Im(z)
Re(z)O a
bü Propriedades:
§
§
§
§
z( )
z + z = 2Re z( )
z × z = z
2
z + w = z + w z × w = z × w
z − z = 2Im z( )i
z
w
⎛
⎝⎜
⎞
⎠⎟ =
z
w
ü Potências de base i :
in
= i4 p+r
= ir
, r ∈ 0,1,2,3{ } n 4
r p
No plano complexo, a distância
entre os afixos dos números
complexos z e w é igual a |z – w|
COMPLEXOS
30Matemática A
π
2
π
3π
2
2π
ü Números complexos na forma trigonométrica
§ Forma trigonométrica de um número complexo:
- ρ é a módulo do número complexo z = a + bi:
- α é o argumento do número complexo z = a + bi:
. α é o argumento positivo mínimo de z:
. α é o argumento principal de z:
§ Simétrico de um número complexo:
§ Conjugado de um número complexo:
§ Inverso de um número complexo:
§ Igualdade de números complexos:
§ Multiplicação de números complexos:
§ Divisão de números complexos:
§ Potenciação:
§ Radiciação: o número complexo z tem n raízes de índice n dadas por:
z = ρ cisα = ρ cosα + i senα( )
z = ρ = a2
+ b2
arg z( )= α : tgα =
b
a
a ≠ 0( )
α ∈ 0,2π[ [
α ∈ −π,π] ]
−z = − ρ cisα( )= ρ cis π +α( )
z = ρ cisα = ρ cis −α( )
ρ1 cisα1 = ρ2 cisα2 ⇔ ρ1 = ρ2 ∧ α1 −α2 = 2kπ, k ∈Z
ρ1 cisα1( )× ρ2 cisα2( )= ρ1 ρ2 cis α1 +α2( )
ρ1 cisα1
ρ2 cisα2
=
ρ1
ρ2
cis α1 −α2( )
1
ρ cisα
=
1
ρ
cis −α( )
zn
= ρn
cis nα( )
ρ cis
α + 2kπ
n
k ∈ 0,1,...,n −1{ }
A partir do conhecimento de uma das raízes de
índice n de um número complexo, podemos
obter as restantes raízes, adicionado
sucessivamente ao argumento2π
n
As imagens geométricas
das raízes de índice n de
um número complexo são
vértices de um polígono
regular de n lados

16. 6/11/17
16
COMPLEXOS
31Matemática A
π
2
π
3π
2
2π
Condições em
Reta vertical que passa pelo ponto (a,0) Re(z) = a
Semiplano fechado situado à direita da reta x = a Re(z) ≤ a
Reta horizontal que passa pelo ponto (0, b) Im(z) = b
Semiplano aberto superior à reta y = b Im(z) > b
Circunferência de centro no afixo de z1 e raio r |z – z1| = r
Círculo de centro no afixo de z1 e raio r |z – z1| ≤ r
Exterior ao círculo de centro no afixo de z1 e raio r |z – z1| > r
Coroa circular de centro no afixo de z1 e raios r1 e r2 r1 ≤ |z – z1| ≤ r2
Mediatriz do segmento de reta cujos extremos são os afixos de z1 e z2 |z – z1| = |z – z2|
Semiplano fechado que contém o afixo de z1 |z – z1| ≤ |z – z2|
Semiplano aberto que contém o afixo de z2 |z – z1| > |z – z2|
Semirreta com origem em O que forma um ângulo de amplitude θ com o semieixo real
positivo
arg(z) = θ
Semirreta de origem no afixo de z1 que forma um ângulo de amplitude θ com a semirreta de
origem no afixo de z1 e com a direção e sentido do semieixo real positivo
arg(z-z1) = θ
Ângulo de vértice no afixo de z1 em que os lados fazem ângulos de amplitudes θ1 e θ2 com a
semirreta de origem no afixo de z1 e com a direção e sentido do semieixo real positivo θ1 < arg(z-z1) < θ2
£