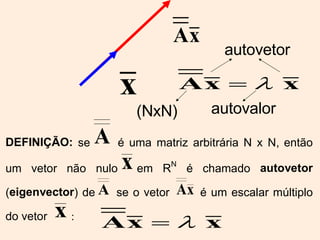
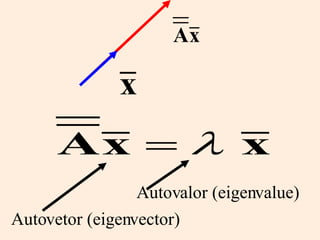
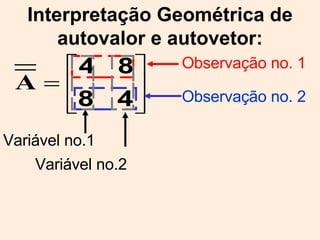
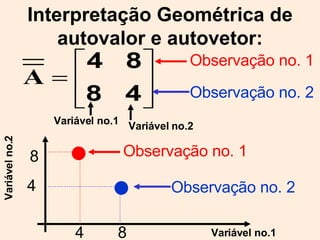
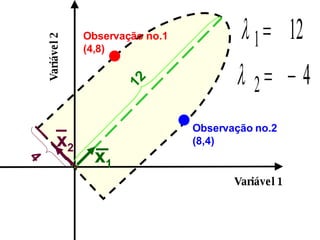
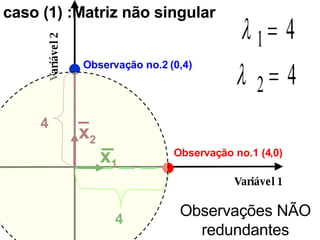
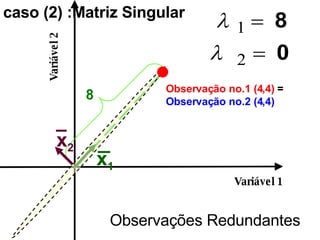
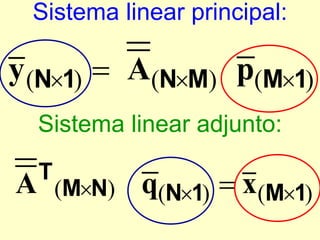
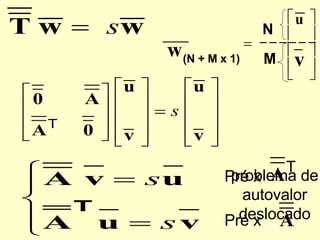
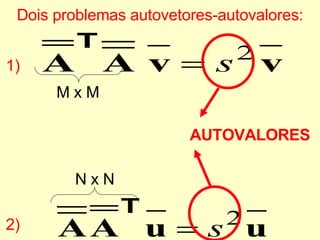
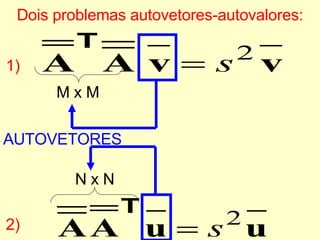
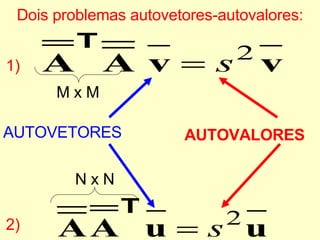
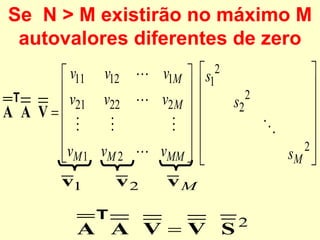
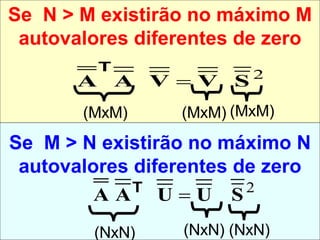
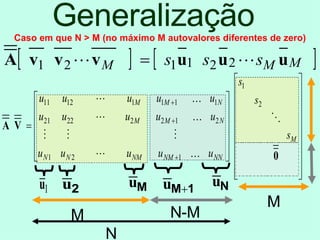
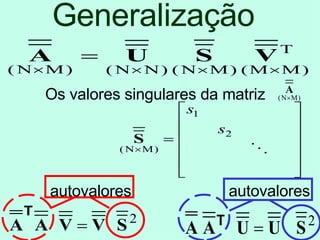
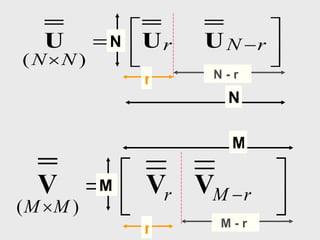
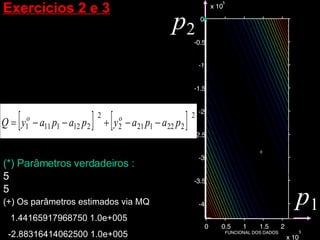
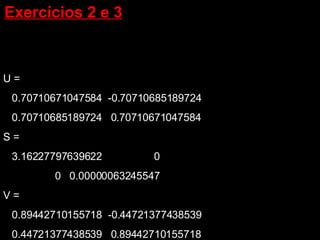
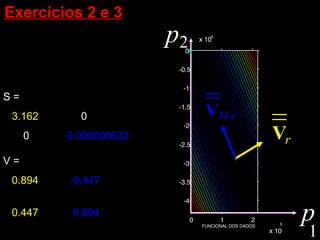
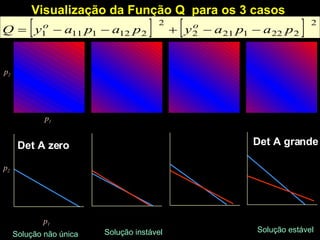
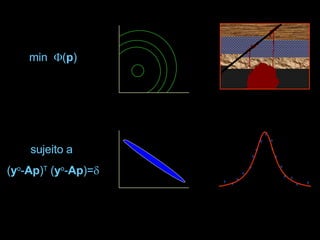
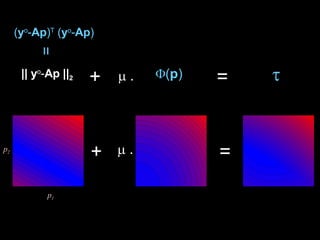
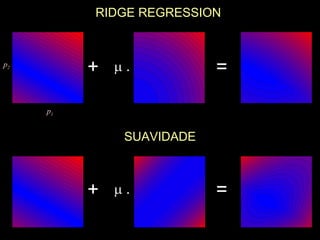
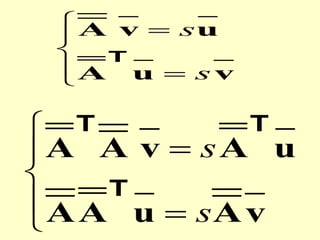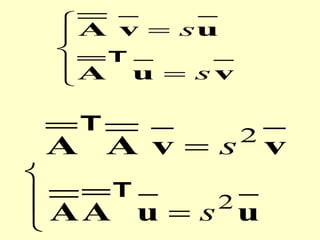O documento discute propriedades de autovalores e autovetores de sistemas lineares representados por matrizes. Explica que autovalores e autovetores permitem decompor uma matriz em espaços ortogonais e analisar propriedades como unicidade e estabilidade da solução do sistema linear. A decomposição em valores singulares é apresentada como forma de detectar problemas mal-postos no sistema.

1. Autovalorese Autovetores

2. O sistema linear do tipo: Matriz arbitrária ( N x N ) Não iremos resolver este sistema de equações lineares Estudaremos propriedades básicas deste sistema

3. (NxN) autovetor autovalor

4. Autovetor (eigenvector) Autovalor (eigenvalue)

5. Como achar os autovalores da matriz A (N x N) ?

6. EQUAÇÃO CARACTERÍSTICA DA MATRIZ Como achar os autovalores da matriz A (N x N) ? A

7. Interpretação Geométrica de autovalor e autovetor: Observação no. 1 Observação no. 2 Variável no.1 Variável no.2

8. Interpretação Geométrica de autovalor e autovetor: Variável no.1 Variável no.2 8 4 8 4 Observação no. 1 Observação no. 2 Variável no.2 Variável no.1 Observação no. 1 Observação no. 2

9. SOLUÇÃO DESTA EQUAÇÃO É: Como achar os autovalores da matriz A (N x N) ?

10. Como achar os autovetores da matriz A (N x N) ? Usamos o autovalor para achar o autovetor 1 Usamos o autovalor para achar o autovetor 2

11. A solução é: Usando o autovalor para achar o autovetor 1

12. A solução é: Usando o autovalor para achar o autovetor 1

13. Variável 1 Variável 2 Observação no.1 (4,8) Observação no.2 (8,4) 12 4 x 1 x 2

14. A forma elíptica indica a existência de um autovalor próximo a zero Mas o que significa autovalor próximo a zero ?

15. Interpretação Geométrica de autovalor e autovetor em dois casos extremos: caso (1) : Matriz não singular caso (2) : Matriz é singular

16. Qual é a interpretação Geométrica dos autovalores e autovetores neste dois casos extremos ? Qual o valor numérico dos autovalores nestes dois caso? caso (1) : Matriz não singular caso (2) : Matriz é singular

17. Variável 1 Variável 2 Observação no.1 (4,0) Observação no.2 (0,4) 4 4 Observações NÃO redundantes caso (1) :Matriz não singular caso (1) :Matriz não singular x 1 x 2

18. A forma circular indica a existência de autovalores idênticos Autovalores idênticos indica INDEPENDÊNCIA LINEAR do sistema

19. Variável 1 Variável 2 Observação no.1 (4,4) = Observação no.2 (4,4) 8 Observações Redundantes caso (2) :Matriz Singular caso (2) :Matriz Singular x 1 x 2

20. A forma LINEAR indica a existência de um autovalor zero AUTOVALOR ZERO indica DEPENDÊNCIA LINEAR do sistema DET da MATRIZ É ZERO NÃO UNICIDADE DA SOLUÇÃO

21. A forma elíptica fina indica a existência de um autovalor muito próximo a zero AUTOVALOR PRÓXIMO A ZERO indica uma QUASE DEPENDÊNCIA LINEAR do sistema DET da MATRIZ É próximo a ZERO SOLUÇÃO UNICIDADE porém INSTÁVEL

22. Como a Análise dos Autovalores da matriz associada com o sistema linear correspondente pode caracterizar um problema MAL-POSTO ?

23. AUTOVALOR ZERO: AUTOVALOR PRÓXIMO A ZERO: NÃO HÁ UNICIDADE DA SOLUÇÃO HÁ UNICIDADE DA SOLUÇÃO PORÉM A SOLUÇÃO É INSTÁVEL

24. NÃO HÁ UNICIDADE DA SOLUÇÃO DET =         A DET = 0 A Associação entre: Unicidade da solução, Determinante e Autovalor da matriz (NxN) do sistema linear A

25. HÁ UNICIDADE DA SOLUÇÃO porém a solução é instável DET =         A DET  0 A Associação entre: Estabilidade da solução, Determinante e Autovalor da matriz (NxN) do sistema linear A

26. Auto Sistema : Matriz arbitrária ( N x N )         Se existe N autovalores: Então existe um conjunto LI de N autovetores

27. Auto Sistema :         Se existe N autovalores: Então existe um conjunto LI de N autovetores

28. Auto Sistema :

29. Auto Sistema :

30. Auto Sistema :

31. Auto Sistema :         Se existe N autovalores: Então existe um conjunto LI de N autovetores Tal que :

32. Auto Sistema :

33. Auto Sistema : Matriz arbitrária ( N x N )     A existência de N autovalores: leva a existência de um conjunto LI de N autovetores que formam os vetores colunas de uma matriz que permite fazermos a seguinte decomposi ção

35. O Nosso sistema linear na geofísica: Matriz arbitrária ( N x M ) Não iremos resolver este sistema de equações lineares Estudaremos propriedades básicas deste sistema

36. Sistema linear principal: Sistema linear adjunto:

37. Combinando o Sistema linear Principal Dentro de um novo Sistema Linear: Com o Sistema Linear Adjunto:

38. Novo Sistema Linear: Sistema principal: Sistema adjunto:          T 0 A A 0 M N M N       p q       x y M N M N

39. A nova matriz é quadrada, logo podemos achar os autovalores e autovetores

40. problema de autovalor deslocado M N            v u (N + M x 1) w Pré x Pré x

43. Dois problemas autovetores-autovalores: AUTOVALORES M x M N x N 1) 2)

44. Dois problemas autovetores-autovalores: AUTOVETORES M x M N x N 1) 2)

45. Dois problemas autovetores-autovalores: M x M N x N 1) 2) AUTOVETORES AUTOVALORES

46. Dois problemas autovetores-autovalores: Existirão no máximo MIN(M,N) autovalores diferentes de zero M x M N x N 1) 2)

47. Se N > M existirão no máximo M autovalores diferentes de zero M x M

48. Presumindo-se, que N > M existirão no máximo M autovalores diferentes de zero

49. Presumindo-se, que N > M existirão no máximo M autovalores diferentes de zero

50. Se N > M existirão no máximo M autovalores diferentes de zero

51. Se M > N existirão no máximo N autovalores diferentes de zero N x N

52. Se M > N existirão no máximo N autovalores diferentes de zero

53. Se M > N existirão no máximo N autovalores diferentes de zero

54. Se M > N existirão no máximo N autovalores diferentes de zero

55. Se N > M existirão no máximo M autovalores diferentes de zero Se M > N existirão no máximo N autovalores diferentes de zero (MxM) (MxM) (MxM) (NxN) (NxN) (NxN)

56. Generalização Sem perda de generalidade, considere N > M. Então existirão no máximo M autovalores diferentes de zero

57. Generalização Caso em que N > M (no máximo M autovalores diferentes de zero)

58. Generalização Caso em que N > M (no máximo M autovalores diferentes de zero) N-M M N M

59. Generalização N M N

60. Generalização Quem são as matrizes Autovetores da Autovetores da

61. Generalização As matrizes são ortogonais As colunas da matriz são bases do espaço N (das observações) As colunas da matriz são bases do espaço M (dos parâmetros)

62. Generalização Pós multiplicando a equação por

63. Generalização Pós multiplicando a equação por DECOMPOSIÇÃO EM VALORES SINGULARES DA MATRIZ

64. Generalização autovalores autovalores Os valores singulares da matriz

65. A importância da Decomposição de uma Matriz em valores SINGULARES permite detectar se um problema é MAL-POSTO

66. Valor singular ZERO: Valor singular PRÓXIMO A ZERO: NÃO HÁ UNICIDADE DA SOLUÇÃO HÁ UNICIDADE DA SOLUÇÃO PORÉM A SOLUÇÃO É INSTÁVEL

67. Decomposição de uma Matriz em valores SINGULARES no caso em que r valores singulares são NULOS e r < (M e N) r r M - r N - r

68. N r N - r N M M r M - r

69. r valores singulares são NULOS r < (M e N)

70. Visualização do Espaço Iluminado e Espaço Não Iluminado (Espaço nulo) através da interpretação em duas dimensões Exercícios 2 e 3 O problema consiste em resolver o seguinte sistema linear de duas equações e duas incógnitas: 2 p(1) + p(2) = y(1) 2 p(1) + 1.000001 p(2) = y(2) O determinante desta matriz é quase zero (2 × 10 -6 ), caracterizando matematicamente um problema mal-posto devido a instabilidade da solução estimada .

71. Exercícios 2 e 3 Se estabeleço que os parâmetros verdadeiros são: 5 5 Dados Livres de ruido y(1) = 15.000000 y(2) = 15.000005 Dados COM de ruido y(1) = 15.415667732 y(2) = 15.127581767

72. Exercícios 2 e 3 Os parâmetros estimados via MQ é 1.44165917968750 1.0e+005 -2.88316414062500 1.0e+005

73. Exercícios 2 e 3 0 0.5 1 1.5 2 x 10 5 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 FUNCIONAL DOS DADOS (+) Os parâmetros estimados via MQ 1.44165917968750 1.0e+005 -2.88316414062500 1.0e+005 (*) Parâmetros verdadeiros : 5 5 0 * x 10 5 1 p 2 p

74. U = 0.70710671047584 -0.70710685189724 0.70710685189724 0.70710671047584 S = 3.16227797639622 0 0 0.00000063245547 V = 0.89442710155718 -0.44721377438539 0.44721377438539 0.89442710155718 Exercícios 2 e 3

75. Exercícios 2 e 3 x 10 5 x 10 5 0 1 2 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0 FUNCIONAL DOS DADOS 1 p V = 0.894 -0.447 0.447 0.894 S = 3.162 0 0 0.000000632 * 2 p r V M-r V

76. PREPARANDO OS SEUS CORAÇÕESINHOS PARA O EXERCÍCIO 3

77. Para garantir a existência, ao invés de resolver o sistema: minimiza-se: Exercício prático n.2 - parte 2 Exercício prático n.3

78. Para garantir a existência, ao invés de resolver o sistema: minimiza-se: Exercício prático n.2 - parte 2 Exercício prático n.3

79. p 1 p 1 p 2 p 2 Visualização da Função Q para os 3 casos Solução não única Det A zero Solução instável Solução estável Det A grande

80. 0.00 1.00 2.00 3.00 4.00 5.00

81. 0.00

83. min  ( p ) sujeito a ( y o - Ap ) T ( y o - Ap )= 

84. min  ( p ) sujeito a ( y o - Ap ) T ( y o - Ap ) =   = min  ( p )   Solução via multiplicadores de Lagrange ( y o - Ap ) T ( y o - Ap ) 

85.  ( p )  || y o - Ap || 2 p 1 p 2 + +  .  . = = ( y o - Ap ) T ( y o - Ap ) =

86. RIDGE REGRESSION +  . = SUAVIDADE p 1 p 2 +  . =