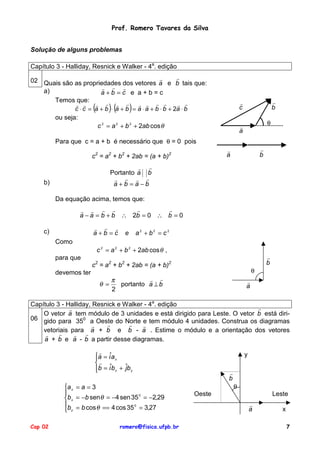
O documento fornece notas de aula sobre vetores e escalares, abordando conceitos fundamentais na física, como a definição de vetores e escalares, operações com vetores, e métodos geométricos e analíticos para representá-los. São discutidos conceitos como multiplicação de vetores, produto escalar e vetorial, bem como a resolução de problemas práticos relacionados a esses temas. A apresentação é acompanhada de exemplos relevantes e explicações sobre as propriedades dos vetores.