O documento aborda conceitos de cálculos de linha em análise matemática, incluindo parametrizações de curvas em R2 e R3, vetores tangentes, e integrais de linha em campos escalares e vetoriais. Exemplos e exercícios são fornecidos para praticar a representação e a parametrização de diversas curvas. Além disso, são discutidos os teoremas de Green e a classificação das curvas como fechadas ou abertas.

1. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Integrais de linha
An´alise Matem´atica II – C´alculo II
Sandra Gaspar Martins
2o Semestre 2013/14
Vers˜ao de 30 de Maio de 2014
sandra.martins@adm.isel.pt
1/49

2. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Equa¸c˜oes param´etricas da curva C
de R2
Defini¸c˜ao
Seja C uma curva/linha de R2 tal que
x = f (t)
y = g(t)
, t ∈ I = [a, b] ⊂ R,
com f e g fun¸c˜oes cont´ınuas em I. A t chama-se a vari´avel ou
parˆametro.
A orienta¸c˜ao da curva C corresponde ao sentido definido pelos
valores crescentes de t no intervalo I.
Ao ponto (x, y) correspondente a t = a chama-se origem ou
ponto de partida e ao correspondente a t = b chama-se
extremidade ou ponto de chegada da curva.
2/49

3. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Outra forma de descrever a curva C ´e utilizando fun¸c˜oes
vetoriais:
r : I = [a, b] −→ R2
t −→ r(t) = (f (t), g(t))
r(a) ´e a origem ou ponto de partida e
r(b) ´e a extremidade ou ponto de chegada de C.
Exemplo: Represente geometricamente a curva C:
r : [−1, 1] −→ R2
t −→ r(t) = (t, t2)
ou seja,
x = t
y = t2 , t ∈ I = [−1, 1]
ou seja,
r(t) = (t, t2
), t ∈ [−1, 1] 3/49

4. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios
Represente geometricamente as curvas:
1 r(t) = (t, t2), t ∈ [0, 2]
2 r(t) = (t, sin(t)), t ∈ [0, π]
3 r(t) = (t,
√
t), t ∈ [0, 9]
4 r(t) = (t, t + 3), t ∈ [0, 5]
5 r(t) = (t, t), t ∈ [0, 2]
6 r(t) = (t, −t), t ∈ [0, 2]
7 r(t) = (1 + 2t, 2 + t), t ∈ [0, 1]
8 r(t) = (t − 1, 3t + 2), t ∈ [0, 2]
9 r(t) = (t + 1, t2 + 3), t ∈ [0, 2]
10 r(t) = (|t|, |t|2), t ∈ [−2, 2]
11 r(t) = (|t|, |t| + 3), t ∈ [−3, 3]
4/49

5. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios
Represente geometricamente as curvas:
1 r(t) = (3 cos(t), 3 sin(t)), t ∈ [0, 2π]
2 r(t) = (2 cos(t), 4 sin(t)), t ∈ [0, π]
3 r(t) = (cos(t) − 2, sin(t) + 3), t ∈ [0, π
2 ]
4 r(t) = (cos(t), sin(t)), t ∈ [0, 2π]
5 r(t) = (5 cos(t), 4 sin(t)), t ∈ [π, 2π]
6 r(t) = (cos(t), sin(t)), t ∈ [−π, π
3 ]
7 r(t) = (cos(t) − 4, sin(t) + 2), t ∈ [−π
2 , 0]
8 r(t) = (2 cos(t), 2 sin(t)), t ∈ [0, 4π]
9 r(t) = (sin(t) − 1, cos(t) + 3), t ∈ [π
2 , 2π]
5/49

6. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Defini¸c˜ao
Uma parametriza¸c˜ao de um segmento de reta com origem em
A e extremidade em B, pode ser:
r(t) = A + t(AB), t ∈ [0, 1].
Defini¸c˜ao
Seja C uma curva dada pelo caminho r(t), t ∈ [a, b] com
origem em A = r(A) e extremidade em B = r(B). A curva −C
(com origem em B e extremidade em A) ´e dada pelo caminho
inverso de r, r∗, obt´em-se se r substituindo t por −t, ou seja,
r∗
(t) = r(−t), t ∈ [−b, −a]
.
Exemplo: Parametrize o segmento de reta de R2 que come¸ca
em (0,1) e termina em (2,3) e o caminho inverso.
6/49

7. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios I
Parametrize as seguintes curvas e as curvas inversas:
1 O segmento de reta que come¸ca em (1,2) e termina em
(-1,-3).
2 A parte da reta y = 2x para x ∈ [−2, 3].
3 A parte do gr´afico da fun¸c˜ao f (x) = ex2
− 1 para
x ∈ [0, 1].
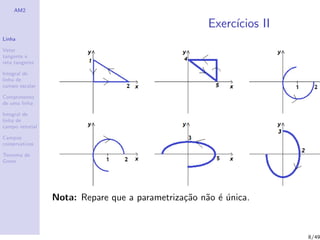
4 As linhas que se seguem:
7/49

8. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios II
Nota: Repare que a parametriza¸c˜ao n˜ao ´e ´unica.
8/49

9. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Equa¸c˜oes param´etricas da curva C
de R3
Defini¸c˜ao
Seja C uma curva/linha de R3 tal que



x = f (t)
y = g(t)
z = h(t)
, t ∈ I = [a, b] ⊂ R,
ou seja,
r : I = [a, b] −→ R3
t −→ r(t) = (f (t), g(t), h(t))
ou seja,
r(t) = (f (t), g(t), h(t)), t ∈ [a, b]
9/49

10. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios
Represente geometricamente as curvas:
1 r(t) = (0, 2, 2t), t ∈ [−1, 1]
2 r(t) = (0, t, 2t + 1), t ∈ [0, 3]
3 r(t) = (t, 5, t − 3), t ∈ [−2, 2]
4 r(t) = (0, |t|, |t|2 + 3), t ∈ [−3, 4]
5 r(t) = (cos(t), sin(t), 2), t ∈ [0, 2π]
6 H´elice circular:
r(t) = (cos(t), sin(t), t), t ∈ [0, 4π]
7 H´elice el´ıptica:
r(t) = (2 cos(t), 3 sin(t), t), t ∈ [0, 4π]
10/49

11. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios
Parametrize as linhas de R3 indicadas na figura seguinte que
representa o cilindro
{(x, y, z) ∈ R3
: x2
+ y2
= 9, 0 ≤ z ≤ 5}
11/49

12. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Classifica¸c˜ao de curvas
Defini¸c˜ao
Seja C uma curva dada por r(t), t ∈ [a, b].
A curva C diz-se fechada se a origem coincide com a
extremidade, ou seja, r(a) = r(b). Caso contr´ario a curva
diz-se aberta.
A curva C diz-se simples se n˜ao se intersecta a si pr´opria
(excluindo a origem e a extremidade).
12/49

13. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Vetor tangente e reta tangente
Defini¸c˜ao
Seja C uma curva de Rn dada por r(t), t ∈ [a, b].
Designa-se por vetor tangente `a curva C no ponto
P0 = r(t0) a derivada
r (t0) = lim
h→0
r(t0 + h) − r(t0)
h
, t0 ∈]a, b[
quando existe e ´e n˜ao nula.
A reta tangente `a curva em P0 = r(t0) ´e dada por:
(x, y, z) = r(t0) + tr (t0), t ∈ R
13/49

14. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
1 Considere o caminho, r(t), que leva de A = (1, 0) para
B = (−1, 0), ao longo de uma circunferˆencia de equa¸c˜ao
x2
+ y2
= 1
em sentido directo (anti-hor´ario). Determine a equa¸c˜ao da
reta tangente `a curva no ponto (0,1).
2 Considere o caminho, r(t), que leva de A = (1, 0) para
B = (0, 2), ao longo de uma elipse de equa¸c˜ao
x2
+
y2
4
= 1
em sentido directo (anti-hor´ario). Determine a equa¸c˜ao da
reta tangente `a curva no ponto correspondente a t = π
4 .
3 Determine a reta tangente `a curva representada pela
fun¸c˜ao
r(t) = (2 cos(t), 2 sin(t), t)
no ponto t0 = π
4 .
14/49

15. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Aplica¸c˜oes
Se r(t) der origem a uma curva que traduz o movimento de
um corpo ou part´ıcula, r (t) corresponder´a ao vetor
velocidade, ou seja,
v(t) = r (t).
O vetor acelera¸c˜ao ser´a
a(t) = v (t) = r (t).
Exemplo: Considere um objecto que se move ao longo de uma
curva C dada por
r(t) = (t − 2, t2
).
Determine os vetores velocidade e acelera¸c˜ao nos instantes
t = 0 e t = 1. Represente-os.
15/49

16. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Defini¸c˜ao
Uma curva C de Rn dada por r(t), t ∈ [a, b] diz-se regular
se a derivada r (t) existe e ´e cont´ınua (o que significa que
r(t) ∈ C1) e n˜ao nula em ]a, b[.
C ´e seccionalmente regular se se puder dividir num n´umero
finito de curvas regulares.
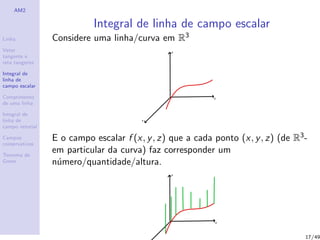
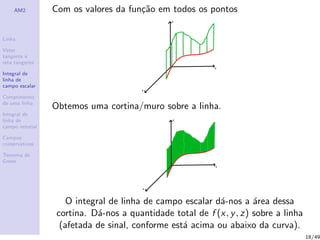
Nota: Se um caminho ´e regular, a curva por ele descrita n˜ao
apresenta bicos nem esquinas angulosas pois a derivada evolui
sem varia¸c˜oes bruscas de direc¸c˜ao ou sentido.
16/49

17. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Integral de linha de campo escalar
Considere uma linha/curva em R3
E o campo escalar f (x, y, z) que a cada ponto (x, y, z) (de R3-
em particular da curva) faz corresponder um
n´umero/quantidade/altura.
17/49

18. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Com os valores da fun¸c˜ao em todos os pontos
Obtemos uma cortina/muro sobre a linha.
O integral de linha de campo escalar d´a-nos a ´area dessa
cortina. D´a-nos a quantidade total de f (x, y, z) sobre a linha
(afetada de sinal, conforme est´a acima ou abaixo da curva).
18/49

19. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Por exemplo:
Se f (x, y, z) d´a a quantidade de ´agua que choveu no
ponto (x, y, z) durante um certo dia, o integral de f d´a a
quantidade total de ´agua que choveu sobre essa curva
nesse dia.
Se f (x, y, z) d´a temperatura no ponto (x, y, z) num dado
momento, podemos saber a temperatura m´edia sobre essa
linha dividindo o valor do integral pelo comprimento da
linha.
Se a linha for um arame com densidade dada pela fun¸c˜ao
ρ(x, y, z), o integral de ρ ao longo da linha d´a a massa
total do arame.
19/49

20. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
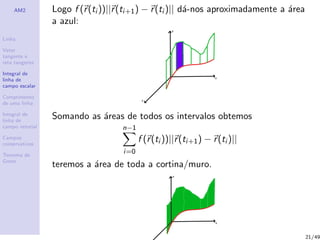
Como vamos obter este valor?
Seja C uma curva dada por r(t), t ∈ [a, b].
Dividindo o intervalo [a, b] em n intervalos [ti , ti+1],
i = 0, ..., n − 1.
Dividimos, tamb´em, a curva C em n intervalos [r(ti ), r(ti+1)].
||r(ti+1) − r(ti )|| d´a-nos aproximadamente o comprimento do
”intervalo i”da curva.
20/49

21. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Logo f (r(ti ))||r(ti+1) − r(ti )|| d´a-nos aproximadamente a ´area
a azul:
Somando as ´areas de todos os intervalos obtemos
n−1
i=0
f (r(ti ))||r(ti+1) − r(ti )||
teremos a ´area de toda a cortina/muro.
21/49

22. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Repare que ||r(ti+1)−r(ti )||
∆t ≈ ||r (ti )|| pelo que a ´area total pode
ser escrita como
n−1
i=0
f (r(ti ))||r (ti )|| ∆t
Passando ao limite
lim
n→+∞
n−1
i=0
f (r(ti ))||r (ti )|| ∆t
obtemos
b
a
f (r(t)) r (t) dt
que ´e o valor exato da ´area da cortina, ´e potanto, o que
designamos por integral de linha de campo escalar.
22/49

23. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Defini¸c˜ao
Seja C uma curva dada por r(t), t ∈ [a, b].
Seja f : Df ⊂ Rn −→ R um campo escalar cont´ınuo cujo
dom´ınio Df contem todos os pontos da curva C
Chamamos integral de linha do campo escalar f ao longo da
curva C ao integral
C
f ds =
b
a
f (r(t)) r (t) dt
Notas:
Este integral n˜ao depende da parametriza¸c˜ao escolhida
para C.
http://www.personal.psu.edu/dpl14/java/calculus/lineintegral.html
23/49

24. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Propriedades
Propriedades dos integrais de linha de campos escalares:
Seja f e g campos escalares cont´ınuos com Df , Dg ⊂ Rn e
C curva regular totalmente contida em Df ∩ Dg .
C1 e C2 curvas regulares totalmente contidas em Df .
−C a curva inversa da curva C (totalmente contidas em Df ).
α, β ∈ R.
1
−C
f ds =
C
f ds
2
C
αf + βg ds = α
C
f ds + β
C
g ds
3
C1∪C2
f ds =
C1
f ds +
C2
f ds
Aplica¸c˜oes: A massa de uma linha C com densidade dada pela
fun¸c˜ao ρ(x, y, x) ´e C ρ ds
24/49

25. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios I
1 Calcule C f ds onde f (x, y) = x e C ´e a linha da figura:
2 Calcule C y ds onde C ´e a meia circunferˆencia de raio 2
centrada na origem percorrida no sentido anti-hor´ario
desde o ponto (2,0) at´e ao ponto (-2,0). (R: 8)
3 Sabendo que a densidade de um fio ´e dada por
ρ(x, y) = 2
√
x − y onde C tem a forma de um segmento
de reta com origem em (0,0) e extremidade em (1,1).
Calcule a massa desse fio. (R:5
√
2
6 )
25/49

26. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios II
4 Calcule C x + z ds onde C ´e o segmento de reta que tem
origem em (0,2,3) e termina em (2,1,0). (R:5
√
14
2 )
5 Calcule C x + y + z ds onde C ´e a linha de equa¸c˜ao
param´etrica 


x = cos(t)
y = sin(t)
z = t
entre os pontos (1,0,0) e (1,0,2π). R: 2
√
2π2
26/49

27. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Comprimento de uma linha
O integral de linha do campo escalar f (x, y, z) = 1 d´a o
comprimento da linha, ou seja:
Defini¸c˜ao
Seja C uma curva dada por r(t), t ∈ [a, b].
Chamamos comprimento da linha/curva C com origem em
A = r(a) e extremidade B = r(b) ao integral
lC =
b
a
r (t) dta
a
Este integral n˜ao depende da parametriza¸c˜ao escolhida para C.
27/49

28. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios
1 Prove que o per´ımetro de uma circunferˆencia de raio R ´e
2πR.
2 Determine k de modo que o comprimento da reta
y = −2x + 1 entre 0 e k seja 2.
3 Considere
r(t) = 4 sin(t)e1 + 3te2 + 4 cos(t)e3, t ∈ [0, π]
Esboce a curva e calcule o seu comprimento. (R : 5π)
4 Determine o comprimento da curva C de equa¸c˜oes
x = et cos(t)
y = et sin(t)
, t ∈ 0,
π
2
5 Determine o comprimento do arco de curva dado por



x = aet cos(t)
y = aet sin(t)
z = aet
desde (a, o, a) at´e (−aeπ, 0, aeπ). R:
√
3a(eπ − 1) 28/49

29. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Defini¸c˜ao
Seja C uma curva dada por r(t) = (x(t), y(t), z(t)), t ∈ [a, b].
Seja f : Df
⊂ Rn −→ R3 f = (f1, f2, f3) um campo vetorial
cont´ınuo cujo dom´ınio Df
contem todos os pontos da curva C.
Chamamos integral de linha do campo vetorial f ao longo
da curva C ao integral
C
f · dr =
b
a
f (r(t)) · r (t) dt =
b
a
f1 dx + f2 dy + f3 dz
Notas:
Se admitirmos que f representa um campo de for¸cas, o
integral da fun¸c˜ao vetorial f ao longo da linha C
representa o trabalho realizado por f para deslocar uma
part´ıcula ao longo da linha C .
Este integral n˜ao depende da parametriza¸c˜ao escolhida
para C.
http://mathinsight.org/line_integral_vector_field_
introduction
29/49

30. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Propriedades
Propriedades dos integrais de linha de campos vetoriais:
Seja f e g campos escalares cont´ınuos com Df
, Dg ⊂ Rn e
C curva regular totalmente contida em Df
∩ Dg .
C1 e C2 curvas regulares totalmente contidas em Df
.
−C a curva inversa da curva C (totalmente contidas em Df
).
α, β ∈ R.
1
−C
f · dr = −
C
f · dr
2
C
αf + βg · dr = α
C
f · dr + β
C
g · dr
3
C1∪C2
f · dr =
C1
f · dr +
C2
f · dr
30/49

31. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios:
1 Calcule o trabalho realizado pela for¸ca
f (x, y) = (x2 − 2xy, 2xy + y2) ao longo da linha y = x2
desde (0,0) at´e (3,9). R:405.9
2 Calcule o trabalho realizado pela for¸ca
f (x, y) = (1 + xy, x − y) no deslocamento do seu ponto
de aplica¸c˜ao ao longo da linha fechada definida por y = x,
y = −1, x = 0 e x = 2 no sentido hor´ario. R:−2
3
3 Calcule o trabalho realizado pela for¸ca f (x, y) = (y, x) ao
deslocar uma part´ıcula desde (0,0) at´e (1,1) ao longo das
linhas
1 y = x
2 y = x2
3 y = x3
R:1
31/49

32. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Interpreta¸c˜ao
Imagine que est´a a remar num rio com alguma corrente. `As
vezes est´a a trabalhar contra a corrente, outras vezes est´a a
movimentar-se gra¸cas a ela. No final tem a sensa¸c˜ao de saber
se, em geral, foi ajudado ou prejudicado pela corrente.
O integral de linha mede o grau em que uma curva num campo
de vectores est´a, em geral, a ir com o campo de vectores ou
contra ele.
Lembre-se que para quaisquer dois vetores u e v o produto
interno u · v ´e positivo se u e v apontam aproximadamente na
mesma direc¸c˜ao (isto ´e, se o ˆangulo entre eles ´e inferior a π
2 ).
O produto interno ´e zero se u ´e perpendicular a v e ´e negativo,
se eles apontam aproximadamente em direc¸c˜oes opostas (isto
´e, se o ˆangulo entre eles ´e maior do que π
2 ).
32/49

33. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
O integral de linha de f adiciona o produto interno de f e ∆r
ao longo do caminho.
Se ||f || ´e constante, o integral de linha d´a um n´umero positivo
se f (maioritariamente) apontar na mesma dire¸c˜ao que C, e um
n´umero negativo se f (maioritariamente) apontar na dire¸c˜ao
oposta `a de C. O integral de linha ´e zero se f ´e perpendicular
ao percurso em todos os pontos, ou se as contribui¸c˜oes
positivas e negativas se anularem.
Em geral, o integral de linha de um campo vectorial f ao longo
de uma curva C mede at´e que ponto C vai com f ou contra f .
(De: Hughes-Hallett, Calculus)
33/49

34. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcio
Considere o campo vetorial f e as curvas C1, C2, C3, e C4
apresentadas na figura. As curvas C1 e C3 tˆem o mesmo
comprimento. Quais dos seguintes integrais s˜ao positivos? E
negativos? Ordene-os de forma crescente.
Ci
f · dr i = 1, 2, 3, 4
R: C4, C1, C3, C2
34/49

35. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcio
Qual o sinal do integral dos seguintes campos vetoriais nas
respetivas linhas?
R: 1.neg 2.pos 3.zero 4.pos 5.zero
35/49

36. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Campos conservativos
Imagine que pretende transportar um sof´a de um r´es-do-ch˜ao
para o 1o andar. Ter´a que ”lutar”contra a gravidade. A for¸ca
que vai ser feita ´e a mesma quer v´a pelo elevador quer v´a pelas
escadas. Vamos modelar este problema e confirm´a-lo:
A for¸ca da gravidade pode ser modelada por
f (x, y, z) = (0, 0, −9.8). Vamos modelar o caminho do
elevador pelo segmento de reta entre (0,0,0) e (0,0,2). O
primeiro lance de escadas pelo segmento de reta que come¸ca
em (0,0,0) e termina em (0,1,1) e o segundo pelo segmento de
reta que come¸ca em (0,1,1) e termina em (0,0,2).
Calcule o trabalho realizado por esta for¸ca ao longo dos dois
caminhos.
36/49

37. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Nesta sec¸c˜ao consideremos apenas campos vetoriais
f = (f1, f2, ..., fn) cujas componentes sejam cont´ınuas num
conjunto aberto, simplesmente conexo.
Defini¸c˜ao
f : Rn −→ Rn ´e um campo conservativo (ou campo
gradiente) se existe ϕ : Rn −→ R
f = ϕ(x),
ou seja,
(f1, f2, ..., fn) =
∂ϕ
∂x1
,
∂ϕ
∂x2
, ...,
∂ϕ
∂xn
`A fun¸c˜ao ϕ chama-se a fun¸c˜ao potencial geradora de f .
37/49

38. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Vejamos se f (x, y) = (2xy3 + 1, 3x2y2 + 12y3) ´e conservativo.
Ou seja, vamos procurar
ϕ(x, y) : f (x, y) = ϕ(x, y) = ∂ϕ
∂x , ∂ϕ
∂y



∂ϕ
∂x = 2xy3 + 1 ⇒ ϕ(x, y) = x2y3 + x + C(y)
⇓
∂ϕ
∂y = 3x2y2 + 12y3 ∂ϕ
∂y = 3x2y2 + 0 + C (y)
comparando:
C (y) = 12y2
C(y) = 4y3
+ k
portanto
ϕ(x, y) = x2
y3
+ x + 4y3
+ k, k ∈ R
Ou seja, f ´e conservativo.
38/49

39. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios:
Verifique se os seguintes campos vetoriais s˜ao conservativos:
1 f (x, y) = (2xy3, 3x2y2 + 2y)
2 f (x, y) = (2x + 2y, 2x − 3y2)
3 f (x, y) = (cos(y) − 2y cos(x), −x sin(y) − 2sin(x))
4 f (x, y, z) = (2xyz, x2z + 2, x2y + 3z2)
5 f (x, y) = (yexy , xexy )
6 f (x, y) = (2xy5, x5y2)
39/49

40. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Teorema
Seja C uma curva dada por r(t), t ∈ [a, b], portanto com
origem A = r(a) e extremidade B = r(b). Se um campo
vetorial f ´e conservativo, isto ´e, f = ϕ ent˜ao
w =
C
f · dr = ϕ(B) − ϕ(A)
ou seja, o trabalho realizado por f ´e independente do
caminho.
Nota: Quando o campo ´e conservativo o trabalho ao longo de
uma linha fechada ´e 0.
40/49

41. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Demonstra¸c˜ao:
w =
C
f · dr
=
b
a
f (r(t)) · r (t) dt
=
b
a
ϕ(r(t)) · r (t) dt
=
b
a
dϕ(r(t))
dt
dt
= ϕ(r(b)) − ϕ(r(a))
= ϕ(B) − ϕ(A)
41/49

42. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios
1 Calcule o valor do integral C f · dr onde
f (x, y) = (2xy − y4 + 3, x2 − 4xy3) sendo C um caminho
qualquer que une os pontos (1,0) a (2,1).
2 Calcule o trabalho de f (x, y, z) = (yzexyz, xzexyz, xyexyz)
ao longo da espiral descrita pelo caminho
r(t) = (5 cos(t),
√
t, 5 sin(t)) com t ∈ [0, 4π].
3 Considere o campo vetorial F(x, y) = (x2 + y2, αxy), com
α ∈ R.
1 Determine o valor de α para o qual F ´e um campo
gradiente.
2 Para o valor de α determinado na al´ınea anterior calcule o
trabalho realizado pelo campo F ao longo do caminho
γ(t) = (t, et2
−1
), t ∈ [0, 1].
42/49

43. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Teorema
Seja f : Rn −→ Rn.
f ´e conservativo, se e s´o se,
Jf
= JT
f
.
Ou seja, sse a matriz Jacobiana ´e sim´etrica.
Nota: No caso de f : R2 −→ R2.
f ´e conservativo, se e s´o se,
∂f1
∂y
=
∂f2
∂x
.
43/49

44. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios:
Confirmemos agora de outra forma se s˜ao, ou n˜ao,
conservativos os campos vetoriais que estud´amos atr´as:
1 f (x, y) = (2xy3, 3x2y2 + 2y)
2 f (x, y) = (2x + 2y, 2x − 3y2)
3 f (x, y) = (cos(y) − 2y cos(x), −x sin(y) − 2sin(x))
4 f (x, y, z) = (2xyz, x2z + 2, x2y + 3z2)
5 f (x, y) = (yexy , xexy )
6 f (x, y) = (2xy5, x5y2)
44/49

45. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Teorema de Green
Seja C uma curva dada por r(t), t ∈ [a, b], fechada, simples,
seccionalmente de classe C1, orientada no sentido positivo1
cujo interior ´e a regi˜ao A.
Seja f : Df
⊂ R2 −→ R2, f = (f1, f2) um campo vetorial de
classe C1 cujo dom´ınio Df
contem todos os pontos da curva C
e do seu interior, A.
Ent˜ao
C
f · dr =
A
∂f2
∂x
−
∂f1
∂y
dx dy.
1
deixando `a esquerda os pontos do interior de C.
45/49

46. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios I
1 Verifique o teorema de Green para a fun¸c˜ao
f (x, y) = (2y, x + 3) e a seguinte regi˜ao sombreada:
R: −π
2
2 Use o teorema de Green para a confirmar que a ´area de
um c´ırculo de raio R ´e πR2.
3 Verifique o teorema de Green para a fun¸c˜ao
F(x, y) = 2xye1 + (x − y)e2 para a regi˜ao de R2 em que
0 ≤ y ≤ x + 2 e x2 + y2 ≤ 4. R: π − 2
3
46/49

47. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios II
4 Utilize o teorema de Green para calcular o trabalho
realizado pelo campo de for¸cas F(x, y) = (1 + y, y + x) ao
deslocar uma part´ıcula ao longo da fronteira de R
percorrida no sentido positivo em que
R = (x, y) ∈ R2
: 1 ≤ x2
+ y2
< 4, y ≤ x, x ≥ 0 .
5 Utilize o teorema de Green para calcular o valor de
D yex+y dx dy com F(x, y) = (yex+y , ex+y ) e
D = (x, y) ∈ R2
: 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 .
47/49

48. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Exerc´ıcios III
6 * Considere a linha
L = (x, y) ∈ R2
: x2
+ y2
= 1, x ≤ 0
”percorrida de baixo para cima”e o campo vetorial
F(x, y) = (xy2, xy). Use o Teorema de Green para
calcular o trabalho realizado por F ao longo de L.
R: 0
7 Considere a regi˜ao
R = (x, y) ∈ R2
: x2
+ y2
≤ 1, y ≥ x2
− 1 .
Calcule a ´area de R sem calcular integrais duplos.
Nota:
P(sin2
(x)) = x
2 − sin(2x)
4
P(cos2(x)) = x
2 + sin(2x)
4
48/49

49. AM2
Linha
Vetor
tangente e
reta tangente
Integral de
linha de
campo escalar
Comprimento
de uma linha
Integral de
linha de
campo vetorial
Campos
conservativos
Teorema de
Green
Autora:
Sandra Gaspar Martins
Com base no trabalho de:
Nuno David Lopes
e
Cristina Janu´ario
49/49