GCET149_Slides aula 14.pdf

Cálculo Diferencial e Integral IV
Universidade Federal do Recôncavo da Bahia
01/06/2022
Paulo Henrique Ribeiro do Nascimento

Integrais Curvilíneas de Campos Vetoriais
Definição
2 CETEC Paulo Henrique Ribeiro do Nascimento 01/06/2022

Definição
Sejam γ(t) = (x(t), y(t)) (ou γ(t) = (x(t), y(t), z(t))) definida em I ⊂ R uma curva
regular e ⃗
F um campo contínuo cujo domínio contém o traço desta curva.

Definição
regular e ⃗
Efetuemos uma partição de I = [a, b] em n − 1 subintervalos de comprimentos ∆ti =
ti+1 − ti, 1 ≤ i ≤ n, a qual induz uma partição do traço de γ em n − 1 sub-arcos de
comprimentos ∆si, 1 ≤ i ≤ n.

Definição
regular e ⃗
Efetuemos uma partição de I = [a, b] em n − 1 subintervalos de comprimentos ∆ti =
ti+1 − ti, 1 ≤ i ≤ n, a qual induz uma partição do traço de γ em n − 1 sub-arcos de
comprimentos ∆si, 1 ≤ i ≤ n.
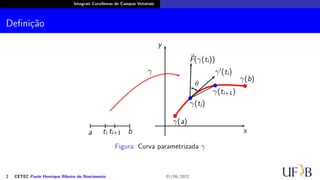
Em t = ti, temos que:
⃗
F(γ(ti)) · γ′
(ti) = |⃗
F(γ(ti))||γ′
(ti)| cos(θ),
em que θ é o ângulo formado pelos vetores ⃗
F(γ(ti)) e γ′(ti).

Definição
a b
ti ti+1
γ
x
y
γ(a)
γ(b)
γ(ti+1)
γ(ti)
⃗
F(γ(ti))
γ′(ti)
θ
b
b
b
b
Figura: Curva parametrizada γ

Definição
Dessa forma, como γ é regular,
⃗
F(γ(ti)) ·
γ′(ti)
|γ′(ti)|
= |⃗
F(γ(ti))| cos(θ),

Definição
⃗
F(γ(ti)) ·
γ′(ti)
|γ′(ti)|
= |⃗
F(γ(ti))| cos(θ),
sendo que
⃗
F(γ(ti)) ·
γ′(ti)
|γ′(ti)|
∆si = |⃗
F(γ(ti))| cos(θ)∆si = Wi.

Definição
⃗
F(γ(ti)) ·
γ′(ti)
|γ′(ti)|
= |⃗
F(γ(ti))| cos(θ),
sendo que
⃗
F(γ(ti)) ·
γ′(ti)
|γ′(ti)|
∆si = |⃗
Observe que como ∆si é uma boa aproximação para o comprimento do segmento que
une os pontos γ(ti) e γ(ti+1) e;

Definição
⃗
F(γ(ti)) ·
γ′(ti)
|γ′(ti)|
= |⃗
F(γ(ti))| cos(θ),
sendo que
⃗
F(γ(ti)) ·
γ′(ti)
|γ′(ti)|
∆si = |⃗
Observe que como ∆si é uma boa aproximação para o comprimento do segmento que une
os pontos γ(ti) e γ(ti+1) e; por ser ⃗
F contínua e, portanto, aproximadamente constante
para uma muito pequena variação de t, o segundo membro desta última equação é uma
aproximação para o trabalho Wi de uma partícula sujeita a ação de um campo de forças
⃗
F ao se deslocar de γ(ti) a γ(ti+1).

Definição
Fazendo i variar de 1 a n, sua soma é dada por:

Definição
n
∑
i=1
⃗
F(γ(ti)) ·
γ′(ti)
|γ′(ti)|
∆si =
n
∑
i=1
|⃗
F(γ(ti))| cos(θ)∆si
=
n
∑
i=1
Wi ≈ W,

Definição
n
∑
i=1
⃗
F(γ(ti)) ·
γ′(ti)
|γ′(ti)|
∆si =
n
∑
i=1
|⃗
=
n
∑
i=1
Wi ≈ W,
em que W é o trabalho de uma partícula sujeita ao campo de forças ⃗
F ao se deslocar
de γ(a) a γ(b).

Definição
O limite da soma, ao fazermos os valores de n crescerem indefinidamente, é:

Definição
lim
n→∞
n
∑
i=1
⃗
F(γ(ti)) ·
γ′(ti)
|γ′(ti)|
∆si = lim
n→∞
n
∑
i=1
⃗
F(γ(ti)) · γ′
(ti)∆ti,

Definição
lim
n→∞
n
∑
i=1
⃗
F(γ(ti)) ·
γ′(ti)
|γ′(ti)|
∆si = lim
n→∞
n
∑
i=1
⃗
F(γ(ti)) · γ′
(ti)∆ti,
ou seja,

Definição
lim
n→∞
n
∑
i=1
⃗
F(γ(ti)) ·
γ′(ti)
|γ′(ti)|
∆si = lim
n→∞
n
∑
i=1
⃗
F(γ(ti)) · γ′
(ti)∆ti,
ou seja,
∫
γ
⃗
F(γ(t)) · ⃗
ν ds =
∫ b
a
⃗
F(γ(t)) · γ′
(t) dt,

Definição
lim
n→∞
n
∑
i=1
⃗
F(γ(ti)) ·
γ′(ti)
|γ′(ti)|
∆si = lim
n→∞
n
∑
i=1
⃗
F(γ(ti)) · γ′
(ti)∆ti,
ou seja,
∫
γ
⃗
F(γ(t)) · ⃗
ν ds =
∫ b
a
⃗
F(γ(t)) · γ′
(t) dt,
a integral de linha de ⃗
F ao longo de γ,

Definição
No caso R2, para ⃗
F(x, y) = P(x, y)
⃗
i + Q(x, y)⃗
j integrável e γ(t) = x(t)
⃗
i + y(t)⃗
j regular,
contida no domínio de ⃗
F, temos:

Definição
F(x, y) = P(x, y)
⃗
i + Q(x, y)⃗
⃗
i + y(t)⃗
j regular,
F, temos:
∫ b
a
[P x′
(t) + Q y′
(t)] dt =
∫ b
a
P dx + Q dy.
usando a notação dx = x′(t) dt e dy = y′(t) dt.

Definição
F(x, y) = P(x, y)
⃗
i + Q(x, y)⃗
⃗
i + y(t)⃗
j regular,
F, temos:
∫ b
a
[P x′
(t) + Q y′
(t)] dt =
∫ b
a
P dx + Q dy.
usando a notação dx = x′(t) dt e dy = y′(t) dt.
Assim, ∫
γ
⃗
F · d⃗
s =
∫ b
a
P dx + Q dy.

Definição
F(x, y, z) = P(x, y, z)
⃗
i + Q(x, y, z)⃗
j + R(x, y, z)⃗
k integrável e γ(t) =
x(t)
⃗
i + y(t)⃗
j + z(t)⃗
k regular, contida no domínio de ⃗
F, temos:

Definição
F(x, y, z) = P(x, y, z)
⃗
i + Q(x, y, z)⃗
j + R(x, y, z)⃗
x(t)
⃗
i + y(t)⃗
j + z(t)⃗
F, temos:
∫ b
a
[P x′
(t) + Q y′
(t) + R z′
(t)] dt. =
∫ b
a
P dx + Q dy + R dz,
usando a notação dx = x′(t) dt, dy = y′(t) dt e dz = z′(t) dt.

Definição
F(x, y, z) = P(x, y, z)
⃗
i + Q(x, y, z)⃗
j + R(x, y, z)⃗
x(t)
⃗
i + y(t)⃗
j + z(t)⃗
F, temos:
∫ b
a
[P x′
(t) + Q y′
(t) + R z′
(t)] dt. =
∫ b
a
P dx + Q dy + R dz,
usando a notação dx = x′(t) dt, dy = y′(t) dt e dz = z′(t) dt. Assim,
∫
γ
⃗
F · d⃗
s =
∫ b
a
P dx + Q dy + R dz.

Definição
F(x, y, z) = P(x, y, z)
⃗
i + Q(x, y, z)⃗
j + R(x, y, z)⃗
x(t)
⃗
i + y(t)⃗
j + z(t)⃗
F, temos:
∫ b
a
[P x′
(t) + Q y′
(t) + R z′
(t)] dt. =
∫ b
a
P dx + Q dy + R dz,
usando a notação dx = x′(t) dt, dy = y′(t) dt e dz = z′(t) dt. Assim,
∫
γ
⃗
F · d⃗
s =
∫ b
a
P dx + Q dy + R dz.
Não é difícil provar que a integral de linha não depende da particular parametrização da
curva, desde que não se inverta a sua orientação.

Referências
G. B. Arfken and H. J. Weber.
Mathematical methods for physicists.
American Association of Physics Teachers, 1999.
C. Bouvier, A. Benoit, A. Caplier, and P.-Y. Coulon.
Open or closed mouth state detection: Static supervised classification based on log-polar signature.
In Proceedings of the 10th International Conference on Advanced Concepts for Intelligent Vision Systems, volume 5259, pages 1093–1102,
October 2008.
G. D. Greenwade.
The Comprehensive Tex Archive Network (CTAN).
TUGBoat, 14(3):342–351, 1993.
J. J. O’CONNOR and E. F. ROBERTSON.
Friedrich Wilhelm Bessel, 1997.
E. Tola, V. Lepetit, and P. Fua.
Daisy: An eﬀicient dense descriptor applied to wide-baseline stereo.
IEEE transactions on pattern analysis and machine intelligence, 32(5):815–830, 2010.

GCET149_Slides aula 14.pdf

Mais conteúdo relacionado

Semelhante a GCET149_Slides aula 14.pdf

Mais de IntegrePrograma

Último

GCET149_Slides aula 14.pdf