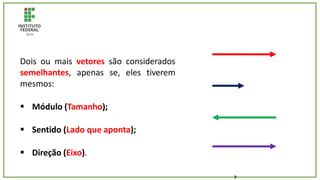
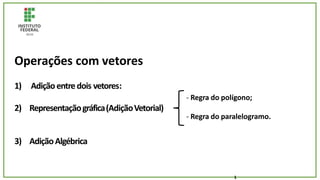
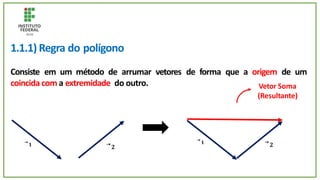
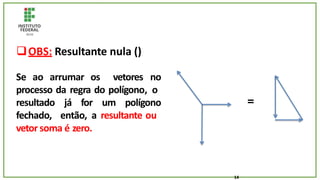
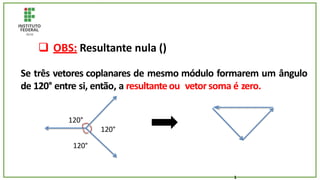
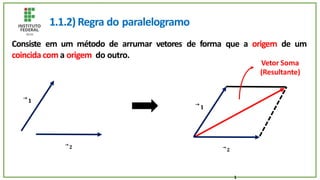
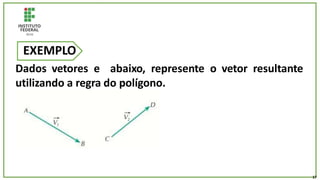
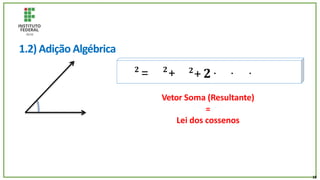
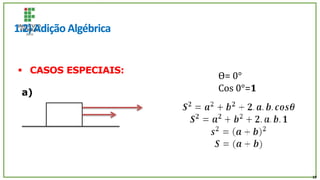
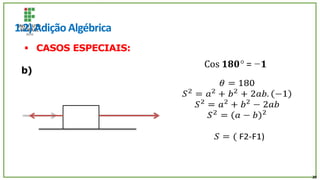
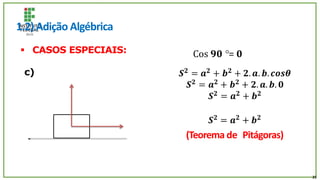
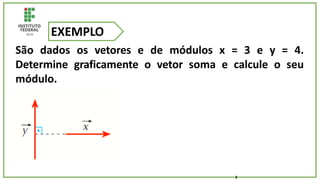
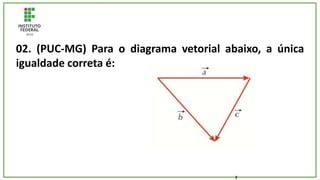
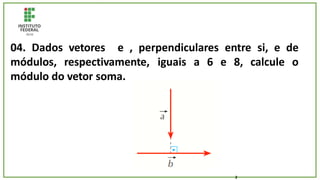
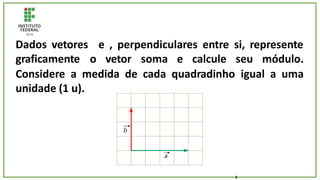
O documento trata de um corpo que é abandonado de uma torre e cai livremente por dois segundos. Com base nisso, pede-se para calcular: 1) A velocidade com que o corpo atinge o solo considerando a gravidade de 9,8 m/s2 2) A velocidade com que o corpo atingiria o solo na Lua, onde a gravidade é de 1,6 m/s2

2. Joãozinho abandona do alto de uma torre um corpo a
partir do repouso. Durante a queda livre, com g
constante, ele observa que nos dois primeiros segundos o
corpo chega ao solo. Sabendo que a aceleração da
gravidade local é 9,8 m/s², determine:
a) A velocidade que o corpo chega o solo.
b)A velocidade que o corpo teria ao chegar ao solo, caso
estivesse na Lua (gLua = 1,6 m/s²).
2

3. VETORES
 Caracterização de um vetor
 Grandezas vetoriais e grandezas escalares
 Operações com vetores
-
-
Representação gráfica
Operações algébricas

4. Vetores
Definição
VETOR é o ente matemático caracterizado por um conjunto de
características, sendo elas: comprimento (módulo), direção e o sentido.
4

5. A
B
a
a = B - A
Um VETOR pode ser simbolizado:
Por uma seta;



Dois extremos
representados
por letras
maiúsculas;
Uma letra minúscula
com uma
pequena seta em cima.
Origem
Extremidade
5

6.  MÓDULO: TAMANHO do vetor;
 DIREÇÃO: POSIÇÃO na qual o vetor se
encontra (vertical, horizontal ou
oblíqua);
 SENTIDO: Para onde o vetor APONTA.

7. Dois ou mais vetores são considerados
semelhantes, apenas se, eles tiverem
mesmos:
 Módulo (Tamanho);
 Sentido (Lado que aponta);
 Direção (Eixo).
7

8. 8
 GRANDEZAS ESCALARES são grandezas que ficam perfeitamente
definidas quando conhecemos seu valor numérico e a correspondente
unidade. Ex: massa, temperatura, tempo.
 GRANDEZAS VETORIAIS são grandezas necessitam, além do valor
numérico e da unidade, de direção e de sentido. Ex: Velocidade,
Deslocamento, Força.

9. Vetores
Grandezas
GRANDEZA VETORIAL GRANDEZA ESCALAR
9

10. São grandezas vetoriais:
a) tempo, deslocamento e força.
b) força, velocidade e aceleração.
c) tempo, temperatura e volume.
d) temperatura, velocidade e volume.
e) volume, deslocamento e massa.
EXEMPLO
1

11. (Unitau-SP) Uma grandeza vetorial fica perfeitamente
definida quando dela se conhecem:
a) valor numérico, desvio e unidade.
b) valor numérico, desvio, unidade e direção.
c) valor numérico, desvio, unidade e sentido.
d) valor numérico, unidade, direção e sentido.
e) desvio, direção, sentido e unidade.
EXEMPLO
1

12. Operações com vetores
1) Adiçãoentredois vetores:
2) Representaçãográfica(AdiçãoVetorial)
3) AdiçãoAlgébrica
- Regra do polígono;
- Regra do paralelogramo.
1

13. 1.1.1) Regra do polígono
Consiste em um método de arrumar vetores de forma que a origem de um
coincida com a extremidade do outro.
⃗𝟏
⃗𝟐
⃗𝟏
⃗𝟐
Vetor Soma
(Resultante)

14. OBS: Resultante nula ()
Se ao arrumar os vetores no
processo da regra do polígono, o
resultado já for um polígono
fechado, então, a resultante ou
vetor soma é zero.
=
14

15. 120°
120°
120°
 OBS: Resultante nula ()
Se três vetores coplanares de mesmo módulo formarem um ângulo
de 120° entre si, então, a resultanteou vetor soma é zero.
1

16. 1.1.2) Regra do paralelogramo
⃗𝟐
⃗𝟏
⃗𝟐
⃗𝟏
Consiste em um método de arrumar vetores de forma que a origem de um
coincida com a origem do outro.
Vetor Soma
(Resultante)
1

17. EXEMPLO
Dados vetores e abaixo, represente o vetor resultante
utilizando a regra do polígono.
17

18. 1.2) Adição Algébrica
𝟐
= 𝟐
+
18
𝟐
+ 𝟐∙ ∙ ∙
Vetor Soma (Resultante)
=
Lei dos cossenos

19. 1.2) Adição Algébrica
 CASOS ESPECIAIS:
a)
ϴ= 0°
Cos 0°=𝟏
19

20. 1.2) Adição Algébrica
 CASOS ESPECIAIS:
b)
Cos 𝟏𝟖𝟎° = −𝟏
20

21. 1.2) Adição Algébrica
(Teorema de Pitágoras)
21
 CASOS ESPECIAIS:
c)
Cos 𝟗𝟎 °= 𝟎

22. A figura a seguir representa diferentes vetores com seus
respectivos módulos. Utilizando a regra do polígono,
represente o vetor resultante e determine seu módulo.
a)
b)
EXEMPLO
23

23. São dados os vetores e de módulos x = 3 e y = 4.
Determine graficamente o vetor soma e calcule o seu
módulo.
EXEMPLO
2

24. 01. São grandezas escalares:
a) tempo, deslocamento e força.
b) força, velocidade e aceleração.
c) tempo, temperatura e massa.
d) temperatura, velocidade e volume.
e) massa, temperatura e força.
2

25. 02. (PUC-MG) Para o diagrama vetorial abaixo, a única
igualdade correta é:
2

26. 03. Dados vetores e , de mesma direção, mesmo sentido
e de módulos, respectivamente, iguais a 2 e 3, calcule o
módulo do vetor soma.
2

27. 04. Dados vetores e , perpendiculares entre si, e de
módulos, respectivamente, iguais a 6 e 8, calcule o
módulo do vetor soma.
2

28. Dados vetores
graficamente o
e , perpendiculares entre si, represente
vetor soma e calcule seu módulo.
Considere a medida de cada quadradinho igual a uma
unidade (1 u).
2