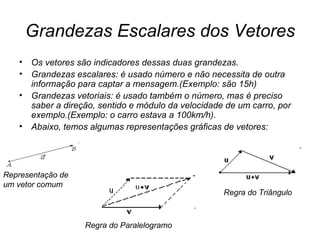
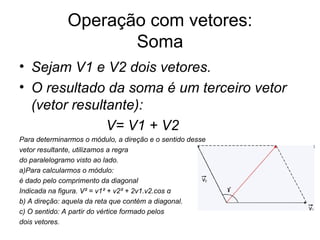
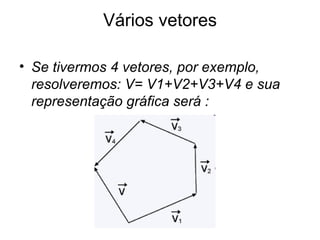
O documento discute vetores, incluindo suas propriedades, representações gráficas e operações. Grandezas vetoriais como velocidade requerem informações de direção e sentido, diferente de escalares como tempo. Vetores podem ser somados ou subtraídos usando regras do paralelogramo ou triângulo, determinando módulo, direção e sentido do resultado. Exemplos ilustram cálculos com duas forças.

1. Vetores Mariana Mendes, 2ºC Ana Carolina, 2º C

2. Grandezas Escalares dos Vetores Os vetores são indicadores dessas duas grandezas. Grandezas escalares: é usado número e não necessita de outra informação para captar a mensagem.(Exemplo: são 15h) Grandezas vetoriais: é usado também o número, mas é preciso saber a direção, sentido e módulo da velocidade de um carro, por exemplo.(Exemplo: o carro estava a 100km/h). Abaixo, temos algumas representações gráficas de vetores: Regra do Paralelogramo Regra do Triângulo Representação de um vetor comum

3. Operação com vetores: Soma Sejam V1 e V2 dois vetores. O resultado da soma é um terceiro vetor (vetor resultante): V= V1 + V2 Para determinarmos o módulo, a direção e o sentido desse vetor resultante, utilizamos a regra do paralelogramo visto ao lado. a)Para calcularmos o módulo: é dado pelo comprimento da diagonal Indicada na figura. V² = v1² + v2² + 2v1.v2.cos α b) A direção: aquela da reta que contém a diagonal. c) O sentido: A partir do vértice formado pelos dois vetores.

4. Operação com vetores: Subtração Na subtração também haverá um terceiro vetor que será o resultado da subtração de V1 por V2. O vetor tem módulo e direção iguais ao do vetor V2, mas tem o sentido oposto.

5. Vários vetores Se tivermos 4 vetores, por exemplo, resolveremos: V= V1+V2+V3+V4 e sua representação gráfica será :

6. Exercícios Dado os vetores a e b, determine a distância entre ambos. (Dados: cos 60º = 0,5 ) RESOLUÇÃO: S² = a² + b² + 2 · a · b · cos 60º S² = 3² + 4² + 2 · 3 · 4 · 0,5 S² = 9 + 16 + 12 S √37 = 6,1 cm 2) Duas forças F1 e F2, têm módulos iguais a 10N cada uma.Calcule o módulo da resultante quando o ângulo Ө entre F1 e F2 for igual a: 0º c) F² = F1² + F2² 180º F² = (10N)² + (10N)² 90º F² = 200 N RESOLUÇÃO: F = √200 N F= F1+F2 F = 10 √2 N F= 10N+10N F= 20N b) F= F1 – F2 F= 10N -10N = 0N