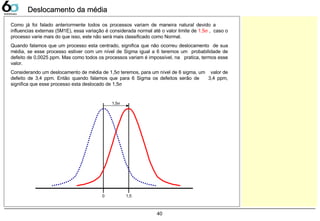
- O documento apresenta os conceitos e métodos do Treinamento 6σ na LG Electronics, incluindo: 1) A importância da inovação e do gerenciamento 6σ para a empresa; 2) Os objetivos, princípios e métodos do 6σ; 3) A estrutura do departamento de gerenciamento de inovação da LG responsável pelo 6σ.

![ Índice
3
LG Electronics Green Belt [Mfg]
Introdução 05
Estatística Básica 19
SIPOC 21
Coleta de Dados (amostragem) 22
Tipos de Dados (discretos e contínuos) 23
- Dados Contínuos
Média 25
Mediana 27
Moda 28
Desvio Padrão 29
Variância 30
Amplitude 31
- Dados Discretos
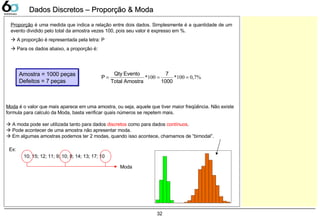
Proporção e Moda 32
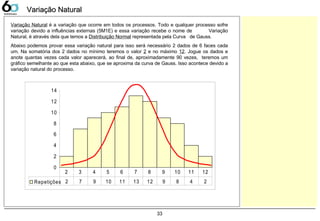
Variação Natural 33
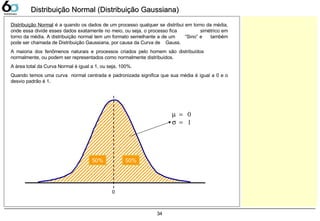
Distribuição Normal 34
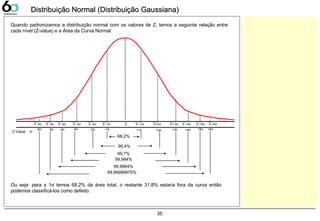
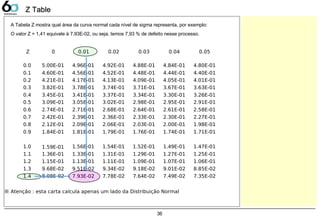
Z-Table 36
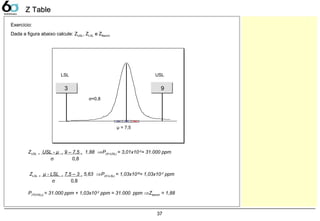
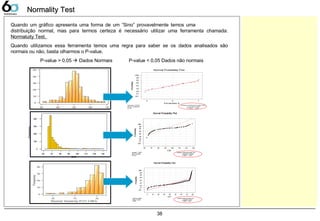
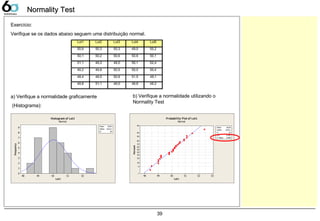
Normality Test 38
Deslocamento da Média 40
Definição 41
Resumo
Seleção do Projeto 43
Extração do Y 44
Registro do Projeto 45
Ferramentas 46
Brainstorming 47
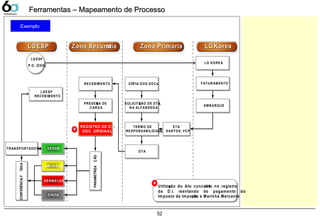
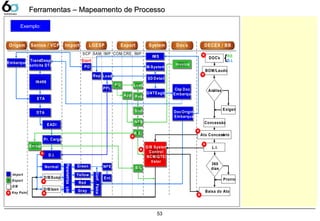
Mapeamento do Processo 49
FMEA 54
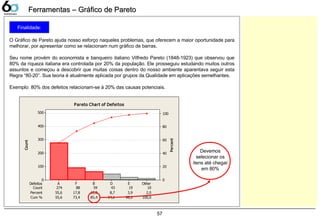
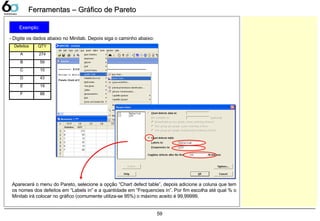
Gráfico de Pareto 57
QFD 61
Meta & Cronograma 64
Estimativa de Ganho e Registro 65
Medição 66
Resumo
Verificar as propriedades do Y do Projeto 68
Verificar nível atual (Z-value) 69
Entendendo o Z-value 70
Coleta de Dados (Rational Subgrouping) 71
Tipos de Gage 72
Gage R&R 73
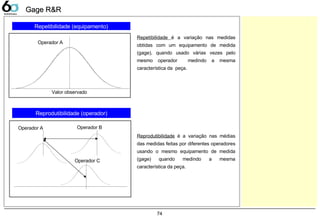
Repetibilidade / Reprodutibilidade 74
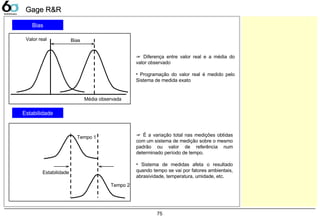
Bias / Estbilidade 75
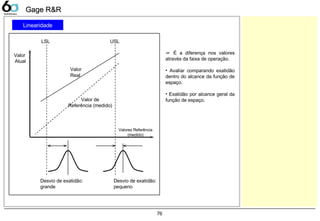
Linearidade 76
Regra de Thumb 78
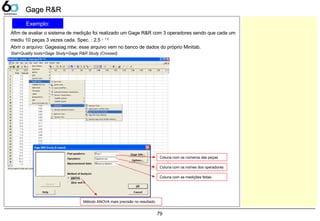
Exemplo 79
Gráficos 83
Gage Attribute 84
Exemplo MInitab 85](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-3-320.jpg)
![ Índice
4 LG Electronics Green Belt [Mfg]
Cálculos 87
Exemplo feito manualmente 88
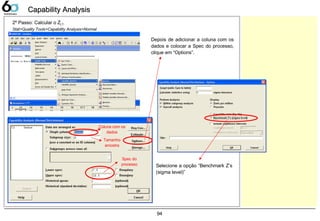
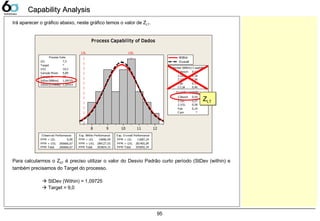
Calculando o Z-value 90
Dados Contínuos
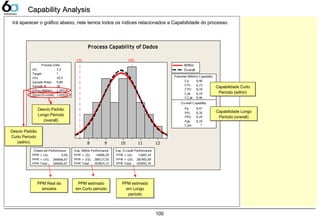
Capability Analysis 91
Fórmulas CP/PP/Cpk/Ppk 92
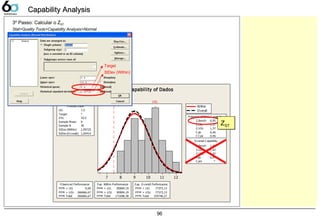
Calculo ZST/ZLT/ZShift no Minitab 93
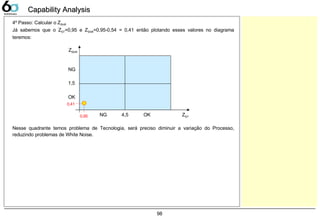
Diagrama de 4 Blocos 97
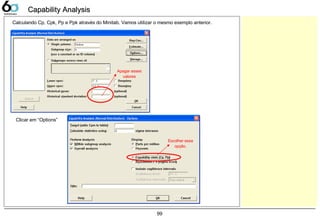
Calculo Cp/Cpk/Pp/Ppk no Minitab 99
Dados Discretos
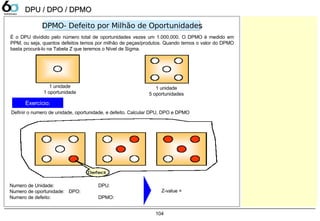
DPU/DPO/DPMO 102
Exemplo 103
Análise 107
Resumo
Selecionar o fator Vital 109
Examinar a causa raiz 110
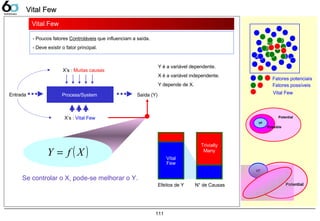
Vital Few 111
Introdução 112
Introdução ao Minitab 113
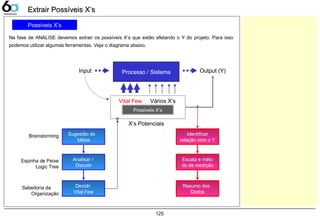
Extrair Possíveis X’s 125
Espinha de Peixe (Fish Bone) 126
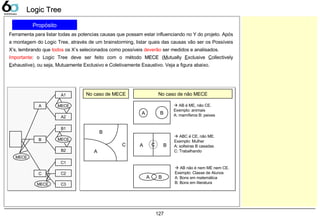
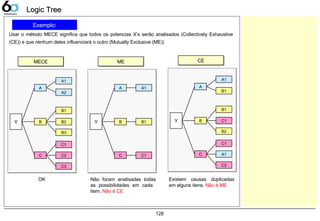
Logic Tree (MECE) 127
Análise dos Possíveis X’s 129
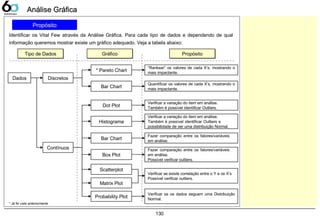
Análise Gráfica 130
- Dados Discretos
Bar Chart 131
- Dados Contínuos
Dot Plot 133
Histograma 136
Bar Chart 138
Box Plot 139
Descriptive Statistics 141
Graphical Summary 143
Scatter Plot 144
Correlation 145
Matrix Plot 146
Probability Plot 148
Testes de Hipótese 150
Definição 151
Erros (α e β) 152
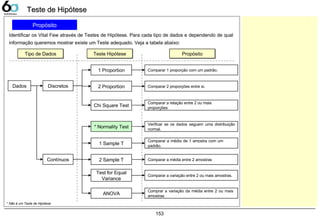
Tipos de Teste 153
- Dados Discretos
1 Proportion 154
2 Proportion 155
Chi-Square Test 156](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-4-320.jpg)
![ Índice
5 LG Electronics Green Belt [Mfg]
Dados Contínuos
Normality Test 157
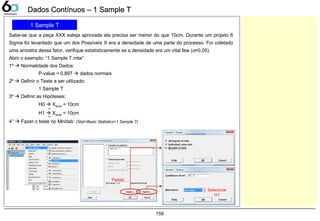
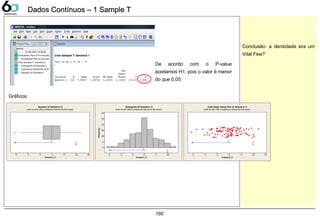
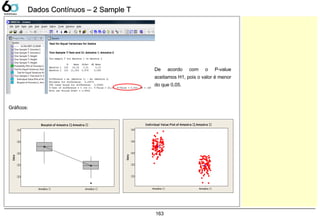
1 Sample T 159
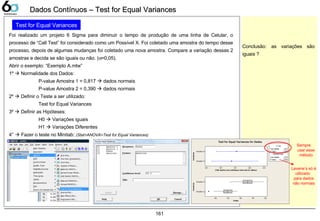
Test for Equal Variances 161
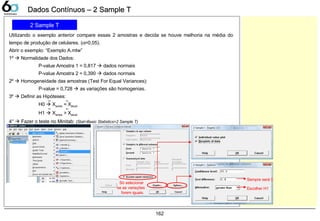
2 Sample T 162
ANOVA 164
Correlação e Analise de Regressão 167
Correlação 167
Exemplo 168
Equação de Regressão 169
Gráfico 171
Melhoria 172
Resumo
Estabelecer o plano otimizado 174
Executar e inspecionar 175
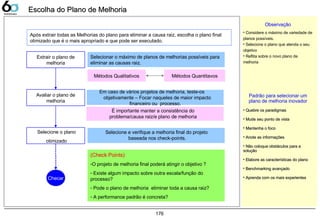
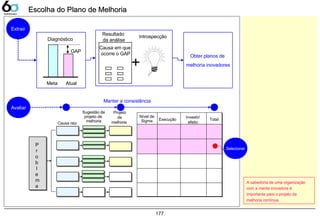
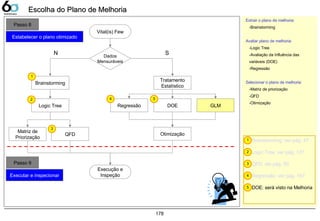
Escolha do Plano de Melhoria 176
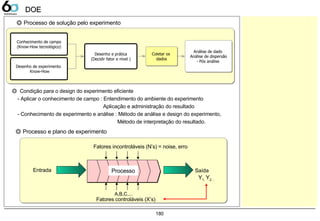
DOE (Design of Experiment) 179
3 Princípios de um Experimento 181
Exemplo 182
Identificando o Main Effect 187
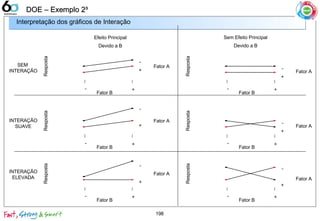
Identificando as Interações 190
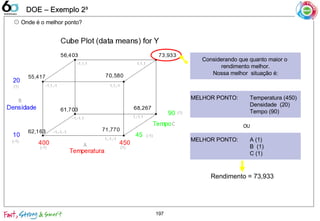
Identificando o melhor Ponto (Cube Plot) 191
DOE com 3 Fatores 192
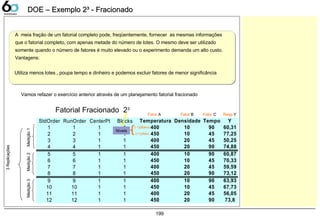
DOE Fracionado 199
Execução e inspeção das Melhorias 201
Controle 203
Resumo
Padronizar 204
Monitorar 204
Compartilhar o Resultado 204
Padronizar 205
Sistema a prova de falhas Poka Yoke 206
Sistema de Monitoramento 207
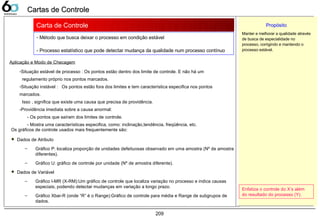
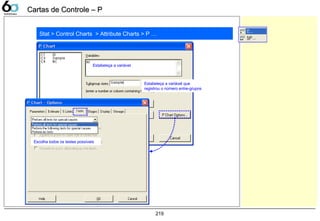
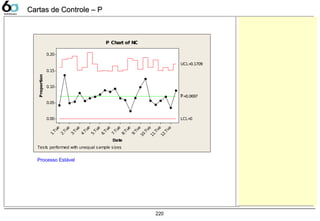
Cartas de Controle 209
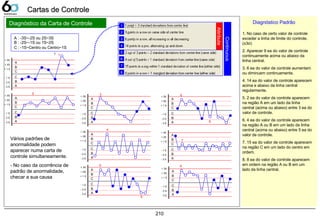
Regras da Carta 210
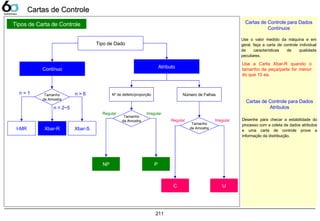
Tipos de cartas 211
- Dados Contínuos
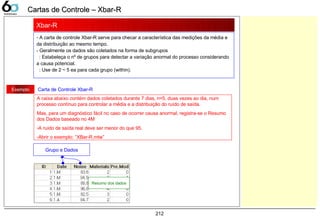
XBar-R 212
- Dados Discretos
NP 215
P 218
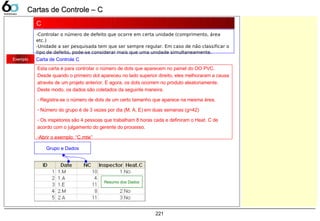
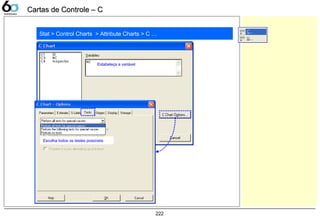
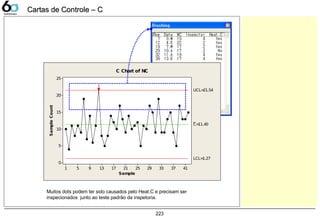
C 221
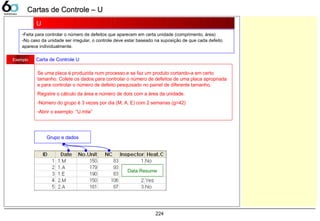
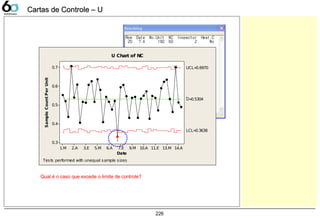
U 224
Revisão Geral 227](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-5-320.jpg)
![INTRODUÇÃO
6
1
- Entender o conceito de inovação e a importância da atividade da Inovação.
- Entender o propósito do gerenciamento 6σ na LGE.
- Entender a filosofia e princípio do 6σ bem como o método de apresentação.
Objetivos
LG Electronics Green Belt [Mfg]](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-6-320.jpg)

![1987 Galvin CEO
Mikel J Harry, Ph.D
1997
1995
3M
2001
SSA
1994
AT&T
Jack Welch
1996
História doHistória do 66σσ
8
LG Electronics Green Belt [Mfg]](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-8-320.jpg)



![16
Estrutura Departamento de Inovação (Six Sigma)Estrutura Departamento de Inovação (Six Sigma)
S. Y. HanS. Y. Han
DiretorDiretor
GerenteGerente
RogérioRogério
Six SigmaSix Sigma
César PintorCésar Pintor
Pedro GamaPedro Gama
Departamento de Gerenciamento de Inovação [DGI – Six Sigma]
Estrutura do Departamento de Gerenciamento de Inovação (Six Sigma) segue abaixo:
jimmy.han@lge.com
rogerio.martins@lge.com
12-2125-5518
cesar.alcantara@lge.com
12-2125-5570
pedro.gama@lge.com
12-2125-5684
* Atualizado em jan/2011](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-16-320.jpg)

![ESTATÍSTICA BÁSICA
19
2
- Entender sobre Estatística Básica.
- Conhecer os termos utilizadosObjetivos
LG Electronics Green Belt [Mfg]](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-19-320.jpg)


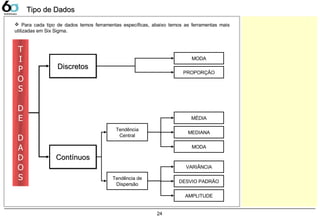



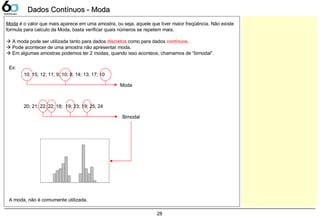
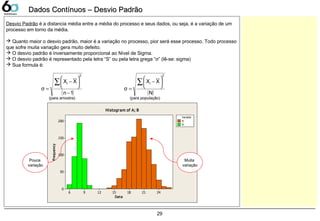

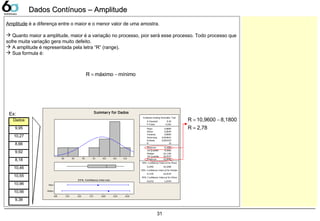
![DEFINIÇÃO
41
3
Passo 1. Seleção de projeto
Passo 2. Extrair o Y do Projeto
Passo 3. Registro do projeto
- Entender os itens que influenciam o ponto de vista do cliente e negócio e selecionar o tema do
projeto.
- Extrair a possibilidade de melhoria através do processo do projeto selecionado.
- Definir o item a melhorar.
Meta
Ferramenta
Passos
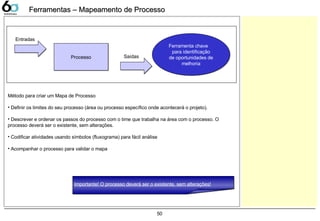
- SIPOC, Mapeamento do processo
- Logic Tree, Diagrama de espinha de peixe
- QFD, FMEA, Análise de Pareto
LG Electronics Green Belt [Mfg]](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-41-320.jpg)











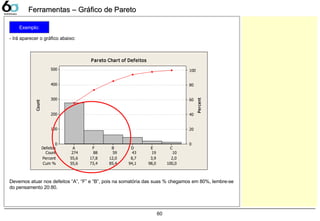




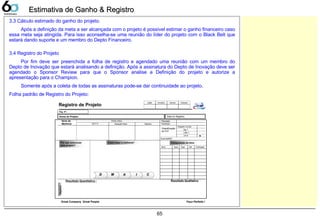
![66
4
Medição
- Entender a importância da medição.
- Entender o método correto para coletar os dados.
- Verificar a condição atual do processo.
- Decidir a direção e a extensão da melhoria.
Metas
Ferramentas
Passos
PASSO 4 : Verificar as características do Y do Projeto
PASSO 5 : Verificar a condição atual
- Análise do sistema de medição : Gage R&R
- Análise da capacidade do processo : Nível de sigma, DPU, DPO, DPMO
- Diagrama de 4 Blocos
LG Electronics Green Belt [Mfg]](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-66-320.jpg)



![70
Entendendo o Z-ValueEntendendo o Z-Value
Propósito
A escala σ (Z-value) é uma métrica para medir o nível de qualidade de um
produto/processo/serviço. Da mesma maneira que utilizamos metros [m] para distância e
graus Celsius [ºC] para temperatura, utilizamos o Z-Value como uma linguagem comum.
Desta forma, diferentes departamentos podem verificar o nível da qualidade um do outro.
Exemplo:
A velocidade média de um carro de fórmula 1 é de aproximadamente 300km/h, com um
desvio padrão de 10km/h.
300
+1σ
310 320 330280 290270
µ µ+1σ µ+2σ µ+3σµ-2σ µ-1σµ-3σ
300 310 320 330280 290270
EIXO de X
1 2 3-2 -1-3
0
EIXO de Z
µ = 300
σ = 10
µ = 300
σ = 10](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-70-320.jpg)

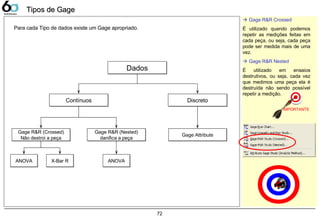
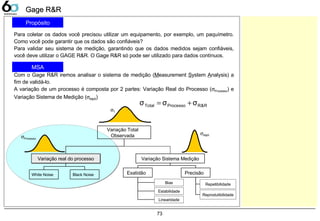


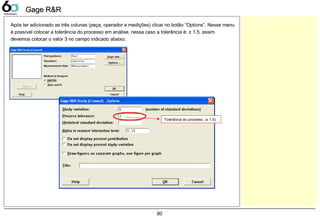
![82
Nº categorias
distintas
Significado
1 Se a variação do Sistema de Medição for semelhante a variação
real do processo não é possível avaliar este processo, com isso o
número de categorias cai.
Sistema inapropriado.
2~4 Não é possível detectar a variação do processo mesmo utilizando
uma carta de controle, pois a sensibilidade do equipamento ainda
não consegue distinguir as várias categorias.
Sistema inapropriado.
≥ 5 Nessa faixa já é possível verificar e gerenciar as variações
existentes no processo, com isso o Sistema de Medição se torna
confiável.
Sistema apropriado
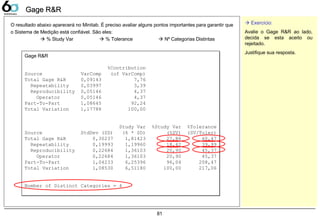
% Study Var Avalia se o Sistema de Medição é capaz de detectar a variação do processo ou
não. Isto significa que esse sistema é apropriado.
% Tolerance Mostra a exatidão do Sistema de Medição de acordo com a tolerância do
processo, avalia se é possível detectar se a peça esta boa ou ruim.
Nº Categorias
Distintas
Avalia se o Sistema de Medição consegue distinguir as variações do processo.
Descreve quantos grupos diferentes o sistema consegue distinguir, quanto maior
melhor será o resultado.
Significado:
Gage R&RGage R&R
Tolerância do Equipamento.
Quando for necessário utilizar
um equipamento para realizar
um Gage R&R sua resolução
deve ser de 1/10 da tolerância
do processo.
Ex.: Se a Spec for 2±0,5
[cm]
significa que a tolerância é de
±0,5 [cm], nesse caso o
equipamento tem que ter a
capacidade de medir 1/10
desse valor, ou seja:
O equipamento tem que
conseguir medir nessa escala.
[cm]0,0050,05*
10
1
Equip.Tol. ==](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-82-320.jpg)
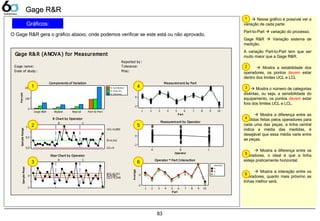
![84
Gage AttributeGage Attribute
Propósito
O que são dados atributos?
São os dados do tipo: OK / NG ou Verde / Amarelo. Normalmente são utilizados quando
estamos avaliando um operador, se este sabe ou não inspecionar algum ponto do
processo/produto/serviço.
Neste caso devemos trabalhar da seguinte forma:
Nº Operadores Mínimo peças avaliadas Mínimo repetições
1 24 5
2 18 4
3 12 3
Estatística Apropriado Aceito condicional Inapropriado
Eficiência
[PE]
90~100 % 80~90 % Abaixo 80 %
Alarme Falso [PFA] 0~5 % 5~10 % Acima 10 %
Perda
[Pmiss]
0~2 % 2~5 % Acima 5 %
Regra:
Importante: cuidado com as medidas de fronteira (ex.: PFA = 5%, pode ser simultaneamente
classificado como “Apropriado” e “Aceito Condicionalmente”)](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-84-320.jpg)
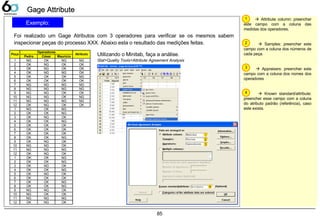
![87
Gage AttributeGage Attribute
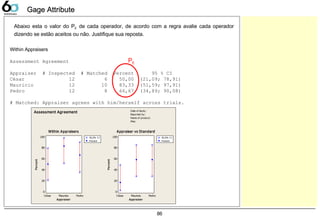
Cálculos:
As probabilidades (PE, PFA e Pmiss) podem ser calculadas sem o Minitab através das seguintes
fórmulas:
[%]100*
ções)Peças(mediTotal
AcertosQtde
=
PE é a taxa de acerto de cada operador. O
calculo é realizado através da divisão do total
de medições corretas pelo total de peças
inspecionadas.
[%]100*
medidasrepeticoesTotal*padrãoboaspeças
FalsoAlarmeQtde
PFA =
PFA é a taxa de alarme falso. Alarme falso é o
erro que o operador comete quando julga uma
peça “BOA” como “RUIM”. Esse tipo de erro
não é tão grave quanto o PMiss, mas diminui a
eficiência da linha de produção.
[%]100*
repetiçõesTotal*padrãoruinsPeças
ErroQtde
P Perda
Miss =
PMiss é o erro que o operador comete quando
julga uma peça “RUIM” como “BOA”. Esse tipo
de erro é bem grave, pois o operador deixa
entrar no processo peças com defeito. Sendo
esse tipo de erro muito alto, o defeito chegará
no cliente.](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-87-320.jpg)

![92
LSL USL
Cp = 2.0
Cp = 1.33
Cp = 0.6
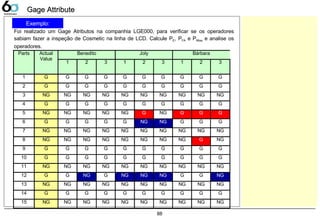
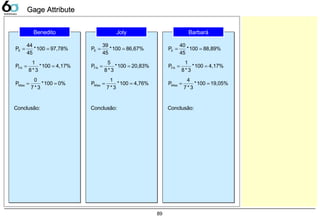
Capability AnalysisCapability Analysis
Cp, Cpk, Pp, Ppk
Analisando graficamente temos:
Podemos verificar que
quanto maior a variação
menor será o Cp/Pp.
Podemos verificar que
quanto maior a variação
menor será o Cp/Pp.
LSL USLCpk = 1,5
Cpk = 1,00
Cpk = 0,45
Podemos verificar que
quanto maior o
deslocamento menor será
o Cpk/Ppk.
Podemos verificar que
quanto maior o
deslocamento menor será
o Cpk/Ppk.
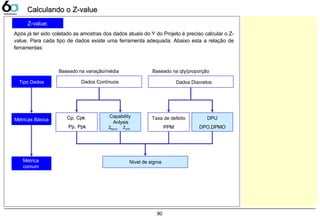
Fórmulas:
periodo)towithin(cur6.σ
LSLUSL
Cp
−
=
periodo)ngooverall(lo6.σ
LSLUSL
Pp
−
=
T
T
k
k
k
k)Pp.(1Ppk
k)Cp.(1Cpk
−=
−=
Fórmulas:
Cp/Pp
Cpk/Ppk
2
LSL-USL
TX
k
−
=
within3.σ
XUSL
CPU
−
=
ou
within3.σ
LSLX
CPL
−
=
CPL]min[CPU;Cpk =
overall3.σ
XUSL
PPU
−
=
overall3.σ
LSLX
PPL
−
=
PPL]min[PPU;Ppk =](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-92-320.jpg)







![107
5
Análise
- Selecionar o fator principal examinando o X possível.
- Examinar rigorosamente a causa do fator principal ou do defeito.
- Análise Gráfica
- Interferência estatística : Intervalo de Estimativa & Test de Hipótese
- Análise de Regressão
Objetivos
Ferramentas
Passos
Passo 6 : Selecionar o fator principal (Vital Few)
Passo 7 : Examinar a principal causa
LG Electronics Green Belt [Mfg]](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-107-320.jpg)



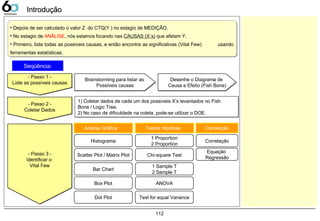
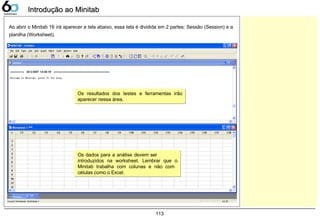
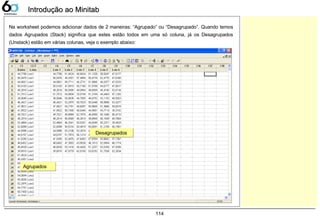
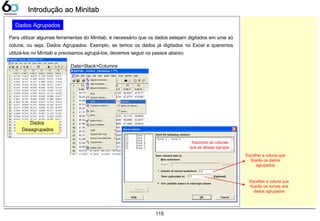
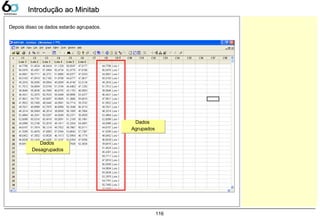
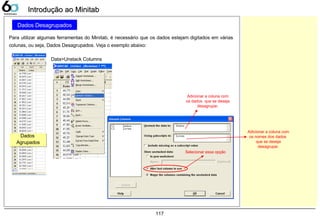
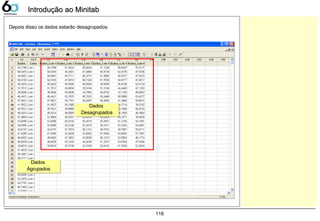

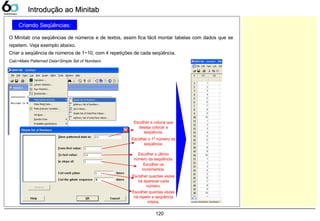


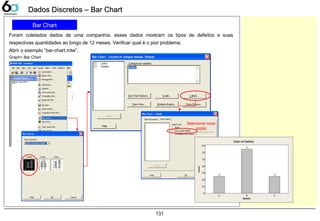
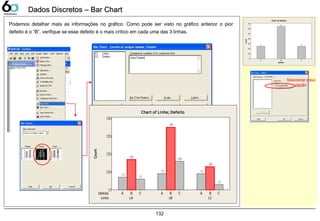
![133
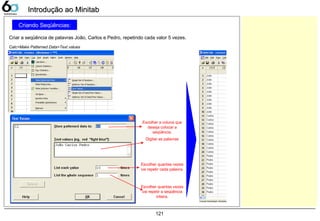
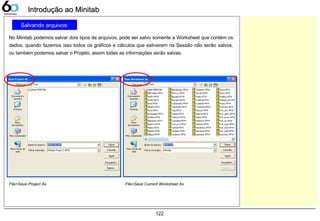
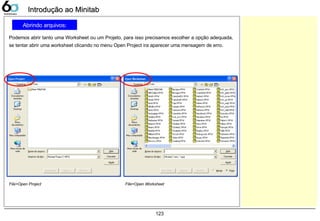
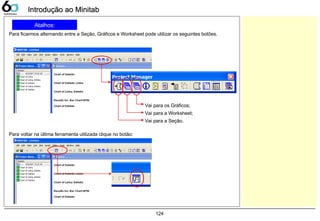
Dados Contínuos – Dot PlotDados Contínuos – Dot Plot
Dot Plot
A companhia LGE000 produz telefones celulares, atualmente 3 fornecedores fabricam baterias para sua
produção. Verifique as variações entre estes fornecedores, sabendo que a característica medida foi a
tensão elétrica fornecida pela bateria, sua faixa pode variar de 3,0 ~ 4,2 [V].
Abrir o exemplo: “Dot-plot.mtw”
Graph> Dot Plot
Tensão [V]
3,923,783,643,503,363,223,08
Dotplot of Tensão [V]](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-133-320.jpg)
![134
Dados Contínuos – Dot PlotDados Contínuos – Dot Plot
Separando os dados por fornecedores.
Tensão [V]
Fornecedor
7,777,777,777,777,777,777,77
Fornecedor A
Fornecedor B
Fornecedor C
Dotplot of Tensão [V] vs Fornecedor](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-134-320.jpg)
![135
Dados Contínuos – Dot PlotDados Contínuos – Dot Plot
Outliers são pontos distantes do resto da amostra, normalmente são problemas que aconteceram durante
a coleta de dados. Toda vez que for encontrado outliers é essencial que este seja removido, mas para
isso é preciso saber porque ele esta na amostra.
A presença de outliers pode fazer com que uma amostra seja transformada em dados não normais, dessa
forma é impossível realizar a análise.
Identificando outliers no Minitab:
Outliers
Clicar botão direto do
mouse sobre o gráfico
Outliers
Outliers:
3,44185 [V]
3,44973 [V]](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-135-320.jpg)
![136
Dados Contínuos – HistogramaDados Contínuos – Histograma
Histograma
Vamos utilizar o mesmo exemplo do gráfico anterior.
Abrir o exemplo: “Dot-plot.mtw”
Graph> Histogram
Tensão [V]
Frequency
3,903,753,603,453,303,153,00
50
40
30
20
10
0
Histogram of Tensão [V]](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-136-320.jpg)
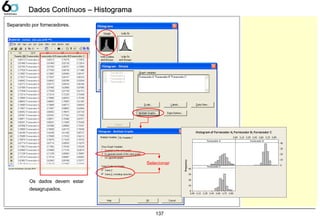
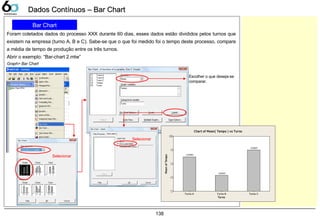
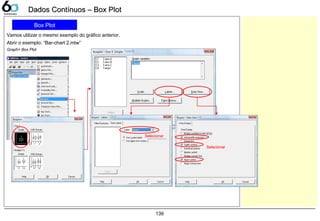
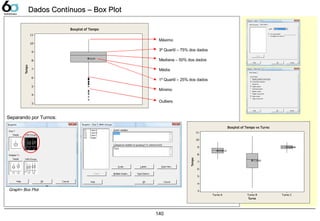

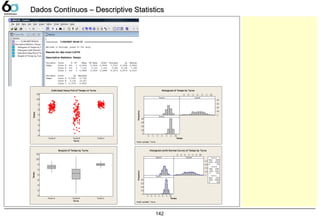
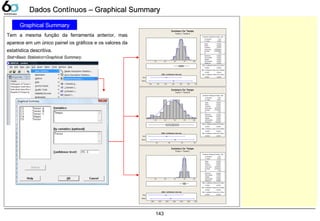
![144
Dados Contínuos – ScatterplotDados Contínuos – Scatterplot
Scatterplot
Sabe-se que conforme aumentamos a temperatura no forno [°C] o comprimento do produto varia, verifique
se existe uma correlação entre o aumento da temperatura e o comprimento da peça [cm].
Abrir o exemplo: “Scatterplot.mtw”
Graph> Scatterplot
NÃO inverter
X com Y
Temp [°C]
Comp.[cm]
120115110105100
22
21
20
19
18
17
16
15
14
13
Scatterplot of Comp. [cm] vs Temp [°C] Existe correlação?](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-144-320.jpg)
![146
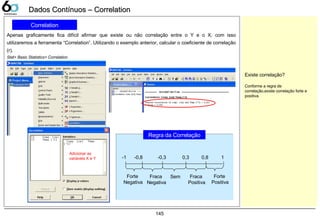
Dados Contínuos – Matrix PlotDados Contínuos – Matrix Plot
Matrix Plot
Utilizamos o matrix plot quando temos mais do que um X para verificar a correlação com o Y.
No exemplo anterior tínhamos o Y sendo a comprimento da peça e o X sendo a temperatura, agora, além
da temperatura, descobrimos que o tempo em que a peça fica no forno também esta influenciando a
produção.
Abrir o exemplo: “Matrix Plot.mtw”
Graph> Matrix Plot
Temp [°C]
Comp.[cm]
120115110105100
22
21
20
19
18
17
16
15
14
13
Tempo [s]
161514
Matrix Plot of Comp. [cm] vs Temp [°C]; Tempo [s]](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-146-320.jpg)
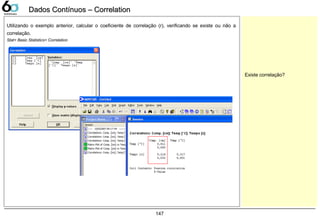
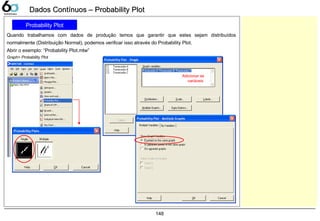
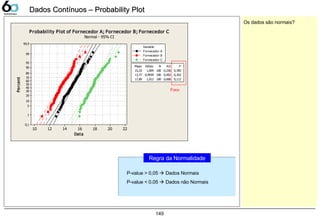


![Teste de HipóteseTeste de Hipótese
α = erro tipo I
H0 é verdadeiro, seleciono H1
β = erro tipo II
H1 é verdadeiro, seleciono H0
Erro α é quando rejeitamos a hipótese
verdadeira. (risco do fornecedor)
Erro β é quando aceitamos a hipótese
falsa. (risco do cliente)
O “P-value” é a probabilidade de se obter uma estatística para o teste onde poderemos aceitar ou rejeitar a hipótese nula (H0).
Ele é o menor nível no qual H0 pode ser rejeitado.
Aceitar H0Aceitar H0
α = 0,05
α*100 = 5% Nível de Significância
α = 0,05
α*100 = 5% Nível de Significância
C.L. = 1- α
C.L. = 0,95
C.L.*100 = 95% Nível de Confiança
C.L. = 1- α
C.L. = 0,95
C.L.*100 = 95% Nível de Confiança
Regra de P-value:
P-value > α Aceita H0
P-value < α Rejeita H0
Regra de P-value:
P-value > α Aceita H0
P-value < α Rejeita H0
2,5%2,5%
95%95%
2,5%2,5%
O valor de “α” no gráfico ao lado é de 5%, então se P-value for menor que
ele, nós rejeitaremos a Hipótese nula (H0), por conseqüência iremos
aceitar a hipótese alternativa (H1).
Será dessa forma que iremos utilizar os testes de hipótese, sempre
analisando o “P-value” e comparando-o com o nível significante (α).
*Obs.: o valor de α é o quanto estaremos aceitando o erro de rejeitarmos o H0,
quando na verdade deveríamos aceita-lo. O C.L. nos mostra a
confiabilidade do teste, sendo que quanto maior o “α” pior será essa
confiabilidade.
α/2 α/2C.L.
LG Electronics Green Belt [Mfg]
152
Erro α e β
P-value:](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-152-320.jpg)

![156
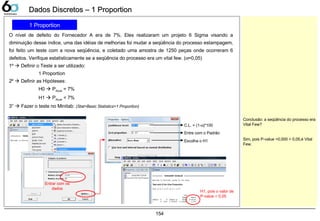
Dados Discretos – Chi-Square Test [Dados Discretos – Chi-Square Test [χχ²]²]
Chi-Square Test
Suponha que seja realizada uma pesquisa para determinar se existe relação entre o local de residência
e a preferência por monitores. Uma amostra aleatória de 200 proprietários de monitores da cidade
grande, 150 do subúrbio e 150 na zona rural foi selecionada. Verifique estatisticamente se o local de
residência era um vital few. (α=0,05)
Abrir o exemplo: “Chi-square Test.mtw”
1º Definir o Teste a ser utilizado:
Chi-Square Test
2º Definir as Hipóteses:
H0 Não existe relação entre Vendas e o Local de Residência
H1 Existe relação entre Vendas e o Local de Residência
3° Fazer o teste no Minitab: (Stat>Tables>Chi-Square Test)
Entrar com os
dados
H1, pois o valor de
P-value < 0,05
Conclusão: o local de residência era
Vital Few?](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-156-320.jpg)
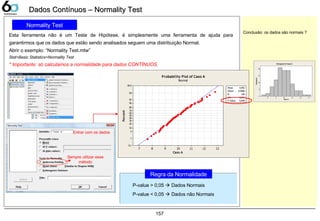
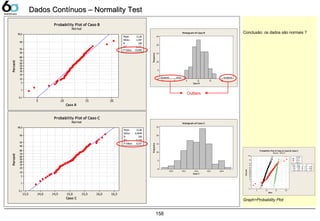
![Dados Contínuos – ANOVADados Contínuos – ANOVA
Propósito
Média Geral
A
B
C
• Analysis of Variance, esse teste de hipótese é indicado
quando deseja-se verificar a variação da média entre as
amostras coletadas.
• Utilizamos a ANOVA quando temos 3 ou mais
amostras
• Pré-requisitos da ANOVA:
- Aleatoriedade dos dados;
- Normalidade dos dados;
- Homogeneidade das variações.
Grupo Dados
1 25
1 26
1 27
1 24
1 29
2 35
2 39
2 38
2 37
2 34
3 42
3 45
3 49
3 44
3 48
Se há 3 grupos, nós podemos calcular 4 médias diferentes.
● Média Total : 36.1
● Média do Grupo 1 : 26.2
● Média do Grupo 2 : 36.6
● Média do Grupo 3 : 45.6
Se a taxa de variação entre os subgrupos e a variação dentro dos
subgrupo é grande, nós podemos dizer que há uma grande
diferença entre os subgrupos
F < 1, variação pequena entre os grupos
Entendendo ANOVAEntendendo ANOVA
1
SubgruposdentroVariação
SubgruposentreVariação
F >=
164
LG Electronics Green Belt [Mfg]](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-164-320.jpg)
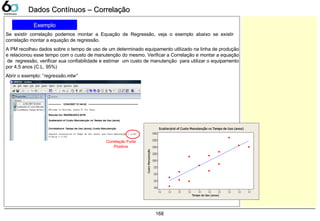
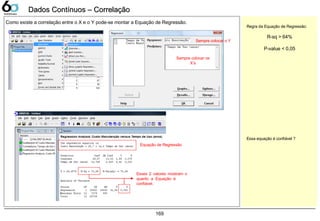
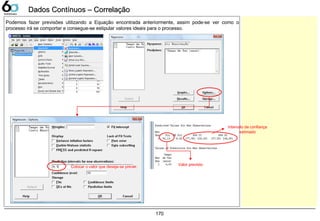
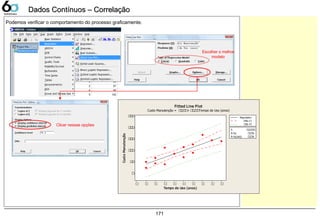
![Melhoria
- Encontrar e selecionar o método de melhoria para resolver a causa raiz do fator vital
- Verificar o efeito da melhoria aplicando-a nos negócios
Metas
Ferramentas
Etapas
Fase 8. Selecionar o melhor projeto
Fase 9. Executar e Verificar o mesmo
- Compreender os vários métodos de projeto e seus métodos de análise.
- Compreender o efeito e aplicá-los na prática.
- Compreender os vários padrões qualitativos que se transformam em um padrão de pensamento sistemático
- Brainstorming, Logic Tree, Matriz de Priorização, QFD (revisão)
- Regressão (revisão) e Design de Experimento (DOE)
172
LG Electronics Green Belt [Mfg]
6](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-172-320.jpg)





![187
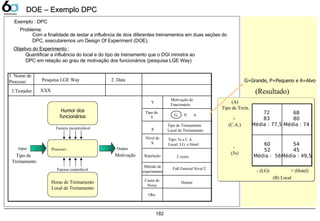
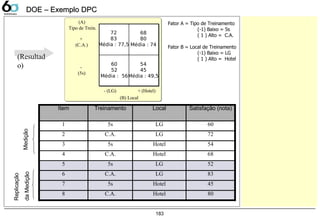
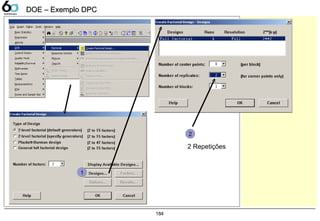
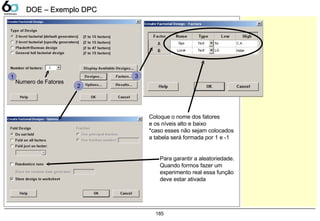
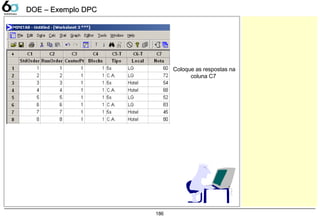
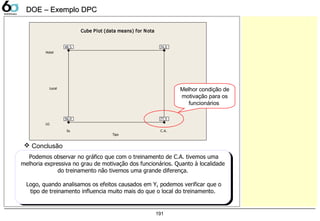
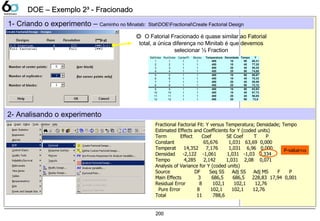
DOE – Exemplo DPCDOE – Exemplo DPC
Entre com a coluna que
contem o resultado
1
2
3
LG Electronics Green Belt [Mfg]
187](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-187-320.jpg)
![195
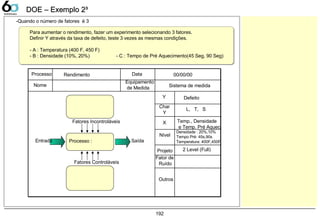
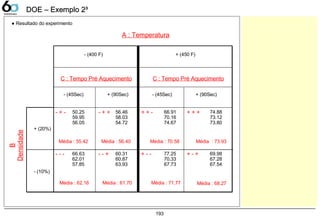
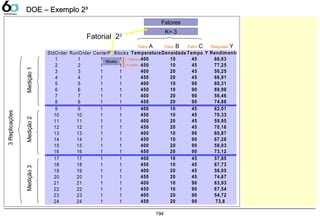
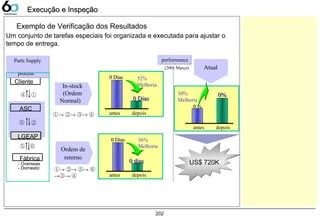
DOE – Exemplo 2DOE – Exemplo 2³³
Fractional Factorial Fit: y versus Temp, Density, Pre
Estimated Effects and Coefficients for y (coded units)
Term Effect Coef SE Coef T P
Constant 65.0296 0.6924 93.91 0.000
Temp 12.2158 6.1079 0.6924 8.82 0.000
Density -1.8925 -0.9462 0.6924 -1.37 0.191
Pre 0.0942 0.0471 0.6924 0.07 0.947
Temp*Density 4.1308 2.0654 0.6924 2.98 0.009
Temp*Pre -0.1692 -0.0846 0.6924 -0.12 0.904
Density*Pre 2.0758 1.0379 0.6924 1.50 0.153
Temp*Density*Pre 1.3525 0.6762 0.6924 0.98 0.343
Analysis of Variance for y (coded units)
Source DF Seq SS Adj SS Adj MS F P
Main Effects 3 916.90 916.90 305.63 26.56 0.000
2-Way Interactions 3 128.41 128.41 42.80 3.72 0.033
3-Way Interactions 1 10.98 10.98 10.98 0.95 0.343
Residual Error 16 184.11 184.11 11.51
Pure Error 16 184.11 184.11 11.51
Total 23 1240.40
Fractional Factorial Fit: y versus Temp, Density, Pre
Estimated Effects and Coefficients for y (coded units)
Term Effect Coef SE Coef T P
Constant 65.0296 0.6924 93.91 0.000
Temp 12.2158 6.1079 0.6924 8.82 0.000
Density -1.8925 -0.9462 0.6924 -1.37 0.191
Pre 0.0942 0.0471 0.6924 0.07 0.947
Temp*Density 4.1308 2.0654 0.6924 2.98 0.009
Temp*Pre -0.1692 -0.0846 0.6924 -0.12 0.904
Density*Pre 2.0758 1.0379 0.6924 1.50 0.153
Temp*Density*Pre 1.3525 0.6762 0.6924 0.98 0.343
Analysis of Variance for y (coded units)
Source DF Seq SS Adj SS Adj MS F P
Main Effects 3 916.90 916.90 305.63 26.56 0.000
2-Way Interactions 3 128.41 128.41 42.80 3.72 0.033
3-Way Interactions 1 10.98 10.98 10.98 0.95 0.343
Residual Error 16 184.11 184.11 11.51
Pure Error 16 184.11 184.11 11.51
Total 23 1240.40
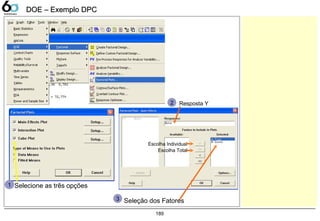
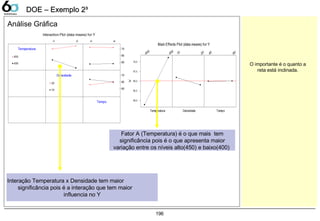
Numericamente: Podemos confirmar o que o gráfico nos
apresenta: que a temperatura e a Interação
Temperatura/densidade são significativos em sua
influencia na resposta Y (Rendimento),
pois p-value < α. (Para o caso α=0,1)
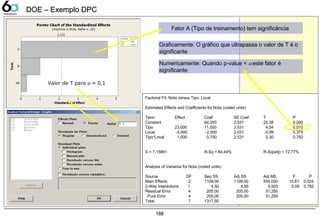
- Para determinarmos os efeitos principais ou quais tem significância podemos utilizar tanto a análise
gráfica como a numérica
0 1 2 3 4 5 6 7 8 9
C
AC
ABC
B
BC
AB
A
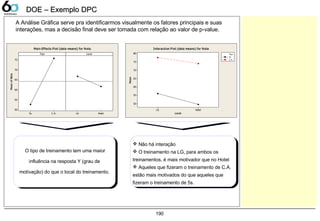
Pareto Chart of the Standardized Effects
(response is Y Rendim, Alpha = ,10)
A: Temperat
B: Densidad
C: Tempo
Fator A (Temperatura) tem
significância
Interação Temperatura x Densidade
tem significância
Pareto dos efeitos e interações Análise Numérica
LG Electronics Green Belt [Mfg]
195](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-195-320.jpg)









![232
LG Electronics Green Belt [Mfg]
General Administration
Innovation
Human Resource
Suporte Black BeltSuporte Black Belt](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-232-320.jpg)
![233
LG Electronics Green Belt [Mfg]
Suporte Black BeltSuporte Black Belt
Notebook
Washing Machine](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-233-320.jpg)
![234
LG Electronics Green Belt [Mfg]
Suporte Black BeltSuporte Black Belt
Purchase / Material (MNT)
Production Cellular
GERENTE](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-234-320.jpg)
![235
LG Electronics Green Belt [Mfg]
Suporte Black BeltSuporte Black Belt
Engineering (MNT/ CELL/ WM)](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-235-320.jpg)
![236
LG Electronics Green Belt [Mfg]
Suporte Black BeltSuporte Black Belt
Production MNT](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-236-320.jpg)
![237
LG Electronics Green Belt [Mfg]
Suporte Black BeltSuporte Black Belt
Quality (MNT/ CELL)
Total = 31 Black Belt](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-237-320.jpg)
![238
LIVRO DE 6 SIGMA PARA GREEN BELTS - MFG
• Data emissão: 27/01/2011 [rev. 01]
• Departamento de Inovação [DGI]
• Desenvolvido por: César Pintor [BB]
Diego Gutierres [BB]
Mauricio Fulgêncio [BB]
LG Electronics Green Belt [Mfg]](https://image.slidesharecdn.com/lg-sixsigma-130917050849-phpapp01/85/Treinamento-Six-Sigma-LG-Electronics-238-320.jpg)