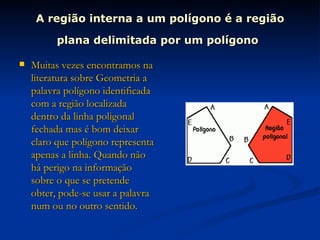
1) O documento descreve os conceitos básicos de polígonos e suas propriedades geométricas. Define polígono como uma figura formada por segmentos de reta fechados e não colineares.
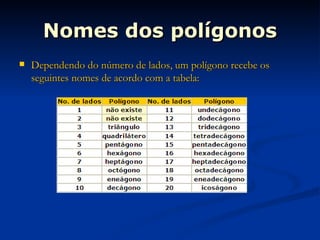
2) Apresenta as definições de região poligonal convexa e não convexa, e lista os nomes dos polígonos de acordo com o número de lados.
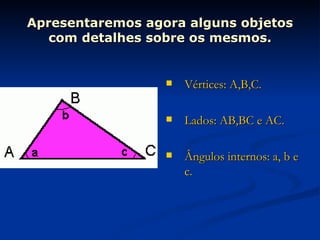
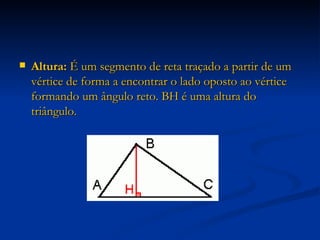
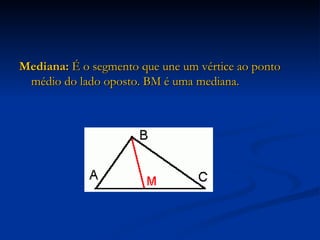
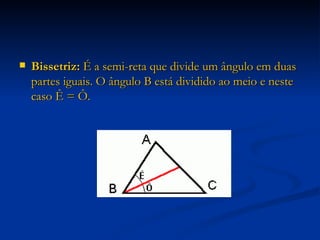
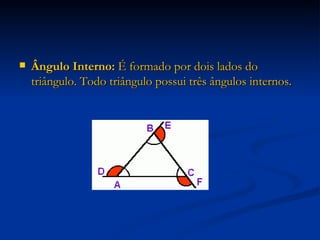
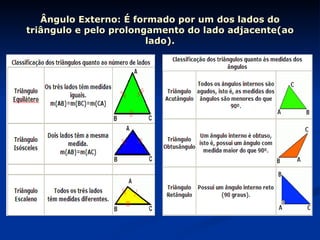
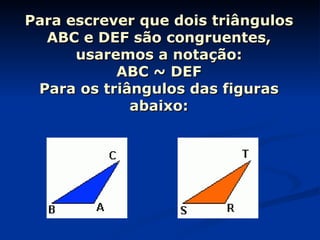
3) Detalha os elementos constituintes de triângulos, como vértices, lados, ângulos, e apresenta casos de congruência de triângulos.